Математический курс начальной школы носит название «Арифметика», так как
наиболее точно отражает содержание программы. Арифме́тика — раздел математики — раздел математики, изучающий числа — раздел математики, изучающий числа и действия с ними. В арифметике рассматриваются измерения,
вычислительные операции
(сложение (сложение, вычитание (сложение, вычитание, умножение (сложение, вычитание, умножение, деление) и приёмы вычислений. Именно арифметика наиболее полно отражает программу начальной школы.
В классической методике всегда преподавание велось предметно, и в том числе математика была разделена на предметы: арифметика в начальной школе, алгебра, геометрия, тригонометрия в средних и старших классах.
Слайд 8
Учебные пособия :
Учебник Арифметика, авторы: Александр Спиридонович Пчёлко,
Георгий Борисович Поляк
Методическое пособие по Арифметике для учителя
Счетные палочки
Бруски
– десятки
Нумерационные таблицы
Счетный пенал
Набор магнитных картинок
Дощечка, мел, тряпочка
Слайд 10
Основные разделы
программы :
1. Нумерация и 4 действия
над целыми отвлеченными числами
2. Четыре действия над именованными числами
3. Понятия о дроби и действия с дробными числами
4. Сведения из практической и наглядной геометрии
5. Текстовые задачи
Материал по нумерации и действия с целыми отвлеченными числами расположен концентрически.
При таком расположении арифметического материала понятия, даваемые учащимся в каждом концентре, имеют ту степень отвлечённости и общности, которая соответствует возрастному развитию детей. При этом каждый концентр, давая ребёнку новые знания, охватывает вместе с тем все предыдущие ступени. Благодаря этому ученик возвращается к одному и тому же понятию неоднократно и овладевает им сознательно и прочно.
Слайд 11
Концентры:
1) Счет, сложение и вычитание
до 10.
2) Нумерация, все действия в
пределах 20.
3) Действия с круглыми десятками.
4) Нумерация, действия в пределах 100.
5) Нумерация, действия до 1000.
6) Нумерация, все действия с многозначными числами.
В 1 классе - 1,2,3 концентр,
во 2 классе - 4 концентр,
в 3 классе - 5,6 концентр и
6 концентр – 4 класс
внимание уделяется устному счету, отдельно изучаются разнообразные приёмы устного
счета. Дети смело оперируют в уме с несколькими трехзначными числами, что чрезвычайно расширяет пространство ума, делает его глубоким, дает навык удерживать сразу несколько слоев информации и оперировать ими.
Устный счет, 1 класс
Учитель пишет заранее на доске примеры
9 – 1 7 – 4 7 – 6 9 – 5 10 – 4
5 + 2 6 + 2 10 – 8 2 + 7 8 – 3
Сначала учитель предлагает детям найти примеры с ответом 1, затем с ответом 2, затем с ответом 3 и так далее
Устный счёт, 2 класс
На доске заранее записаны цепочки примеров
32 + 28 – 47 + 87 – 69 =
27 + 33 – 24 + 14 – 28 =
100 – 48 + 48 – 45 + 16 =
Дети быстро считают в уме и говорят ответ примеров.
Желательно на уроках использовать игры «Лесенка», «Молчанка», «Занимательный квадрат», «Круговые примеры», «Задуманное число».
Слайд 15
Есть другие цепочки, где используются
все действия
54 : 9
36 + 28
+ 14 : 8
х 3 х 5
- 27 - 17
------ -------
( 33) ( 23)
Принцип решения этих цепочек такой же.
Устный счет развивает внутреннее внимание, мышление, глубину ума.
Когда мы производим вычисления в уме , нам нужно:
1) выбрать самый рациональный прием счета
2) удерживать в уме промежуточные результаты
3) выдать окончательный результат
Все это происходит быстро и одновременно. Работа идет на нескольких уровнях сразу.
Например, 354-182 (172)
(35-18=17 десятков , 4-2=2, можно округлить до 200)
Сравните работу ума, если я это делаю в столбик. Считаем в пределах 10 или 20.
16х25
16х100:4=1600:4=400
Слайд 17
Научить детей решать задачи –

одна из главнейших целей преподавания арифметики. Эта цель может
быть достигнута в результате плановой, глубоко продуманной, методически правильной работы по развитию этого навыка.
Одним из основных факторов, определяющих успешность обучения решению задач, является подбор задач в строго методической последовательности. Место каждой задачи в учебнике А. С. Пчёлко точно выверено и способствует успешному усвоению задач нового типа и закреплению ранее пройденных. В данном учебнике представлена комбинированная система расположения задач. Сущность ее заключается в том, что при первичном ознакомлении учащихся с новым типом подбираются однородные задачи, решаемые подряд, с тем чтобы учащиеся могли уяснить зависимость между величинами, понять способ решения. Затем для решения берутся задачи, расположенные в смешанном порядке и представляющие собой различные вариации и сочетания встречавшихся ранее видов. В учебнике А. С. Пчёлко трудным задачам предшествует ряд вспомогательных задач.
Для успешного решения задач нужно обладать некоторым математическим
развитием, уметь элементарно мыслить, анализировать условия задачи, синтезировать отдельные элементы задачи, сравнивать, сопоставлять данные, делать простейшие умозаключения. Недостаточное развитие мышления часто является причиной плохого решения задач; при этом всегда нужно помнить, что если для решения задачи требуется известный уровень развития математического мышления, то в свою очередь решение задач является самым мощным, самым действенным средством развития логического мышления. Цель и средство здесь своеобразно переплетаются между собой.
В решении задач большую роль играет и воображение. Для сознательного решения задачи нужно, чтобы учащийся понимал условие задачи и правильно представлял в своем воображении все, о чем говорится в задаче. Не менее важное значение при решении задач имеет внимание и настойчивость в преодолении трудностей.

начать решение задачи, необходимо провести разбор задачи. Из разбора
вытекает план решения задачи. Составить план – это значит наметить порядок, последовательность решения тех простых задач, на которые в результате анализа разбита сложная задача. При составлении плана окончательно формулируются вопросы каждой простой задачи, устанавливается тот порядок, в котором должны решаться одна за другой эти простые задачи.
Полезно составлять план решения не части задачи, а всей задачи от начала до конца, от первого до последнего вопроса. Ученик только тогда будет решать задачу сознательно и уверенно, когда для него ясен весь путь решения, когда ему видны все вехи на этом пути.
Для усвоения условия задачи надо прибегать к наглядным пособиям, к иллюстрированию текста задачи рисунком, картинкой или инсценированию задачи. Наглядность заставляет живее работать воображение учащихся, она развивает у детей способность связывать прочитанные слова с их конкретным содержанием; под воздействием наглядности у детей возникают нужные образы.
– это умение решать задачи.
Задача , 1 класс,
4 урок
Предварительная беседа обязательна.
- Кто из вас помогал родителям или бабушкам и дедушкам убирать на огороде овощи? Когда убирают овощи?
Учитель вызывает ученика, ставит перед ним корзинку. На столе приготовлено несколько морковок.
- Сейчас будешь класть морковь в корзинку. А вы, дети смотрите и слушайте, что я буду говорить.
- Положи в корзинку 2 морковки
Ученик отсчитывает 2 морковки , показывает их классу и кладёт в корзинку.
- Положи в корзинку ещё одну морковку. Ученик выполняет задание.
- Сколько всего морковок ты положил в корзинку?
В это период обучения очень часты случаи, когда дети не дожидаясь конца вопроса в задачах, выкрикивают с места ответ.
Необходимо объяснить и научить, как повторять условие задачи, как отвечать полным ответом на вопрос задачи. ( Причем, термины – условие и вопрос задачи учитель не использует!)
Слайд 22
Задача №233, 1 класс, урок 81 ( Задача
на нахождение остатка)
- Кто из вас
был на зимней рыбалке? Как рыбачат зимой?
Чтение и показ задачи:
Рыбак поймал 18 рыб, из них – 8 окуни, остальные караси. Сколько карасей поймал рыбак?
Рыбы можно магнитами прикрепить к доске.
- Сколько рыб поймал рыбак?
( Ответ детей должен быть полным : Рыбак поймал 18 рыб.)
- Сколько окуней поймал рыбак? ( 8 окуней поймал рыбак)
- Как сосчитать сколько карасей поймал рыбак?
- Запишем решение задачи, может один ученик диктовать , учитель записывает на доске)
№233
18 р. – 8 р. =10 р.
Ответ : 10 карасей поймал рыбак.
Уточнить, что именно карасей – 10 ( показать)
Дети записывают задачу в тетрадь и проговаривают ответ задачи.
Задачи в учебнике расположены очень интересно.
Задачи расклассифицированы, с целью постепенного усложнения.
Слайд 23
3 класс, с.85 №691
В пруд выпустили рыбу для
разведения. Карпов выпустили 1352, карасей в два раза меньше, чем карпов, а окуней - на 48 меньше, чем карасей. Сколько рыб выпустили в пруд?
Кто ходил на рыбалку и ловил рыбу ? – включаем воображение
Посмотрим на иллюстрацию
Читаем дважды, перескажи о чем задача, числа запоминать не нужно (если ребенок пересказал, он усвоил)
Краткая запись не всегда нужна – нельзя тормозить мышление ребенка, краткая запись – помощь, не рубите мысль
Понятная краткая запись
Карпы – 1352 р.
Караси – в 2 раза меньше, чем карпов
Окуни – на 48 рыб меньше, чем карасей
Сколько рыб всего?
Решение задачи
Слайд 24
Разберем задачу аналитически –
отталкиваемся от вопроса
Сколько всего рыб?
Что нужно знать , чтобы ответить на этот вопрос – сколько карпов, карасей, окуней. Сколько карпов мы знаем, сколько карасей и окуней.
Синтетический – от условия. Что мы знаем про карасей?
Чаще в 1 и 2 классе
Анализ не всегда применим
Запись решения.
Вопросы плана лучше, чем пояснения
Сколько выпустили карасей?
1352р.:2=676р.
Сколько выпустили окуней?
676р. – 48 р. = 628 р.
Сколько всего выпустили рыб?
1352р. + 676 р. + 628 р. = 2656р.
Ответ : 2656 рыб выпустили в пруд.
Слайд 26
Работа с нумерационными таблицами.
Демонстрация таблиц
В 1 классе
работают с таблицей 1 разряд единиц и 2 разряд
десятков 1 класса
К концу 1 класса появляется таблица – 3 разряд сотни
Слайд 28
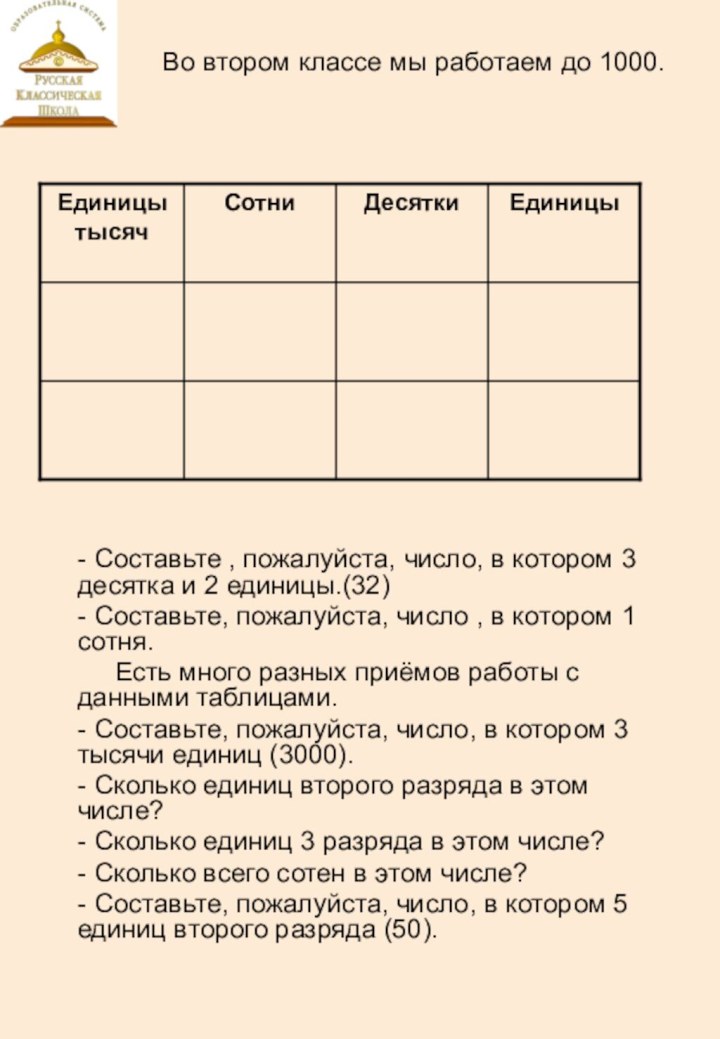
- Составьте , пожалуйста, число,
в котором 3 десятка и 2 единицы.(32)
- Составьте, пожалуйста, число , в котором 1 сотня.
Есть много разных приёмов работы с данными таблицами.
- Составьте, пожалуйста, число, в котором 3 тысячи единиц (3000).
- Сколько единиц второго разряда в этом числе?
- Сколько единиц 3 разряда в этом числе?
- Сколько всего сотен в этом числе?
- Составьте, пожалуйста, число, в котором 5 единиц второго разряда (50).
Во втором классе мы работаем до 1000.
Слайд 30
Переходим к формированию вычислительных навыков.

Как же можно добиться
осознанных, крепких вычислительных навыков? Все, что мы объясняем детям должно быть ими понято и осознанно. Это можно сделать с помощью счетного материала, с помощью наглядности на конкретном действенном опыте можно вместе с детьми проникать в глубинную сущность действий и явлений.
Сложение с переходом через десяток.
Для изучения данной темы на партах у детей 2 бруска – десятка палочки 1 десяток красного цвета, другой десяток – синего цвета.
- Посчитайте, сколько дырочек в каждом бруске?
(10)
- Эти бруски называют бруски – десятки. Положите перед собой 8 синих палочек и 6 палочек красного цвета.
Пример: 8 + 6 =
Возьмите один брусок и аккуратно вставьте 8 синих палочек. Теперь в этот же брусок добавьте красные палочки.
- Сколько палочек удалось нам добавить в брусок?
(2)
- Сколько палочек получилось в этом бруске? ( 10)
- Сколько красных палочек надо было прибавить ? (6)
- А сколько осталось ещё красных палочек на парте? (4)
- Вставьте эти палочки во второй брусок.
- Сколько палочек получилось в двух брусках? (14)

Понятие о
десятке и единице
– Достаньте свои палочки и пересчитайте их. Сколько у вас палочек? (10.) Давайте свяжем их в пучок резинкой.
Учитель отсчитывает свои 10 палочек и завязывает их резинкой в пучок. Дети проделывают то же самое.
– Сколько палочек в вашем пучке? (10 палочек.) Число 10 ещё называется десятком. Возьмите в руки ваш десяток, как мы набирали его? (По одной палочке.)
Учитель, держа в одной руке свой пучок-десяток, в другую берет 1 палочку и говорит:
– Одну палочку будем называть единицей. Сейчас я вам раздам ещё по 10 палочек-единиц.
Раздает всем ученикам ещё по 10 палочек.
– Покажите связанные в пучок 10 палочек. Как назвать их иначе? (Десяток.)
– Покажите 1 палочку. Как сказать иначе? (Единица.)
– Мама купила десять яиц. Сколько яиц она купила? Как сказать иначе? (Десяток яиц.)
– Что еще можно считать десятками? (Пуговицы, конфеты, тетради, яблоки… Всё, чего много, можно считать десятками.)
– Теперь достаньте ваши кубики, пересчитайте их. Сколько кубиков вы насчитали? (10.) Заменим эти кубики-единицы на брусок-десяток из кубиков (раздать бруски). Пересчитайте кубики в бруске – их тоже 10, десяток.
– Теперь у вас есть пучок-десяток из палочек и палочки-единицы, и брусок-десяток из кубиков и кубики-единицы. Мы на уроках теперь будем с ними работать.
Слайд 32
2) Образование чисел второго десятка на классных пособиях.
– Приготовьте для работы брусок-десяток и кубики-единицы. В прошлом
десяток назывался «дцать».
Положите перед собой ваш брусок-десяток, возьмите один кубик и положите его сверху на десяток. Скажите: «Кладу ОДИН НА ДЦАТЬ, получилось число один-на-дцать». Произнесите еще раз.
– Возьмите 2 кубика и положите сверху на десяток, скажите: «Кладу ДВА НА ДЦАТЬ или ДВЕ НА ДЦАТЬ, получилось число две-на-дцать» (и так же проработать каждое число второго десятка).
– Три-на-дцать.
– Четыр-на-дцать. (Удобнее ли стало называть числа, когда они стали короче? Попробуйте произнести так, как было сначала, и так, как стало сейчас, – как вам удобнее?)
– Пят-на-дцать.
– Шест-на-дцать.
– Сем-на-дцать.
– Восем-на-дцать.
– Девят-на-дцать.
– А теперь получилось 2 полных десятка, у нас был один «дцать», а теперь два «дцать» – двадцать.
внимание – ребенок обязательно должен действовать и видеть. Без
счетного материала эта работа не имеет такого влияния, как в данном случае – конкретные действия, которые выполняет сам ребенок.
Умножение.
Тоже имеет свои особенности по классической методике. Например, по 4 кубика взять 3 раза. Я должна брать по 4 кубика. На первых этапах работы с умножением не говорят 4 умножить на 3, а говорят – по 4 взять 3 раза, потому что эта фраза для ребенка понятнее и легче, а фраза 4 умножить на 3 для него пока смысла не несет и только потом будет переход к действию умножения. Мы различаем для детей начальной школы множимое и множитель.
Слайд 35
Таблица умножения может быть построена двумя
способами :
1) по постоянному множимому
2) по
постоянному множителю
4х2=8 2) 2х4=8
4х3=12 3х4=12
4х4=16 4х4=16
4х5=20 5х4=20
Учитель по очереди вызывает 4 учеников и предлагает первому ученику взять со стола два раза по две тетради. Ученик берет первый раз 2 тетради и говорит : «Я взял 2 тетради один раз». Тетради выставляются на планку классной доски. Берет во второй раз две тетради , говорит: «Я взял ещё 2 тетради» и ставит их на небольшом расстоянии от первых.
- Сколько раз ты взял по две тетради?
- «Я взял по тетради два раза»
Слайд 36
Второму ученику дается задание взять 3
раза по две тетради, третьему ученику – взять 4
раза по 2 тетради, последнему – 5 раз по две тетради.
Умножение и деление целесообразно изучать раздельно, рассмотрев сначала все случаи умножения и только после этого переходить в делению.
Деление.
Виды деления – по содержанию, на
равные части.
Положите перед собой 15 палочек. Попробуйте эти 15 палочек разделить на 3 равные части.
15 палочек :3= 5 палочек
На равные части (делим по 1)
Положите перед собой 15 палочек и поделите их по 3 палочки на части (кучки)
15 палочек:3 палочки=5
Деление по содержанию (делим по 3)
Сначала детям дается деление на равные части, затем деление по содержанию, а затем дается сравнение 2 видов деления.
В учебнике 2 класса на странице 52 Задачи про вишни.
Слайд 38
Сначала детям дается деление на равные
части, затем деление по содержанию, а затем дается сравнение
2 видов деления. В учебнике 2 класса на странице 52 есть задача про вишни.
Задача 1 ( на равные части)
Дети разложили 12 вишен поровну в 3 вазочки. Сколько вишен положили в каждую вазочку?
12 в. : 3 = 4 в.
Ответ: 4 вишни положили в каждую вазочку.
Слайд 39
Задача 2 ( по содержанию)
Дети
разложили 12 вишен в вазочки по 4 вишни в
каждую. Сколько понадобилось вазочек?
12 в. : 4 в. = 3 вазочки
Ответ : 3 вазочки понадобилось.
При решении задач очень важно постоянно делать акцент на правильность записи наименований
Слайд 40
Сложение.
Это происходит в 3 классе.
Мы даем алгоритм, который должен будет точно понят и
осознан.
Видео «Методика обучению письменному сложению»
Первоначально даются задачи и примеры без перехода через десяток. И ребенку всё очень просто и понятно. Далее вводятся примеры, где есть только переход единиц в единицах. Следующий этап изучения темы – переход десятков. И завершающий этап – это переход через десяток и единицы.
С заботой о ребенке в строгой логической последовательности выстроен весь материал.
Вычитание
Видео
«Методика обучению письменному вычитанию»
Аналогично сложению идёт подача материала письменного вычитания.
Первоначально вычитаем
286-123
345-128 дробим десяток
426-165 дробим сотню
425-148 дробим и сотни, и десятки
506-135 на месте десятков 0
Действия с
именованными числами.
Перед тем как работать с именованными числами, необходимо познакомить детей с мерами, над которыми мы будем производить действия.
Точно также мы активно используем наглядность для знакомства с мерами.
Кг – подержим в руке, по взвешиваем.
М – отмерим.
Меры площади – нарисуем.
Квадратный см, м, ар, га – выездные занятия.
У детей должны быть сформированы четкие представления об этих мерах.
Меры объема – наглядность. см³ , м³
Почему дети путают площадь и объем, оттого что все эти меры не проработаны, не прожиты ими , не представляют они.
Видео «Меры объема 4 класс»
После подобной практической работы все таблицы мер будут запомнены особенно.
Запись – кубические см, квадратный см.
Сначала действия с метрическими мерами, потом с мерами времени, так как они сложнее.
Видео «Именованные числа 4 класс»
Слайд 45
Программа по арифметике для II класса
насыщена важным и сложным материалом. Здесь у детей закладываются
фундаментальные основы устного счёта: учащиеся усваивают характерные приёмы устных вычислений. На протяжении этого года обучения дети должны овладеть следующими математическими понятиями: увеличение и уменьшение числа в несколько раз, разностное и кратное сравнение, нахождение доли, два вида деления ( деление по содержанию и деление на равные части), все виды сложения и вычитания в пределах 100, табличное и внетабличное умножение и деление; научиться решать простые и сложные задачи, а также задачи, выраженные в косвенной форме.
Слайд 46
Текстовые задачи
Они являются и целью и средством обучения математики.
Им посвящается много времени. На задачах мы разъясняем новый материал, также осуществляем связь с жизнью, с практикой.
Задачи расположены очень интересно.
Задачи расклассифицированы, с целью постепенного усложнения.
С классификацией задач можно познакомиться в книжке Поляк «Обучение решению задач в начальной школе». Здесь приведена полная классификация всех задач, которые встречаются в курсе арифметики
Слайд 47
Значительно расширяются знания детей II класса и в
области измерений. Здесь учащиеся знакомятся с километром и граммом,
усваивают меры времени: год, месяц, число дней в каждом месяце, сутки, час, минута. Здесь они практически знакомятся с прямоугольником и квадратом и измерением их сторон.
Во II классе дети начнут решать задачи на движение. Чем раньше они приобретут практический опыт измерения расстояний, нахождения времени, вычисления скорости; поймут прямую и обратную взаимозависимость этих величин, тем более осознанно и легко они будут решать задачи на движение.
Слайд 48
В III классе дети освоят все приёмы письменных
вычислений, однако при этом необходимо не снижать количество и
качество устных вычислений, предотвращая замену устных вычислений письменными. Желательно соблюдать связь между темой урока и упражнениями в устных вычислениях, делая занятия устным счётом целенаправленными.
При изучении геометрического материала рекомендуется пользоваться разнообразными наглядными пособиями.
Слайд 49
Программный материал IV класса обширен и разнообразен по
содержанию. Значительную часть курса составляет раздел именованных чисел. Чтобы
безошибочно производить с ними вычисления, учащиеся должны получить ясные представления о действительной величине мер, научиться пользоваться ими, наработать навыки измерения и взвешивания, развить глазомер. Свободное и осознанное оперирование с именованными числами – важнейший фундамент для последующего изучения таких наук, как физика и химия.
Несмотря на то, что дети уже владеют всеми приёмами письменных вычислений, в IV классе мы продолжаем заниматься систематическим устным счётом.
Во второй и третьей четвертях часть времени отводится на изучение геометрического материала. Дети должны получить практические навыки в измерении и вычислении площадей и фигур, имеющих форму прямоугольника и квадрата, научиться вычислять объёмы тел, имеющих прямоугольную форму.
Слайд 50
Последней большой темой начальной школы является тема «Обыкновенные
дроби», где дети получают первое представление о долях, дробях,
их величине, максимально используя наглядные пособия.
Большое внимание будет уделено решению задач. В IV классе наряду с задачами, которые изучили в III классе, решаются новые задачи: на нахождение среднего арифметического нескольких чисел, на определение чисел по сумме и кратному отношению, на нахождение одной или нескольких частей числа, на применение способа отношений.