Слайд 2
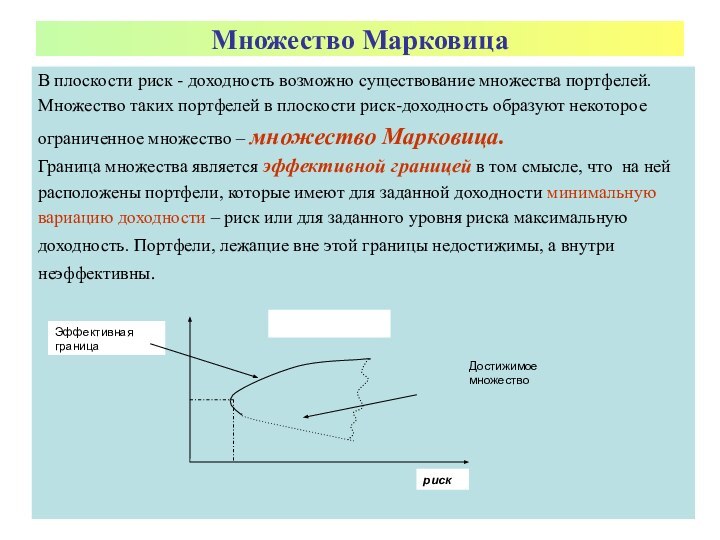
Множество Марковица
В плоскости риск - доходность возможно существование
множества портфелей.
Множество таких портфелей в плоскости риск-доходность образуют
некоторое
ограниченное множество – множество Марковица.
Граница множества является эффективной границей в том смысле, что на ней
расположены портфели, которые имеют для заданной доходности минимальную
вариацию доходности – риск или для заданного уровня риска максимальную
доходность. Портфели, лежащие вне этой границы недостижимы, а внутри
неэффективны.
Достижимое множество
Эффективная граница
Слайд 3
Множество Марковица
Модель Марковица основана на следующих предположениях.
Рынок состоит
из конечного числа абсолютно ликвидных активов.
Доходности являются нормально распределенными
случайными величинами, имеющие конечные значения математического ожидания (доходности ) и дисперсии (риск).
Индивидуальные предпочтения инвестора определяются функцией полезности от двух аргументов – ожидаемой доходности и и риска.
Инвесторы не склонны к риску. Инвестор при одинаковых доходностях предпочитает портфель с меньшим риском или при одинаковых рисках инвестор предпочитает портфель с большей доходностью.
Налоги и транзакционные издержки отсутствуют.
Слайд 4
Эффективный портфель
Портфель, который имеет наименьший риск при заданной
доходности, или максимальную доходность при заданном риске называется эффективным.
Слайд 5
Эффективная граница
С математической точки зрения нахождение эффективной границы
- это
задача оптимизации. Требуется найти доли ценных бумаг,
при которых
для заданного уровня доходности риск (вариация) портфеля будет
минимальной.
Если необходимо сформировать эффективный портфель из N бумаг, то
для ее решения применяется метод квадратичного программирования
или метод множителей Лагранжа.
Для решения задачи об инвестировании необходимо иметь следующую
информацию:
Ожидаемые доходности ценных бумаг из которых предполагается формировать портфель,
риск (стандартное отклонение доходности) каждой ценной бумаги, матрицу вариаций ковариаций (фактически ковариацию каждой пары бумаг)
Слайд 6
Эффективная граница
Для математической формулировки задачи оптимизации удобно записать
ее в матричном виде. Используя введенные ранее обозначения для
вариации портфеля
Целевая функция при введении множителей приобретает вид
Для трех акций лангранжиан равен
Слайд 7
Эффективная граница
Условие минимума означает выполнения равенства частных производных
L
первого порядка. Значение второй производной автоматически больше нуля,
поскольку вариация Var(rp) является выпуклой функцией долей.
Решая задачу для трех активов в результате получим систему из пяти линейных
уравнений
Слайд 8
Эффективная граница
В матричном виде система уравнений имеет вид
=
Обозначим матрицу вариация -доходность как VCV1, вектор содержащий
доли и
множители Лагранжа, который необходимо найти, как W1, а вектор доходностей
справа, как А, то уравнение в матричном виде запишется как
VCV1*W1=А
Решение этого уравнения в матричном виде имеет вид
Слайд 9
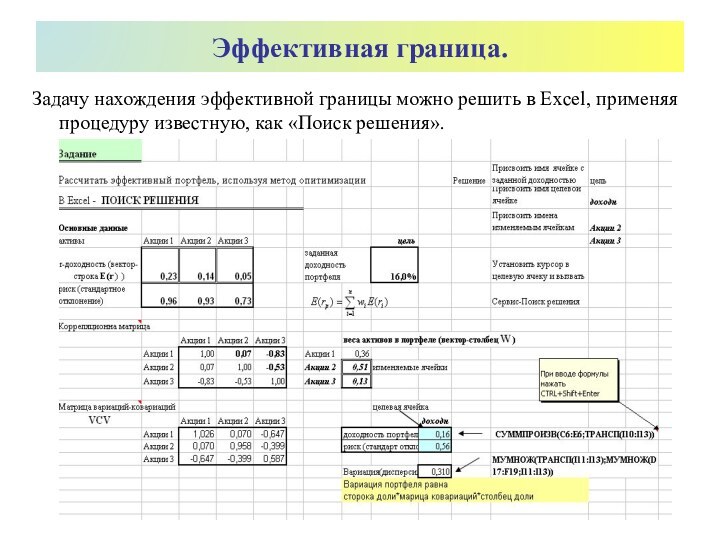
Эффективная граница.
Задачу нахождения эффективной границы можно решить в
Excel, применяя процедуру известную, как «Поиск решения».
Слайд 10
Эффективный портфель из N активов
Слайд 11
Задача с запрещенной короткой позицией
Все веса должны
быть неотрицательны. Условия для нахождения эффективного портфеля с разрешенной
короткой позицией имеют вид
целевая функция
при ограничениях
Слайд 12
Задача с запрещенной короткой позицией
Для лагранжиана задача при
запрещенной короткой позиции имеет вид
Задача решается численно.
Слайд 13
Пример. Пусть на рынке имеются три акции. Доходности,
стандартное отклонение ковариация даны ниже в таблице
Найти эффективный
портфель, имеющий доходность 16%.
Решение методом множителей Лагранжа.
Доходность рассчитаем по формуле
Риск по формуле
Слайд 14
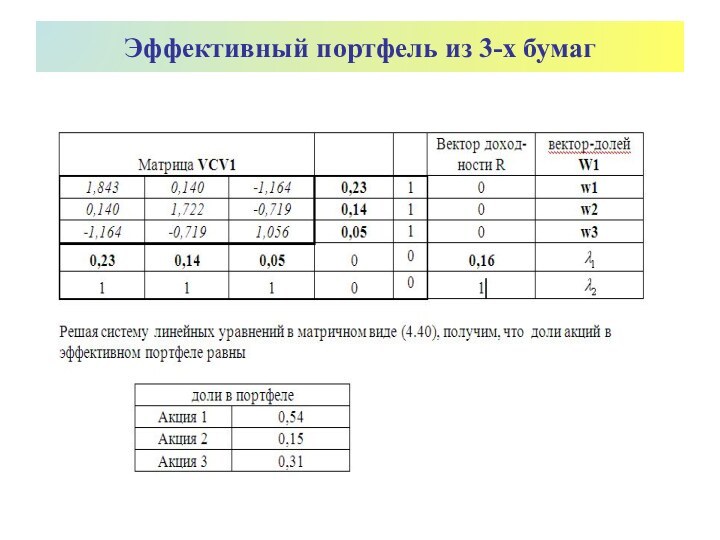
Эффективный портфель из 3-х бумаг
Слайд 15
Портфель из двух активов.
Риск и доходность портфеля из
двух бумаг легко находится из формул
Поскольку сумма весов в
портфеле должна быть равна единице, то выразим вес акции 2 через вес акции (1 - 1 ); 2 = 1 - 1
Слайд 16
Эффективный портфель из двух бумаг
Приравнивая производную от дисперсии
к нулю получим
Доля первого актива равна
Минимальный риск будет при
корреляции равной
Слайд 17
Эффективный портфель из двух бумаг
Доходность при равна
при
коэффициенты
соответственно равны
При этом, если , то и наклон положительный
При наклон отрицательный.
Слайд 18
Для
Коэффициент В как правило положителен, поскольку большей
доходности соответствует больший риск. Уравнения задают множество портфелей в
зависимости от коэффициента коррелляции в неявном (параметрическом ) виде
Слайд 19
Эффективный портфель из двух бумаг
Слайд 20
Оптимальный портфель
Для инвестора оптимальный портфель – это
портфель, который находится на точке касания кривых безразличия инвестора
и границы эффективного множества Марковица
Соотношение риска и ожидаемой доходности инвестиции для инвестора описывается функцией полезности или функцией предпочтений инвестора, которая характеризует отношение инвестора к получению прибыли в условиях неопределенности.
Теория полезности основывается на том, что в условиях неопределенности получения будущих доходов, даже при наличии количественных оценок риска, инвесторы считают, что большей полезности (доходности) отвечает большая неопределенность (риск).
Слайд 21
Функция полезности.
Функция полезности связана с неопределенностью получения будущих
доходов имеет вид
Два вида функции полезности:
квадратичная (классическая).
логарифмическая (функция
полезности Марковитца
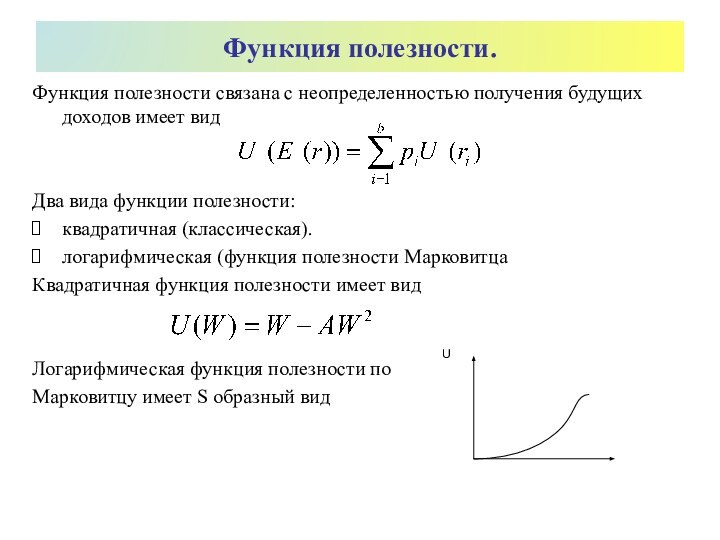
Квадратичная функция полезности имеет вид
Логарифмическая функция полезности по
Марковитцу имеет S образный вид
Слайд 22
Функция полезности.
В терминах ожидаемой доходности квадратичная функция полезности
имеет вид
Поскольку доходность – это случайная величина, которая
является нормально распределенной величиной, то для ожидаемой полезности получим
Для инвестора оптимальный портфель – это портфель, который находится на точке касания кривых безразличия инвестора и эффективного множества Марковитца