- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Модели для рынка ценных бумаг. (Лекция 4)
Содержание
- 2. Введение в управление портфелем ценных бумаг
- 3. бумаг.
- 4. 1. Построение Markowitz Model для российского рынка ценных бумаг
- 5. Г. Марковиц в 1952 году предложил математическую
- 6. Портфель – это совокупность финансовых активов, объединенных
- 7. Так же доходность портфеля будет выглядеть как
- 8. Экономико-математическая модель задачи формирования оптимального портфеля акций максимальной эффективности
- 13. В модели Г. Марковица риск отдельно взятого
- 16. 2. Модель CAPM (Capital Assets Price Model)Модель
- 17. Формула Sharpe связи будущей доходности ценной бумаги
- 18. Ожидаемая норма доходности – эта та доходность ценной
- 19. Пример применения модели оценки капитальных активов –
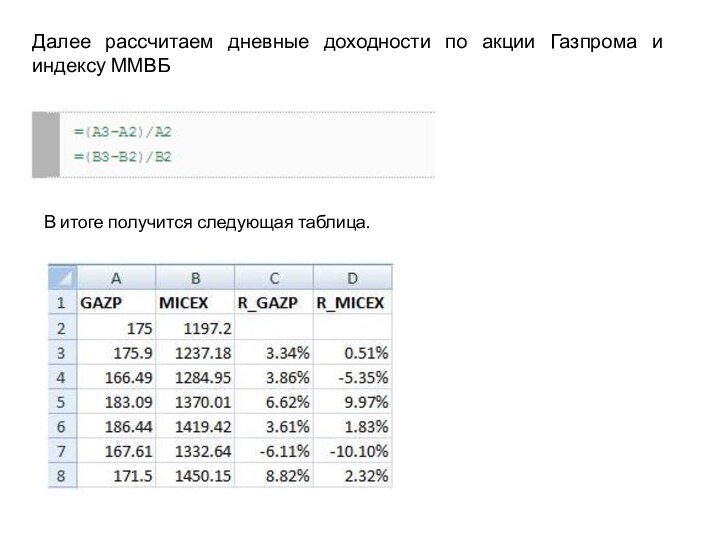
- 20. Далее рассчитаем дневные доходности по акции Газпрома и индексу ММВБВ итоге получится следующая таблица.
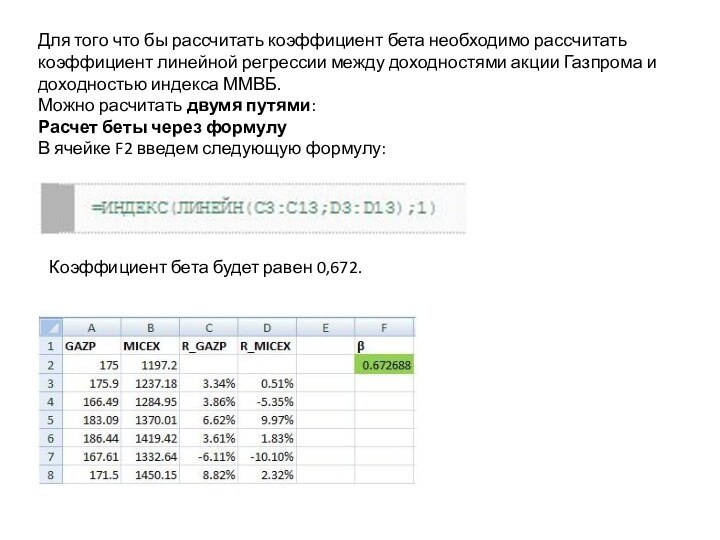
- 21. Для того что бы рассчитать коэффициент бета
- 22. Расчет беты через надстройку «Анализ данных» Для
- 23. Отчет по регрессии выглядит следующим образом. В
- 25. Осталось рассчитать месячную доходность рынка, доходность индекса
- 26. Мы рассчитали все необходимые параметры модели CAPM.
- 27. 3. Модель ШарпаФормирование инвестиционного портфеля на основе
- 28. Рыночный индекс включает в себя взвешенный набор различных
- 30. Наш портфель будет состоять из 4 акций: Газпрома (GAZP),
- 31. После этого создадим колонку со значениями нашего
- 35. 4. Модель квази-ШарпаФормирование инвестиционного портфеля на основе
- 36. 3. Доходность ценной бумаги прямо пропорционально
- 37. Модель «Квази – Шарпа» соединяет доходность ценной бумаги
- 38. Необходимо сказать несколько слов об измерении риска
- 39. Риск же рассчитывается по следующей формуле:Задача формирования оптимального портфеля
- 40. Обратная задача формирования оптимального портфеля, где мы
- 42. Следующим этапом рассчитаем доходности этих акций по следующей формуле:Где:
- 43. И аналогично рассчитываем доходности всех акций. На рисунке
- 45. Далее рассчитаем доходность единичного портфеля. Сделав необходимые расчеты,
- 46. В Excel расчет доходностей единичного портфеля (ЕП) будет выглядеть следующим образом:
- 47. Далее рассчитаем чувствительность изменения доходности акции от изменения доходности
- 48. Для вычисления числителя по периодам коэффициента бета
- 50. Следующим этапом рассчитаем остаточный риск, который представляет
- 51. При формировании инвестиционного портфеля из этих акций
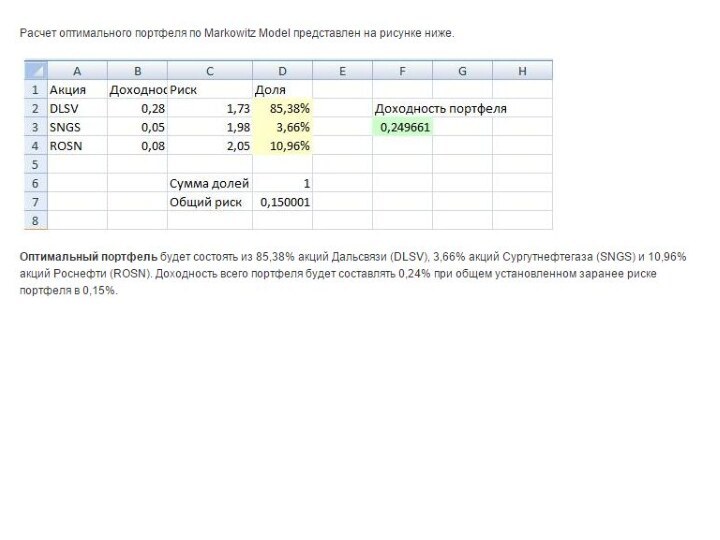
- 52. Итак, давайте обобщим все полученные данные в
- 54. Формула расчета целевой ячейки с доходностью портфеля
- 56. В итоге мы получаем расчет долей акций
- 57. Скачать презентацию
- 58. Похожие презентации


































Слайд 5 Г. Марковиц в 1952 году предложил математическую модель
формирования инвестиционного портфеля. В основе его модели лежат два
ключевых показателя любого финансового инструмента: доходность и риск, которые были количественно измерены. Доходность по модели представляет собой математическое ожидание доходностей, а риск определяется как разброс доходностей возле математического ожидания и рассчитывается через стандартное отклонение.Выделяют две инвестиционные стратегии при формировании портфеля:
► Максимизации доходности инвестиционного портфеля при ограниченном уровне риск.
► Минимизация риска инвестиционного портфеля при минимально допустимом уровне доходности.
Слайд 6 Портфель – это совокупность финансовых активов, объединенных вместе
для реализации целей инвестора, для максимизации прибыли и минимизации
убытков.В Markowitz Model допустимыми являются только стандартные портфели, портфели без коротких позиций (без продаж), то есть портфель, состоящий только из купленных акций.
Отсюда первое ограничение, которое накладывается на портфель, это положительные доли всех ценных бумаг (хi).
Второе ограничение состоит в том, что сумма всех долей ценных бумаг должна составлять 1, это правило нормировки долей. Формула показывает это ограничение:
Слайд 7 Так же доходность портфеля будет выглядеть как сумма
доходностей отдельных акций с выбранными весовыми коэффициентами. Так как
каждый инвестор пытается максимизировать получаемую доходность, то необходимо будет максимизировать эту целевую функцию. В итоге это будет выглядеть в виде формулы:Помимо доходности инвестору необходимо так же учесть и риск, связанный с той или иной акцией.
Риск по Markowitz выражается в виде среднеквадратического отклонения δi каждой акции. Значение δр – это уровень приемлемого риска для инвестора. Помимо учета средне квадратического отклонения отдельных акций необходимо учесть корреляцию между доходностями акций – rij . Корреляция в нашем случае для Markowitz Model равняется нулю. В итоге риск всего портфеля представлен формулой:
Слайд 8 Экономико-математическая модель задачи формирования оптимального портфеля акций максимальной эффективности при
которой риск портфеля не превышает заданного значения δр , и
при учете всех ограничений на портфель, примет следующий вид :
Слайд 13 В модели Г. Марковица риск отдельно взятого финансового
инструмента рассчитывается как стандартное отклонение доходностей. Для расчета общего
риска портфеля необходимо отразить их совокупное изменение и взаимное влияние (через ковариацию), для этого воспользуемся следующей формулой:где:
σp – риск инвестиционного портфеля;
σi – стандартное отклонение доходностей i-го финансового инструмента;
kij – коэффициент корреляции между I,j-м финансовым инструментом;
wi – доля i-го финансового инструмента (акций) в портфеле;
Vij – ковариация доходностей i-го и j-го финансового инструмента;
n – количество финансовых инструментов инвестиционного портфеля.
Слайд 16
2. Модель CAPM (Capital Assets Price Model)
Модель CAPM
(Capital Assets Price Model) предназначена для определения цены акции
или стоимости компании в будущем, другими словами, текущая оценка перекупленности или перепроданности компании.Модель CAPM часто используется как дополнение к портфельной теории Markowitz. В практике построения инвестиционных портфелей, модель CAPM, как правило, используется для выбора активов из всего множества, далее уже с помощью Markowitz Model формируется оптимальный портфель.
Модель CAPM связывает такие составляющие как будущая доходность ценной бумаги и риск этой бумаги.
Слайд 17 Формула Sharpe связи будущей доходности ценной бумаги и
риска
где:
R- ожидаемая норма доходности;
Rf – безрисковая ставка доходности, как правило,
ставка по государственным облигациям;Rd- доходность рынка;
β- коэффициент бета, который является мерой рыночного риска (недиверсифицируемого риска) и отражает чувствительность доходности ценной бумаги к изменениям доходности рынка в целом.
Слайд 18 Ожидаемая норма доходности – эта та доходность ценной бумаги,
на которую рассчитывает инвестор. Другими словами- эта прибыль этой
ценной бумаги.Безрисковая ставка доходности – эта доходность, полученная по безрисковым ценным бумагам. Как правило, берут ставку по государственным облигациям. Что бы посмотреть ставки по государственным облигациям можно зайти на сайт центрального банка РФ. http://cbr.ru/hd_base/OpenMarket.asp . В России, на данный момент, она составляет 5.04%.
Под доходностью рынка понимают доходность индекса данного рынка, в нашем случае индекс РТС (RTSI). Для Американских акций берут индекс S&P500.
Бета – коэффициент показывающий рискованность ценной бумаги.
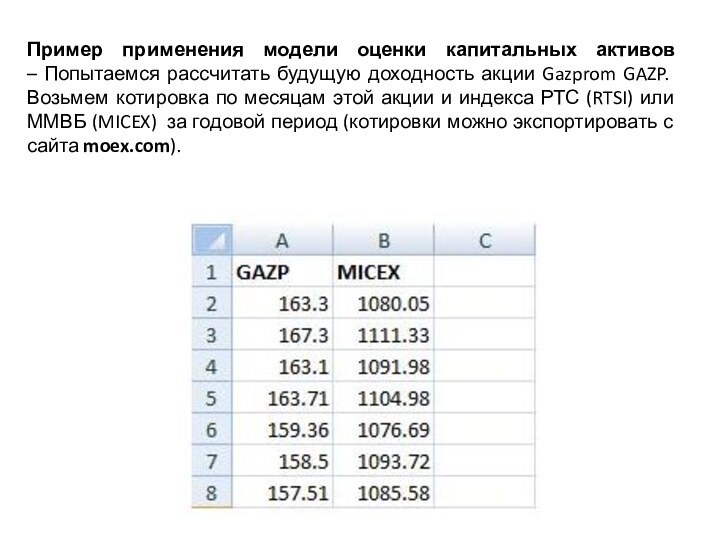
Пример применения модели оценки капитальных активов – Попытаемся рассчитать будущую доходность акции Gazprom GAZP. Возьмем котировка по месяцам этой акции и индекса РТС (RTSI) или ММВБ (MICEX) за годовой период (котировки можно экспортировать с сайта finam.ru).
Слайд 19 Пример применения модели оценки капитальных активов – Попытаемся рассчитать
будущую доходность акции Gazprom GAZP. Возьмем котировка по месяцам
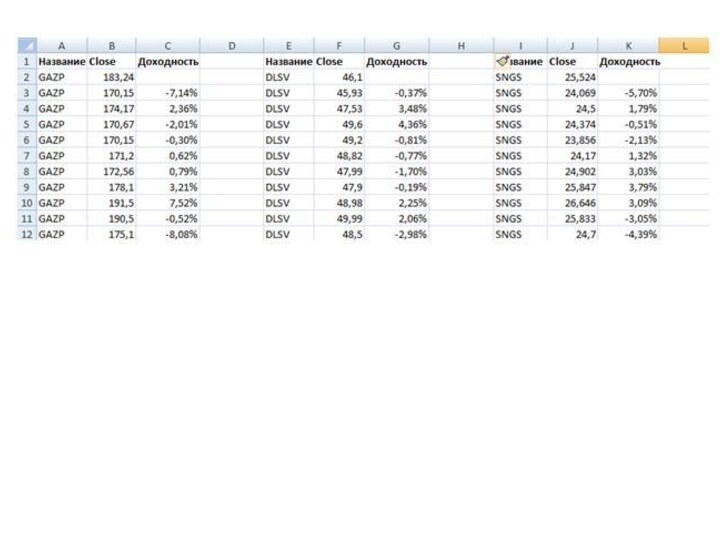
этой акции и индекса РТС (RTSI) или ММВБ (MICEX) за годовой период (котировки можно экспортировать с сайта moex.com).Слайд 20 Далее рассчитаем дневные доходности по акции Газпрома и
индексу ММВБ
В итоге получится следующая таблица.
Слайд 21 Для того что бы рассчитать коэффициент бета необходимо
рассчитать коэффициент линейной регрессии между доходностями акции Газпрома и
доходностью индекса ММВБ.Можно расчитать двумя путями:
Расчет беты через формулу В ячейке F2 введем следующую формулу:
Коэффициент бета будет равен 0,672.
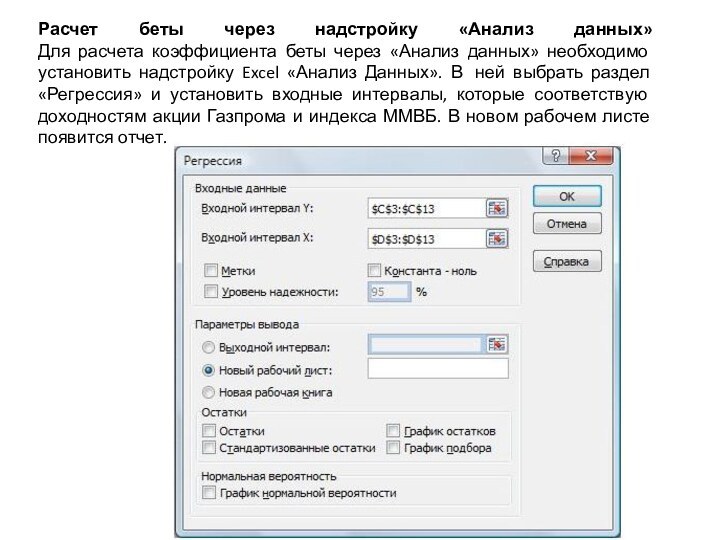
Слайд 22 Расчет беты через надстройку «Анализ данных» Для расчета коэффициента
беты через «Анализ данных» необходимо установить надстройку Excel «Анализ
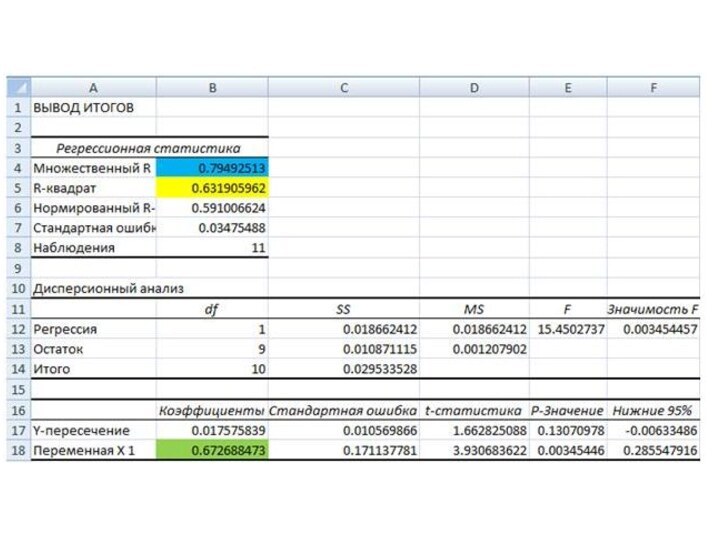
Данных». В ней выбрать раздел «Регрессия» и установить входные интервалы, которые соответствую доходностям акции Газпрома и индекса ММВБ. В новом рабочем листе появится отчет.Слайд 23 Отчет по регрессии выглядит следующим образом. В ячейке
В18 находится расчет коэффициента линейной регрессии, как раз необходимый
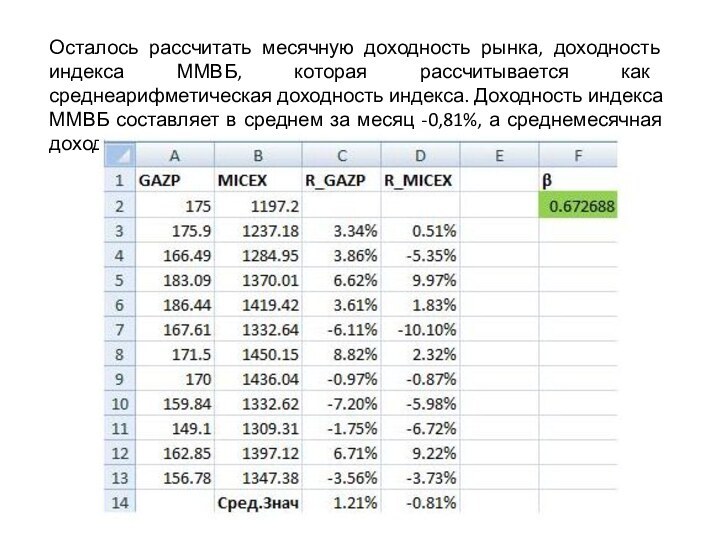
коэффициент бета. Коэффициент бета равен 0,67. Так же в отчете есть показатель R- квадрат (коэффициент детерминированности), значение которого равно 0,63. Он показывает силу зависимости меду независимыми переменными (зависимость между доходностью акции и индексом). Показатель Множественный R –является коэффициентом корреляции. Как видим коэффициент корреляции составляет 0,79, что говорит о сильной связи между доходностью индекса и доходностью акции Газпрома.Слайд 25 Осталось рассчитать месячную доходность рынка, доходность индекса ММВБ,
которая рассчитывается как среднеарифметическая доходность индекса. Доходность индекса ММВБ
составляет в среднем за месяц -0,81%, а среднемесячная доходность акции Газпрома 1,21%.Слайд 26 Мы рассчитали все необходимые параметры модели CAPM. Теперь
рассчитаем справедливую норму доходности акции Газпрома на следующий месяц.
Rf=5.04%, β=0.67, Rd=-0.81%.RGAZP=5,04%+0,67*(-0,81%-5,04%)=1,12%
Норма доходности акций Gazprom равняется 1,12% на следующий месяц. Можно сказать, что это прогнозная цена будущей доходности в следующем отчетном периоде. Модель оценки капитальных активов –инструмент оценки акций и ценных бумаг, позволяющий составить прибыльный инвестиционный портфель.
Слайд 27
3. Модель Шарпа
Формирование инвестиционного портфеля на основе метода
Sharpe index.
Существует несколько методов управления портфелем, как правило, они делятся
на два вида. Активное и пассивное управление портфелем. Активное управление портфелем состоит в поиске арбитражных возможностей для извлечения сверхприбыли из рынка. Придерживаясь этой стратегии управления, портфельный менеджер использует различные методы прогнозирования и анализа для поиска закономерностей рынка и извлечение дополнительный прибыли.Пассивное управление портфелем состоит в составлении сильно диверсифицированного портфеля для минимизации рыночного риска. Цель портфельного управляющего составить наиболее защищенный портфель от рыночных рисков. Как правило, менеджер пытается составить инвестиционный портфель доходность, которого как можно ближе соответствовала бы доходности рыночного индекса. Такой подход называется «Индексная стратегия управления инвестиционным портфелем».
Слайд 28 Рыночный индекс включает в себя взвешенный набор различных акций.
Например, индекс ММВБ включает в себя 30 различных акций.
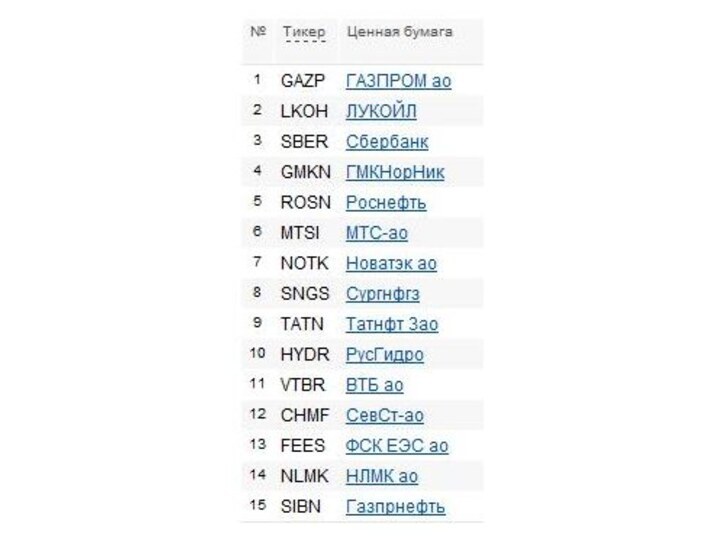
Также есть капитализационные индексы. Капитализация – показатель характеризующий масштабы операций на рынке и определяется как суммарная рыночная стоимость обращающихся ценных бумаг. Например, капитализационные индекс ММВБ MICEX LC, MICEX MC, MICEX SC с высокой, стандартной и базовой капитализацией.Итак, перед портфельным управляющим ставится задача: составить портфель из 4-х акций, что бы он как можно сильнее описывал рыночный индекс. Напомню, что в рыночный индекс входит намного больше акций, но любой инвестор всегда ограничен в средствах. Построим инвестиционный портфель из пяти акций, который бы наиболее полно соответствовал рыночному индексу. Для этого возьмем капитализационный индекс MICEX LC, состоящий из 15 акций. (Данные взяты с биржи ММВБ www.micex.ru)
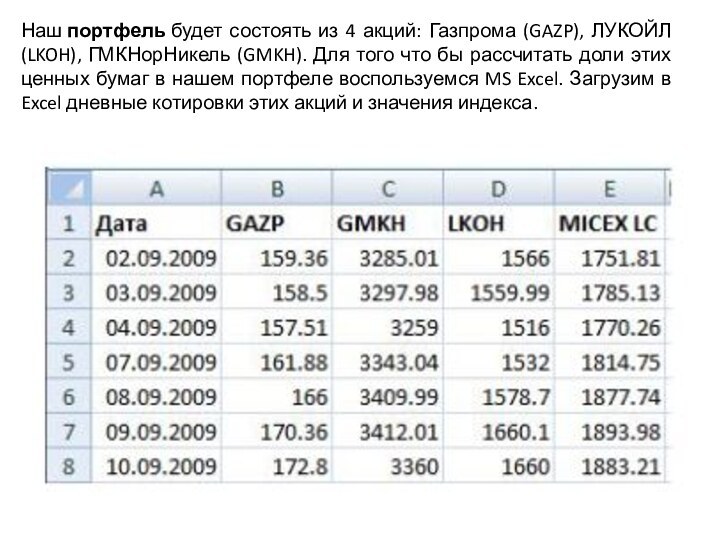
Слайд 30 Наш портфель будет состоять из 4 акций: Газпрома (GAZP), ЛУКОЙЛ
(LKOH), ГМКНорНикель (GMKH). Для того что бы рассчитать доли
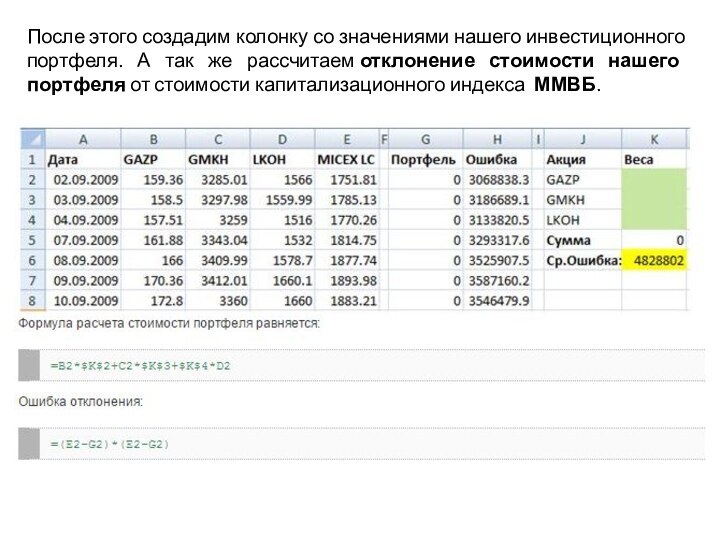
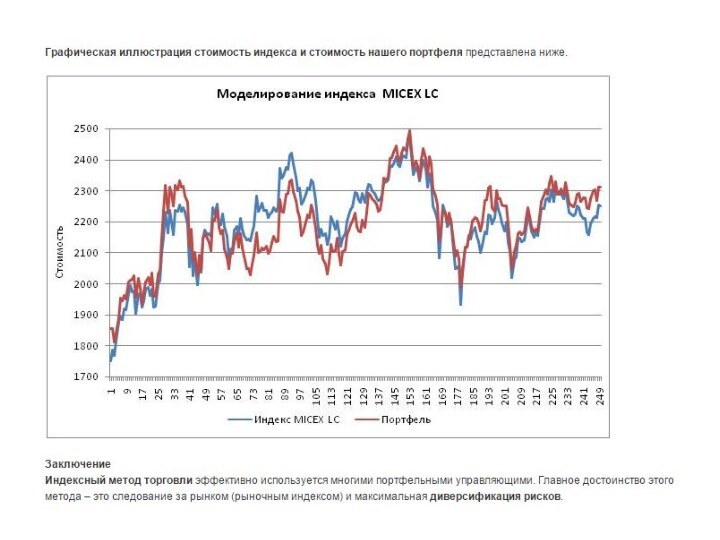
этих ценных бумаг в нашем портфеле воспользуемся MS Excel. Загрузим в Excel дневные котировки этих акций и значения индекса.Слайд 31 После этого создадим колонку со значениями нашего инвестиционного
портфеля. А так же рассчитаем отклонение стоимости нашего портфеля от стоимости
капитализационного индекса ММВБ.
Слайд 35
4. Модель квази-Шарпа
Формирование инвестиционного портфеля на основе Quasi-Sharpe
model
Для эффективной работы на нестабильных фондовых рынках была предложена новая модель формирования инвестиционного
портфеля, которая получила название модель Quasi-Sharpe. Эта модель основана на взаимосвязи доходности каждой ценной бумаги из всего множества N ценных бумаг с доходностью единичного портфеля их этих бумаг. В общих чертах модель «Квази- Шарпа» сильно походит на модель предложенную У. Шарпом, но есть некоторые отличия. Рассмотрим основные допущения модели «Квази- Шарпа»:1. Доходность ценной бумаги рассчитывается как математическое ожидание доходностей. Это допущение есть и в модели Шарпа.
2. Единичный портфель представляет собой портфель, состоящий из всех рассматриваемых ценных бумаг, взятых в одинаковой пропорции. В модели Шарпа за эталонный портфель (бенчмарк) берется так называемый рыночный портфель, динамику которого часто описывает фондовый индекс. Для российского фондового рынка это индекс РТС (RTSI), для украинского рынка индекс ПФТС, для американского фондового рынка это S&P500.
Слайд 36 3. Доходность ценной бумаги прямо пропорционально доходности единичного
портфеля. То же предположение в модели Шарпа для рыночного
портфеля.4. Риск ценной бумаги рассчитывается как чувствительность изменения доходности ценной бумаги от изменения доходности единичного портфеля. Аналогично для модели Шарпа.
5. В отличии от модели Шарпа, за безрисковую ставку берется средняя доходность единичного портфеля, а не государственные обязательства.
Слайд 37 Модель «Квази – Шарпа» соединяет доходность ценной бумаги с
доходностью единичного портфеля и риском этой ценной бумаги с
помощью функции линейной регрессии. Формула доходности ценной бумаги следующая:Ri- доходность ценной бумаги;
Rsp- доходность единичного портфеля;
βi- коэффициент чувствительности к изменению доходности ценной бумаги, коэффициент регрессии в уравнении доходности;
– средняя доходность ценной бумаги;
– средняя доходность единичного портфеля.
Слайд 38 Необходимо сказать несколько слов об измерении риска в
данной модели. Риск измеряется с помощью коэффициента бета (β), который характеризуется
степенью чувствительности к изменению доходности единичного портфеля. Чем выше коэффициент бета, тем сильнее изменяется доходность ценной бумаги от колебания доходности единичного портфеля.В модели «Квази-Шарпа » риск ценной бумаги представляет собой совокупность коэффициента бета и остаточного риска (σri). Остаточным риском называют степень разброса значений доходности ценной бумаги относительно линии регрессии.
Доходность в модели «Квази – Шарпа» рассчитывается как:
Слайд 39
Риск же рассчитывается по следующей формуле:
Задача формирования оптимального портфеля по
модели «Квази-Шарпа», где мы максимизируем доходность инвестиционного портфеля и
устанавливаем допустимый уровень риска, будет выглядеть следующим образом.Слайд 40 Обратная задача формирования оптимального портфеля, где мы минимизируем
общий риск инвестиционного портфеля с фиксированным уровнем доходности, имеет
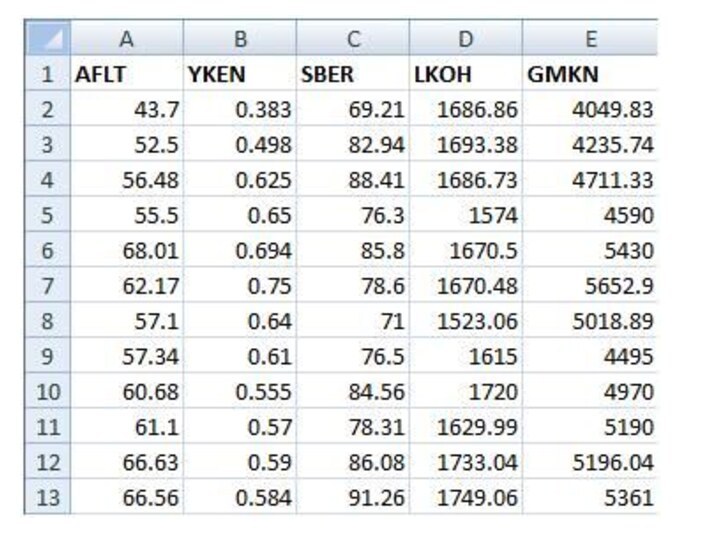
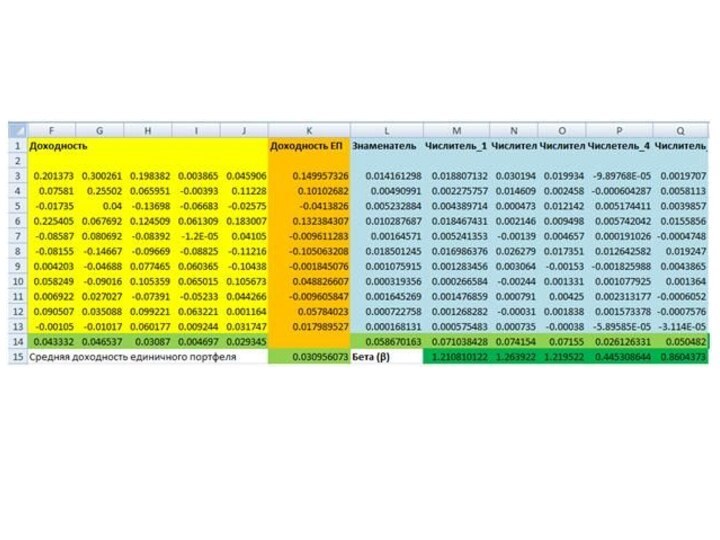
следующий вид:Давайте на конкретном примере рассмотрим применение модели «Квази – Шарпа» для российского фондового рынка. Данные по котировкам возьмем с сайта finam.ru (или сайта биржи). За последний год возьмем котировки таких крупных компаний, как Газпром (GAZP), Аэрофлот (AFLT), Якутэнерго (YKEN), Сбербанк (SBER), Лукойл (LKOH) и ГМК Норникель (GMKN). Мы сразу отбросим из рассмотрения акции Газпрома, так как за рассматриваемый год они показали отрицательную прибыль. Итак, занесем все данные в таблицу Excel. На рисунке ниже показаны месячные данные по стоимости акций этих компаний с 10.10.2009 по 10.10.2010.
Слайд 42
Следующим этапом рассчитаем доходности этих акций по следующей формуле:
Где:
Ri- текущая
доходность акции; Pi- текущая стоимость акции; Pi-1 – стоимость акции в предыдущем
периоде.Формула в Excel будет выглядеть следующим образом:
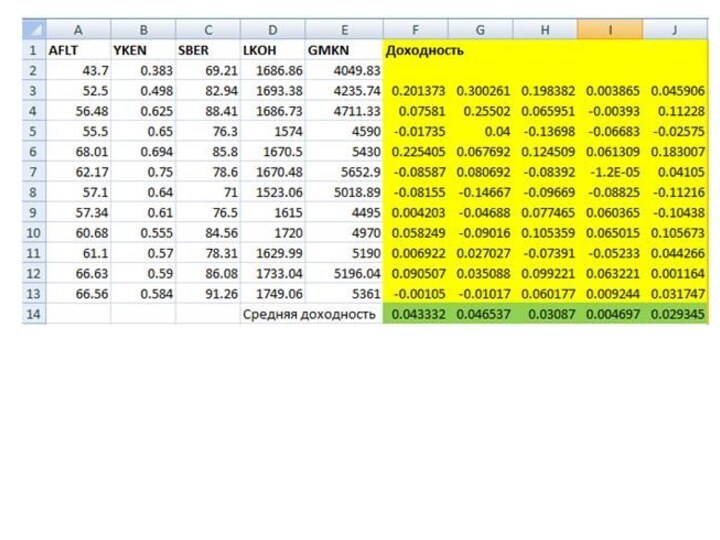
Слайд 43 И аналогично рассчитываем доходности всех акций. На рисунке ниже
показан расчет доходности по акциям. Каждый столбец представляет месячные
доходности каждой акции.Следующим этапом, для каждой акции рассчитаем среднее значение доходности за весь год, то есть за все временные отрезки. Формула для расчета следующая:
Rit- доходность i-ой акции за период t;
T- рассматриваемое количество временных периодов (в нашем случае 12).
Формула расчета в Excel средней доходности (AFLT) следующая:
Аналогично рассчитываются остальные доходности акций.
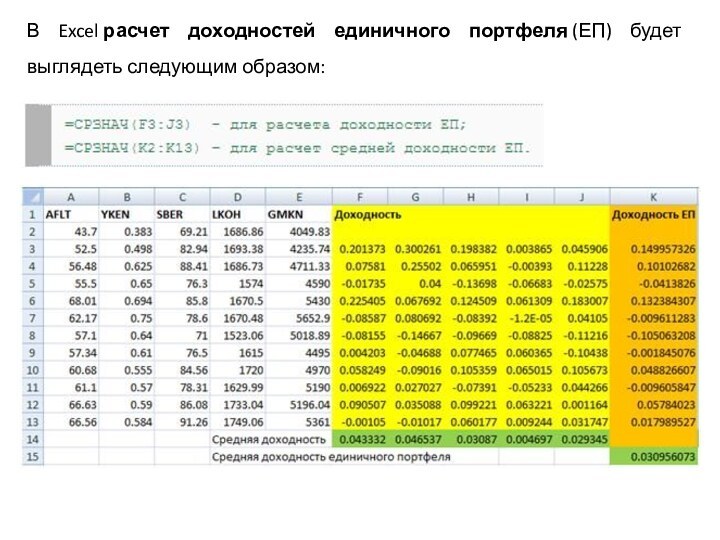
Слайд 45 Далее рассчитаем доходность единичного портфеля. Сделав необходимые расчеты, рассчитаем доходности
единичного портфеля и его среднюю доходность за все периоды.
Доходность единично портфеля представляет собой доходность портфеля составленного из используемых акций, взятых в равных пропорциях. Доходность единичного портфеля рассчитывается следующим образом:Где:
–доходность единичного портфеля;
– доходность i-ой ценной бумаги за период t.
Средняя доходность единичного портфеля за все периоды рассчитывается так:9
средняя доходность единичного портфеля;
Т – рассматриваемое количество временных периодов;
– доходность единичного портфеля.
Слайд 47 Далее рассчитаем чувствительность изменения доходности акции от изменения доходности единичного
портфеля. Чувствительность показывает коэффициент бета (β). И формула его
вычисления следующая:Для упрощения расчета посчитаем сначала знаменатель коэффициента бета, он для всех акций будет одинаков, а после числитель.
Столбец знаменателя (L) рассчитывается по формуле:
И в ячейке L14 происходит расчет непосредственно знаменателя по формуле:
Слайд 48 Для вычисления числителя по периодам коэффициента бета сначала
воспользуемся формулой.
Аналогично для других акций.
Суммируем полученные результаты за все
периоды, то есть непосредственно рассчитываем числителя. Расчеты находятся в ячейках L14-Q14 по формулам:Коэффициент бета (β) будет рассчитан как отношение числителей к знаменателю.
=(F3-F$14)*($K3-$K$15) для акций Аэрофлота, колонка М
Слайд 50 Следующим этапом рассчитаем остаточный риск, который представляет собой
степень разброса доходности ценной бумаги относительно линии регрессии. Формула расчета
остаточного риска следующая:Сначала рассчитываем остаточный риск на каждый период:
После рассчитываем остаточный риск за все периоды (R14-V14):
=СТЕПЕНЬ(F3-F$14-M3*M$15;2)
Слайд 51
При формировании инвестиционного портфеля из этих акций нам
еще потребуется рассчитать риск единичного портфеля:
Риск единичного портфеля равен (U15):
Слайд 52
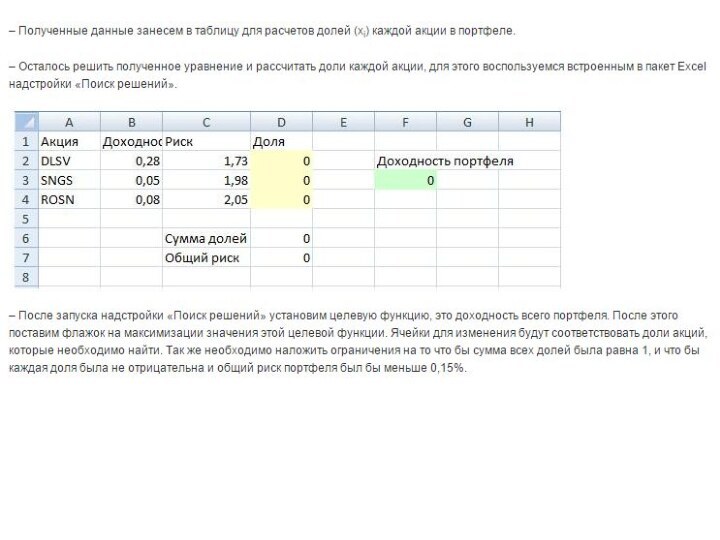
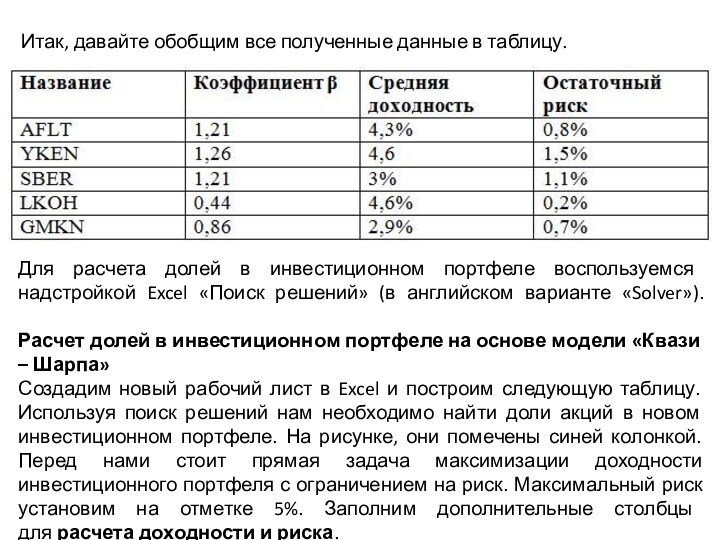
Итак, давайте обобщим все полученные данные в таблицу.
Для
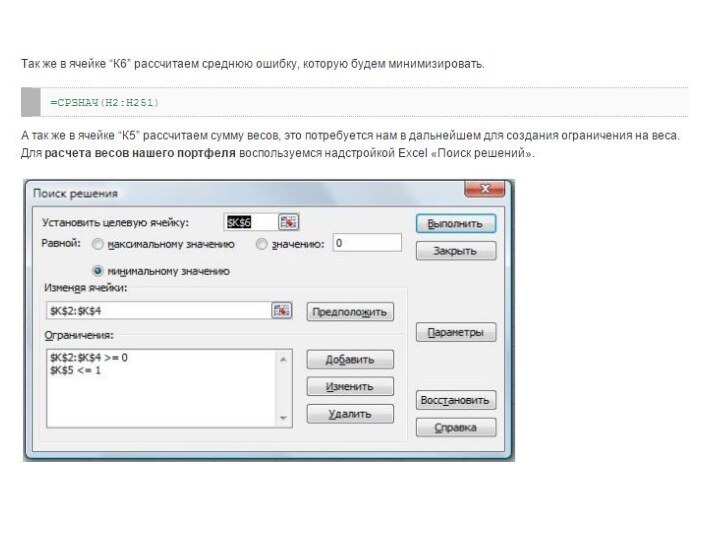
расчета долей в инвестиционном портфеле воспользуемся надстройкой Excel «Поиск
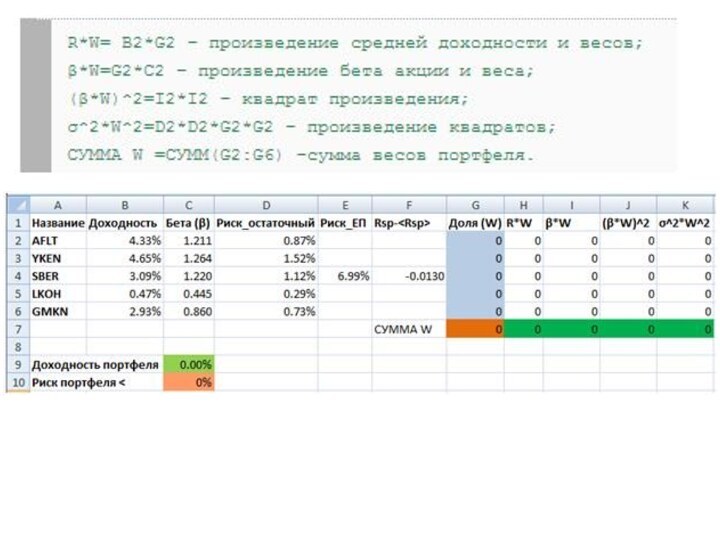
решений» (в английском варианте «Solver»). Расчет долей в инвестиционном портфеле на основе модели «Квази – Шарпа»Создадим новый рабочий лист в Excel и построим следующую таблицу. Используя поиск решений нам необходимо найти доли акций в новом инвестиционном портфеле. На рисунке, они помечены синей колонкой. Перед нами стоит прямая задача максимизации доходности инвестиционного портфеля с ограничением на риск. Максимальный риск установим на отметке 5%. Заполним дополнительные столбцы для расчета доходности и риска.
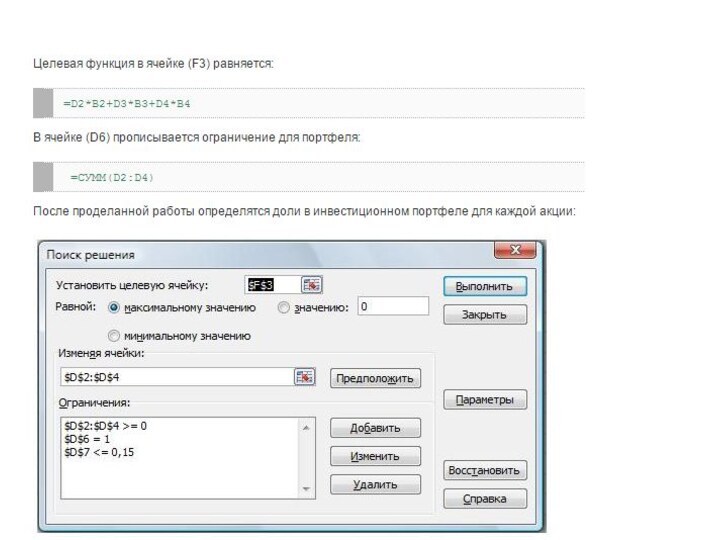
Слайд 54 Формула расчета целевой ячейки с доходностью портфеля (C9)
будет следующая.
=СУММПРОИЗВ(B2:B6;G2:G6)+F4*СУММПРОИЗВ(C2:C6;G2:G6)
Формула расчета риска инвестиционного портфеля:
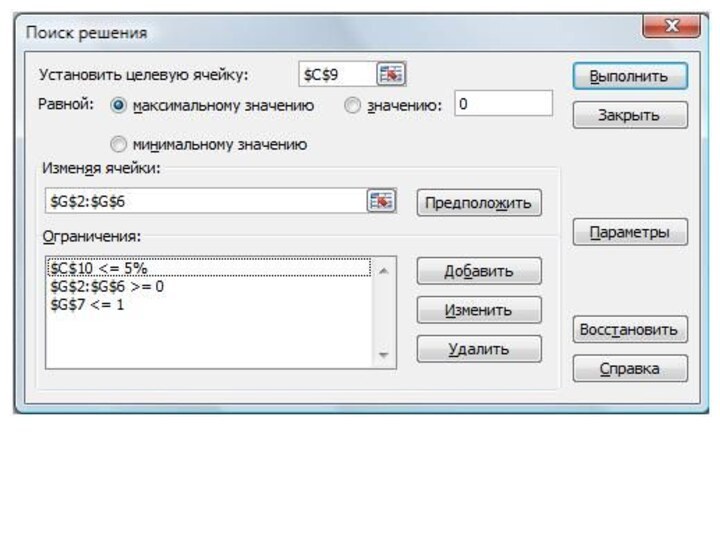
Для нахождения оптимальной структуры
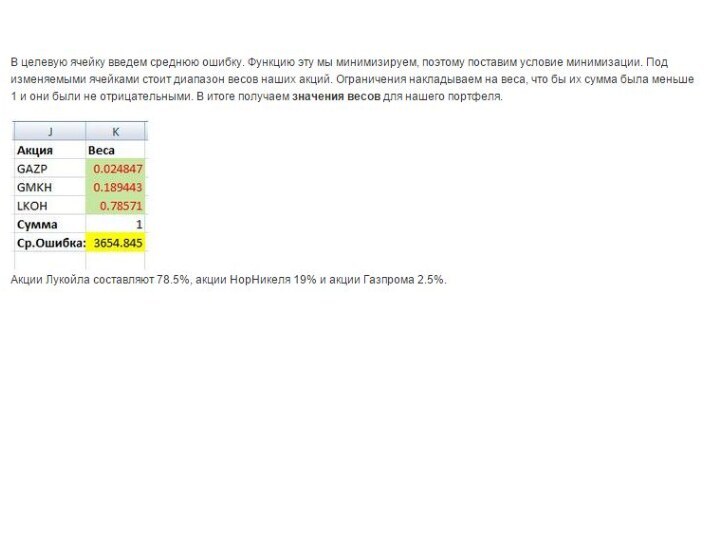
портфеля загрузим надстройку «Поиск решений». Выберем целевую функция – ячейку с доходностью (С9). Ее мы будем максимизировать. Для этого будем изменять доли акций в портфеле – диапазон ячеек C2:G6. Необходимо так же наложить ограничения на риск и веса акций. Веса должны быть положительны, сумма их должна не превышать единицы и риск рассчитанный в ячейке С10 должен быть меньше 5%.Слайд 56 В итоге мы получаем расчет долей акций в
нашем инвестиционном портфеле. В итоге мы получили следующее соотношений
весов акций в портфеле. Доля акций Аэрофлота (AFLT) составляет 37.7%, доля акций Якутэнерго (YKEN) составляет 40.5%, доля акций Сбербанка (SBER) 1.3%, доля акций Лукойла (LKOH) 0% и доля акций ГМКНорНикель (GMKN) 20.5%.