Слайд 2
Два класса городских моделей
Пять моделей города
Изолированное государство Тюнена
Концентрическая
модель Бёрджеса
Секторная модель Хойта
Многоядерная модель Ульмана-Харриса
Факторная экология
Пять моделей системы
городов
Модель центральных мест Кристаллера – Лёша
Правило Ципфа
Диффузия нововведений Хагерстранда
Гравитационные модели и теория поля потенциалов
Модель главных потенциалов
Слайд 3
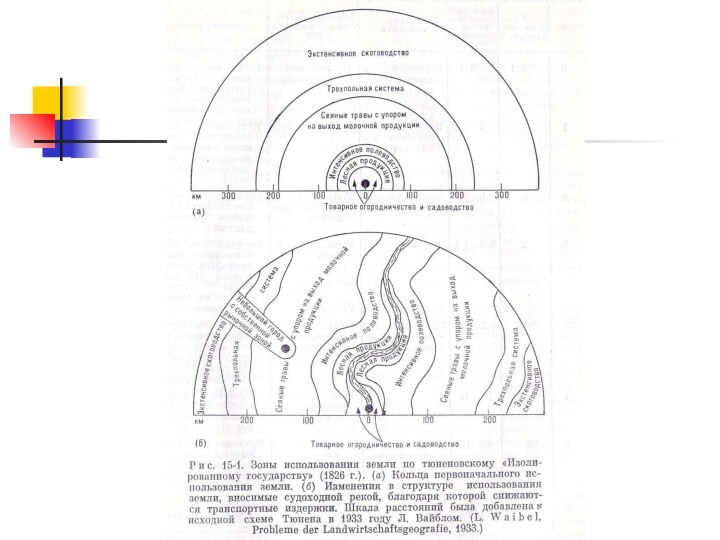
Модель фон Тюнена (1830-е годы)
Исходные допущения
Однородная равнина с
городом в центре
Равнина – сельское хозяйство, город – рынок
Одинаковое
плодородие + изотропность
Отсутствие эффекта масштаба (равный размер земельных участков)
Одинаковые издержки производства
Расстояние равнозначно объёму продукции
Слайд 4
Модель фон Тюнена
Расстояние до города
Прибыль
d
P
T1
T2
T3
d1
d2
d3
T4
Слайд 5
Модель фон Тюнена –
скрытое допущение
Товар с худшей
транспортабельностью должен стоить дороже
Если αb < αm, то
обязательно Pb > Pm
Правило Дана:
система цен устанавливается в городе таким образом, чтобы дать пространство каждому товару в тех пропорциях, которые нужны горожанам.
Слайд 6
Модель фон Тюнена - результаты
1 пояс. Овощеводство, интенсивное
молочное производство
2 пояс. Лесная промышленность
3 пояс. Зерноводство (интенсивные культуры)
4
пояс. Зерноводство (экстенсивные культуры)
5 пояс. Пастбищное животноводство
Слайд 8
Модель фон Тюнена - итоги
Первая модель цены земли
Родоначальник
класса моделей – «очаг воздействия»
Философское толкование (Б.Б.Родоман):
Переход количества в
качество
Структура, функция, местоположение
Давление места
Реальный мир – искажение идеальных моделей
Слайд 9
Критика модели фон Тюнена
Чрезмерная абстракция
Противоречит реальности (на самом
деле – Техас, Уттар-Прадеш, Саскачеван, Чикаго)
Карл Маркс: «"Мекленбургский юнкер
(впрочем с немецкой манерой мышления), который рассматривал свое имение Теллов как воплощение сельского хозяйства вообще, а Шверин в Мекленбурге как воплощение города вообще и, исходя из этих предпосылок, с помощью наблюдения, сопоставлений, практического счетоводства и т.п. самостоятельно конструирует для самого себя рикардовскую теорию земельной ренты. Это достойно уважения и в то же время смешно".
Слайд 10
Модели территориальной организации города
Концентрические кольца Берджесса (1925)
Расширение зон
по направлению к периферии
Секторная модель Хойта (1931)
Изучение распределения арендной
платы на жилье
Многоядерная модель Харриса-Ульмана (1946)
Факторная экология (70-е годы)
Семейный статус (кольца), доход (сектора), раса
Жизненный цикл семьи
Слайд 12
Модель Хойта
Ветер
Жилье среднего класса
Промышленная зона
Жилье низкого класса
Жилье высшего
класса
Слайд 13
Теория центральных мест (Вальтер Кристаллер, Август Лёш)
Кристаллер: 1933,
Южная Бавария
Классический немецкий путь: от исследования реальности к абстрактной
модели
Классические допущения:
Однородная равнина
Равномерная «шахматная» сеть поселений
Спектр производств с разным масштабом предприятий и экономией на масштабе
Слайд 15
Теория центральных мест:
постулаты
Компромисс экономии на масштабе и близости
к потребителю
Задача Хотеллинга «Мороженщики на пляже», 1929 год
Возникновение
центральных мест с зонами обслуживания
Три вида услуг:
повседневные (везде),
периодические (часто)
эпизодические
Центральные места различаются по размерам из-за разного набора размещённых в них услуг
Центральные места образуют зоны обслуживания
Зоны – шестиугольники (оптимальный способ замощения)
Слайд 16
Теория центральных мест: варианты оптимизации
Оптимизация рыночной структуры (К=3)
Оптимизация
транспортной структуры (К=4)
Оптимизация административной структуры (К=7)
Слайд 18
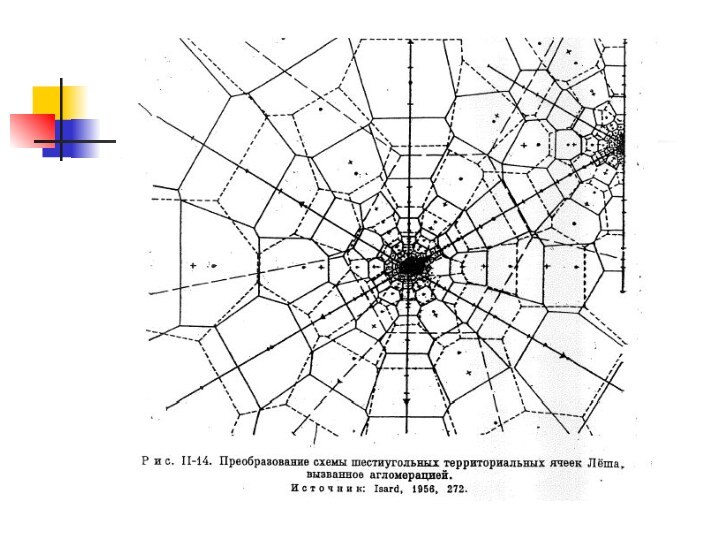
Искажения правильной решетки
Искажения, обусловленные агломерацией (модификация У.Изарда)
Искажения, обусловленные
локализацией ресурсов
Искажения, обусловленные, магистральными путями сообщения
Слайд 20
Экономический ландшафт: модификация модели В.Кристаллера А.Лёшем
Максимальное совмещение функций
центральных мест
Построение иерархии «сверху – вниз»
«Богатые» и «бедные» городами
секторы
Связь концентрических и секторных моделей
Слайд 22
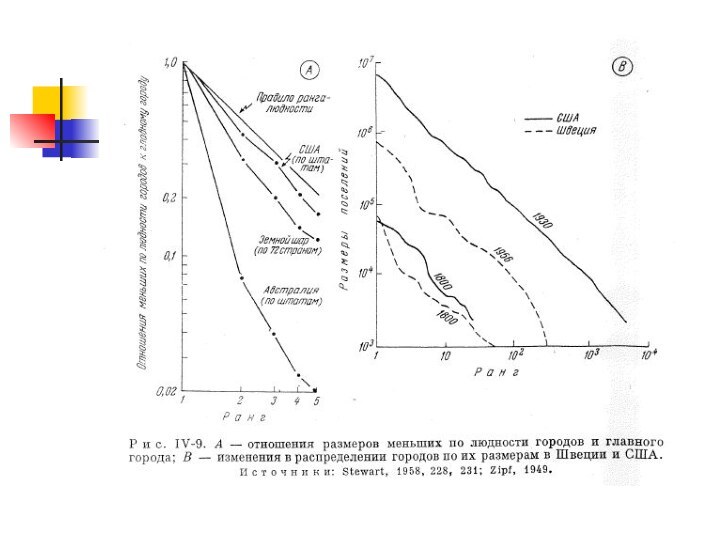
Правило «ранг-размер» (Правило Ципфа)
Pn = P1/n
Pn – население
города n-го ранга
P1 – население крупнейшего города страны
Слайд 23
Правило Ципфа
Эмпирическое правило
Возможные направления использования
Оценка деформации городских систем
(мегацефалия, двуголовость, субсистемы)
Оценка потенциала роста/риска упадка отдельных городов
Использование при
разработке региональной политики
Слайд 25
Правило Ципфа для российских городов: реальность 2000 в
сопоставлении с идеальным распределением
200
250
300
350
400
450
1
7
13
19
25
31
37
43
49
55
61
67
73
79
85
91
97
103
109
115
121
127
133
139
145
151
157
163
Ранг
Размер
Слайд 26
Трудности с правилом Ципфа:
Сильная зависимость от способов подсчёта
людности городов (административные границы, урбанизированный ареал, агломерация)
Хорошо работает только
с 25-35 первыми городами
Слайд 27
Диффузия нововведений Т.Хагерстранда
Тезис: процесс не охватывает всю территорию
сразу, а возникает сначала в неких точках и распространяется
отсюда по неким законам, упорядоченно.
Двойная упорядоченность:
по расстоянию от очага
по иерархии
Слайд 28
Диффузия нововведений: стадии процесса
Первоначальная - в главном центре
Диффузия
- охват новых центров
Конденсация - одинаковая скорость повсюду
Насыщение -
медленный подъем во всех незаполненных местах.
ПРИМЕРЫ: холера, картофель, трамвай, радио, телевидение, субурбанизация
Слайд 29
Диффузия нововведений:
динамика по расстояниям (поясам)
и ступеням иерархии
Слайд 30
Гравитационные модели
Интенсивность взаимодействия между городами
Псевдоаналогия с законом Ньютона-Кулона
На
деле – запись пропорциональности
Показатель степени отражает трение пространства
зависит от
средств сообщения: чем лучше, тем меньше экспонента
В Африке она выше, чем в Дании, а в 1880 г. выше, чем в 2000
Слайд 31
Географическая теория поля
или модель потенциалов
Кларка-Медведкова
Потенциал точки
равен сумме отношений людности каждого города к расстоянию от
него до данной точки
Vn=ε(Pm/Lªnm) где Р – людность города,
L – расстояние, ª - экспонента
Затруднения в истолковании:
В чём содержательный смысл меры – чел./км?
Как учесть население в самой точке, где L=0 ?
Что обозначает рельеф поля потенциалов?
L
Слайд 32
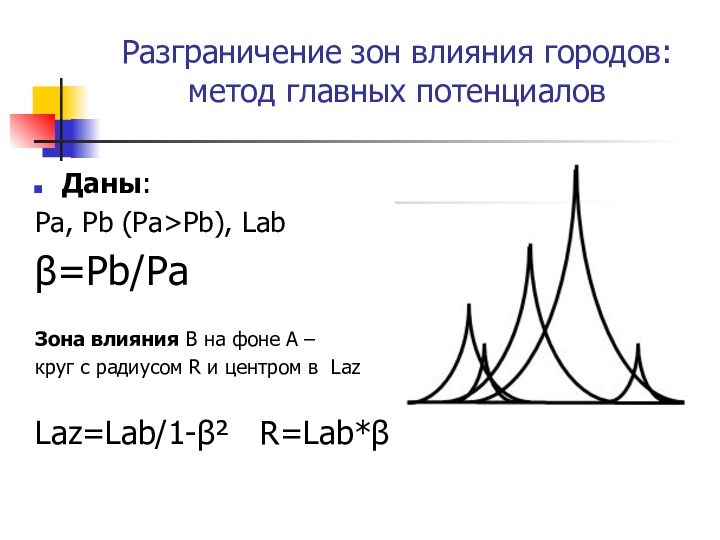
Разграничение зон влияния городов:
метод главных потенциалов
Даны:
Pa, Pb
(Pa>Pb), Lab
β=Pb/Pa
Зона влияния В на фоне А –
круг с
радиусом R и центром в Laz
Laz=Lab/1-β² R=Lab*β
Слайд 33
Разграничение зон влияния городов:
трехмерное изображение
Слайд 34
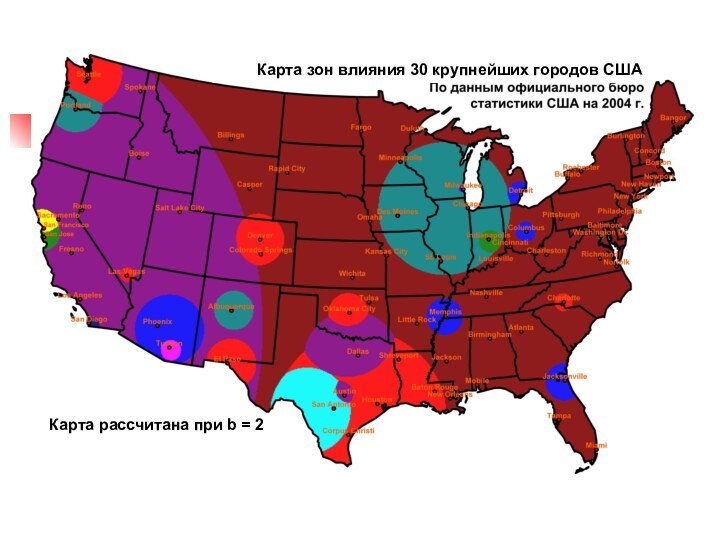
Карта рассчитана при b = 2
Карта зон влияния
30 крупнейших городов США
Слайд 35
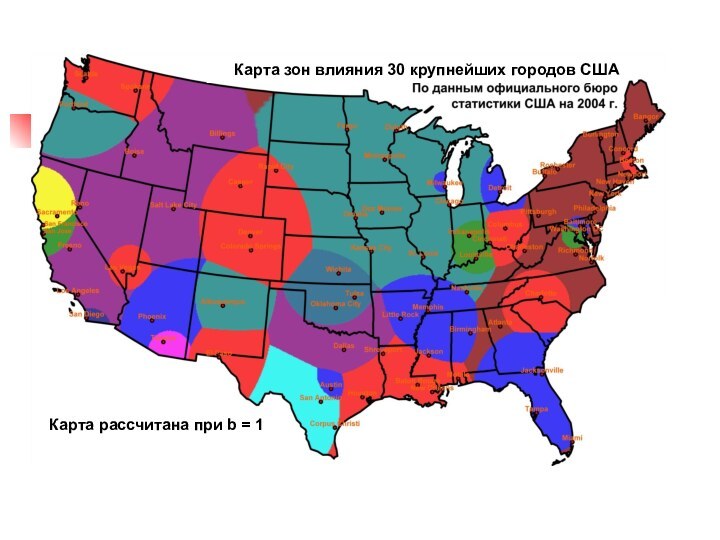
Карта зон влияния 30 крупнейших городов США
Карта рассчитана
при b = 1
Слайд 36
Карта рассчитана при b = 2
Карта рельефа потенциалов
30 крупнейших
городов США
Главный потенциал местности (у.е.)
Слайд 37
Карта рассчитана при b = 1
Карта рельефа потенциалов
30 крупнейших
городов США
Главный потенциал местности (у.е.)