Слайд 2
6.1. Анализ переменных потоков платежей
Слайд 3
Нерегулярный поток платежей
Временные интервалы между последовательными платежами в
нерегулярном потоке могут быть любыми, не постоянными, любыми могут
быть так же и члены потока.
Обобщающие характеристики в этом случае получают только путем прямого счета:
Слайд 4
где t - время от начала потока платежей
до момента выплаты,
Rt – сумма платежа.
Пример 5.1. Четыркин
Слайд 5
Переменная рента с разовыми изменениями размеров платежа
Пусть общая
продолжительность ренты n и этот срок разбит на k
участков продолжительностью n1, n2, … , nk, в каждом из которых член ренты постоянен и равен Rt (t = 1, 2, …, k), но изменяется от участка к участку.
Слайд 6
Тогда наращенная сумма для годовой ренты постнумерандо (p
= 1, m = 1)
а современная величина
Слайд 7
Рента с постоянным абсолютным приростом платежей
Пусть размер платежей
изменяется с постоянным приростом a (положительным или отрицательным). Если
рента годовая постнумерандо, то размеры последовательных платежей составят R, R + a, R + 2a,…, R + (n - 1)a.
Величина t-го члена равна
Rt = R + (t - 1)a.
Слайд 8
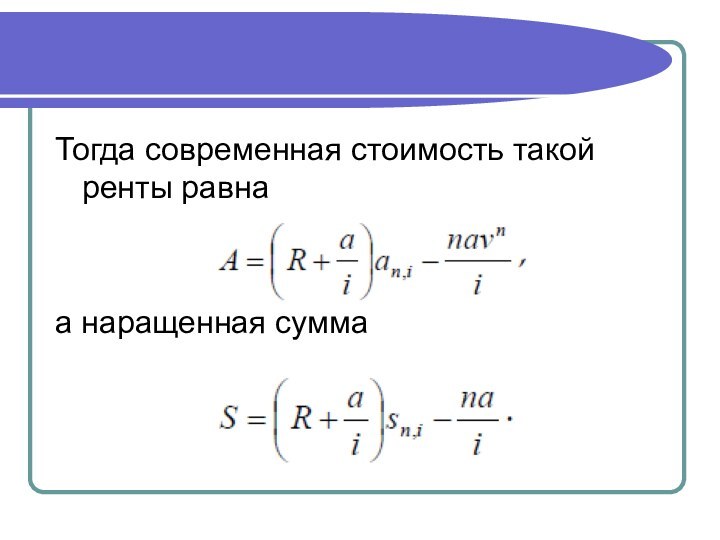
Тогда современная стоимость такой ренты равна
а наращенная сумма
Слайд 10
Современная величина
а наращенная сумма
Слайд 11
6.2. Ренты с постоянным относительным изменением платежей
Если платежи
годовой ренты изменяются с постоянным темпом роста q, то
члены ренты будут представлять собой ряд:
R, Rq, Rq2,…, Rqn-1.
Слайд 12
Для того чтобы получить современную величину, дисконтируем эти
величины:
Rv, Rqv2, …, Rqn-1vn
получили геометрическую прогрессию.
Слайд 14
Наращенная сумма ренты
S = А (1+i )n =
Слайд 16
6.3. Постоянная непрерывная рента
Во всех рассмотренных выше рентах
предполагалось, что члены потока платежей поступают дискретно - через
фиксированные интервалы времени (периоды ренты).
Вместе с тем иногда более адекватное описание потока платежей достигается, когда он воспринимается как непрерывный процесс.
Слайд 17
Рассмотрим постоянную непрерывную ренту, к которой применяется годовая
дискретная процентная ставка.
По определению у непрерывной ренты
Слайд 18
Найдем коэффициент приведения такой ренты
Для этого
необходимо найти предел коэффициента при ведения р-срочной ренты при
Слайд 19
Непосредственная подстановка р в знаменатель приводит к неопределенности:
Слайд 20
Раскроем неопределенность, применив правило Лопиталя.
Слайд 22
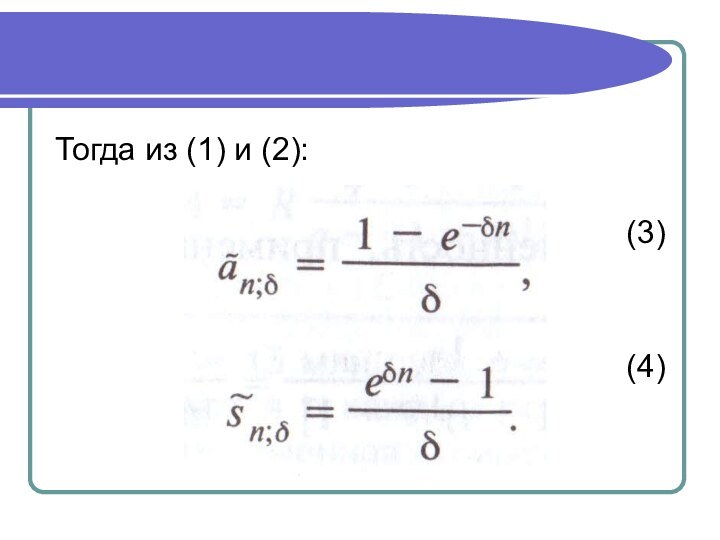
Аналогичным путем получим коэффициент наращения непрерывной ренты:
(2)
Слайд 23
Переход от дискретных платежей постнумерандо к непрерывным увеличивает
коэффициенты приведения и наращения в i / ln(1+i) раз
Слайд 25
ПРИМЕР (*)
Ожидается, что доходы от эксплуатации месторождения полезных
ископаемых составят 1 млрд руб. в год, продолжительность разработки
10 лет, отгрузка и реализация продукции непрерывны и равномерны. Найти капитализированную стоимость дохода при дисконтировании по ставке 10.
Слайд 27
Формулы предполагают непрерывное поступление платежей и дискретное начисление
процентов.
Более "естественным" является положение, когда оба процесса (поступление
денег и наращение процентов) непрерывны.
i = еδ - 1
Для
получения формул соответствующих коэффициентов воспользуемся формулами эквивалентности между непрерывными и дискретными ставками
δ= ln(l + i); i = еδ - 1
Слайд 30
Примечание:
Формулы (1) – (4) дают одинаковые результаты только
в том случае, когда непрерывные и дискретные ставки являются
эквивалентными.
Слайд 31
Пример
Пусть в примере * дисконтирование осуществляется по
силе роста 10, тогда
Слайд 33
Определение срока для постоянных непрерывных рент
Слайд 34
Аналогично для случая, когда исходной является наращенная сумма
ренты:
Слайд 35
6.4. Конверсия аннуитетов
В практике иногда возникает необходимость
изменить условия финансового соглашения, предусматривающего выплату аннуитетов, т.е. конвертировать
ренту.
Слайд 36
1) Выкуп ренты
Выкуп ренты представляет собой замену предстоящей
последовательности выплат единовременным платежом.
Из принципа финансовой эквивалентности (ФЭ)
следует, что в этом случае вместо ренты выплачивается ее современная величина.
Слайд 37
2) Рассрочка платежей -
это замена единовременного платежа аннуитетом.
Для соблюдения принципа ФЭ современную величину ренты следует приравнять
величине заменяемого платежа. Определить член ренты или ее срок при остальных заданных параметрах.
Слайд 38
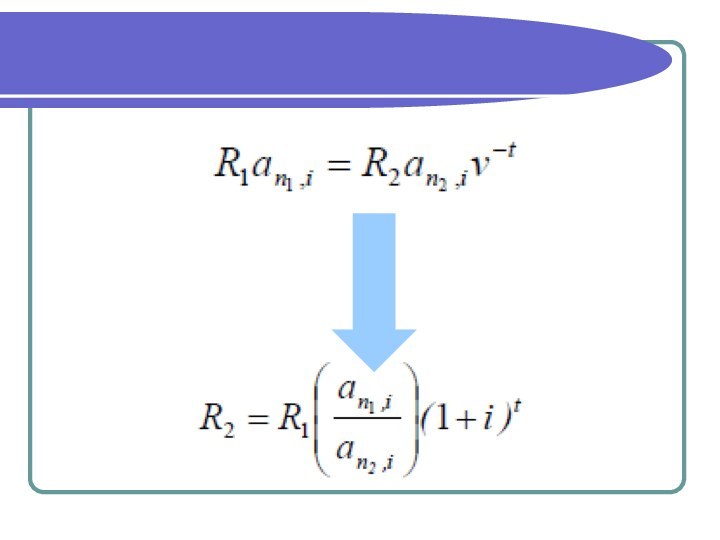
3) Замена немедленной ренты на отсроченную
Пусть имеется годовая
немедленная рента с параметрами R1, n1, i и ее
необходимо заменить на отсроченную на t лет ренту, т.е. начало ренты сдвигается на t лет.
Обозначим параметры отложенной ренты как R2, n2, i. Ставку процентов при этом будем считать неизменной.
Слайд 39
Типы расчетных задач:
А) Задан срок n2, требуется определить
размер R2.
Исходим из принципа ФЭ результатов, т.е. из равенства
современных стоимостей заменяемого и заменяющего потоков: A1=A2.
Слайд 42
Типы расчетных задач:
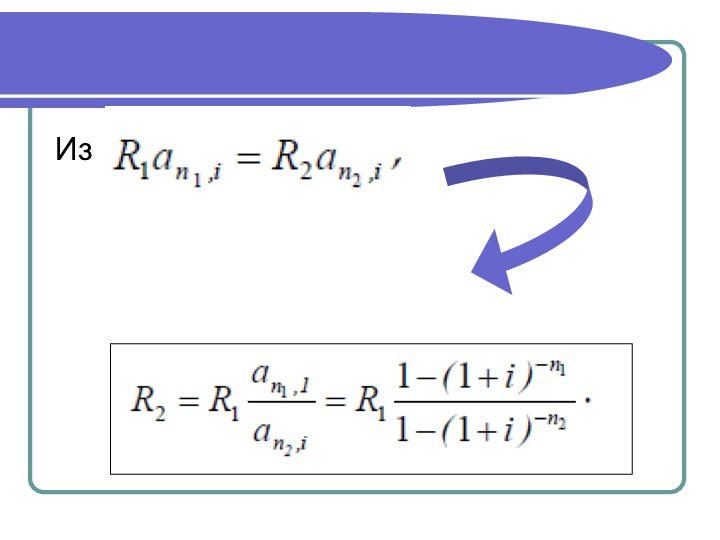
Б) Размеры платежей заданы, требуется определить
срок n2.
Пусть платежи годовой ренты одинаковыми: R2=R1=R. Исходя из
равенства современных стоимостей,
Слайд 43
+
последовательно приходим к выражению
+
Слайд 44
4) Изменение продолжительности ренты
Пусть имеется годовая обычная рента,
и у партнеров есть договоренность об изменении срока ренты,
т.е. вместо срока n1, принят новый срок n2. Тогда для эквивалентости финансовых результатов требуется изменение и размера платежа.
Слайд 46
5) Общий случай изменения параметров ренты
В случае одновременного
изменения нескольких параметров ренты, исходим из равенства A1=A2.
Если
годовая рента, то приводится к виду
Слайд 47
где
A1 подсчитывается заранее,
t – период (возможной)
отсрочки,
ряд параметров задается по согласованию сторон,
один параметр находится
из этого уравнения.
Слайд 48
6) Объединение рент
В случае объединения (консолидации) нескольких рент
в одну из принципа ФЭ обязательств до и после
операции следует, что
где A- современная величина заменяющей ренты,
Ak – современная величина k-ой объединяемой ренты.
Слайд 49
Объединяемые ренты могут быть любыми. Если заменяющая рента
постнумерандо является немедленной и задан срок n, то