- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Прогнозирование сезонных процессов
Содержание
- 2. ВведениеПрироде многих экономических явлений внутренне присуща повторяющаяся
- 3. Сезонные колебания- такие изменения уровня динамического ряда,
- 4. Прогнозирование с учетом сезонного фактора крайне важно
- 5. Общий вид индекса сезонностиОтношение исходных (эмпирических) уровней
- 6. В процессе прогнозирования сезонных изменений каждый уровень
- 7. Методы построения прогноза динамики с учетом сезонных
- 8. Прогноз базируется на двух компонентах:∙ Компонента тренда представляет
- 9. Сезонная компонента St имеет период Т0, т.е.
- 10. Построение прогнозной модели с аддитивной компонентой имеет
- 11. Методы построения прогноза динамики с учетом сезонных
- 12. Построение модели с мультипликативной компонентой. Первый способПостроение
- 13. Построение модели с мультипликативной компонентой. Второй способОпределение
- 14. Построение модели с мультипликативной компонентой. Второй способРасчет
- 15. Построение модели с мультипликативной компонентой. Второй способРасчет
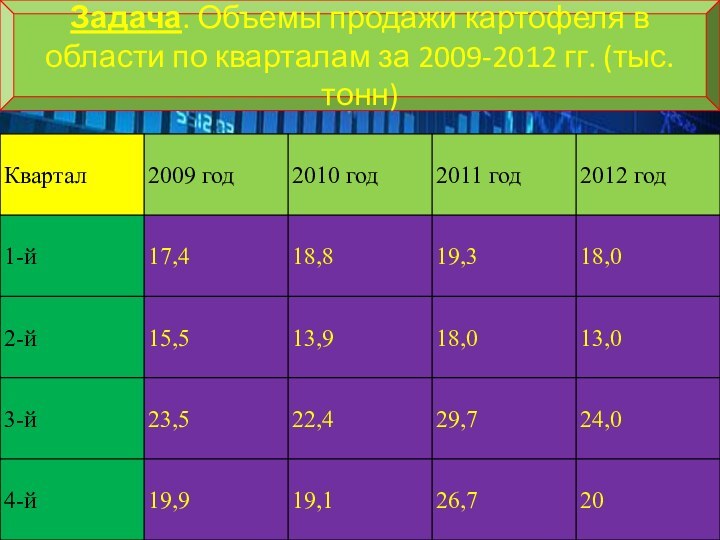
- 16. Задача. Объемы продажи картофеля в области по кварталам за 2009-2012 гг. (тыс. тонн)
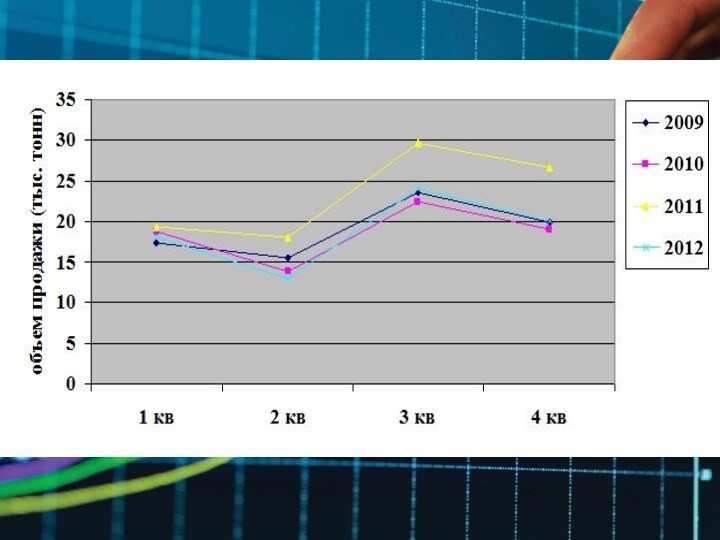
- 17. Требования задачи1. Постройте график исходных данных и
- 20. Ур = a * X + b,
- 21. Средняя относительная ошибкаε = 303,46/16 = 18,97% - точность прогноза является хорошей, поскольку входит в пределы 10-20%.
- 22. Вывод по темеПри решении практических задач для
- 23. Скачать презентацию
- 24. Похожие презентации




















Слайд 2
Введение
Природе многих экономических явлений внутренне присуща повторяющаяся во
времени неравномерность развития
причинамиСлайд 3 Сезонные колебания- такие изменения уровня динамического ряда, которые
вызываются влияниями
времени года.
Под сезонностью принято понимать устойчивую, повторяющуюся во
времени периодичность в развитии экономических явлений.В широком смысле слова термин «сезон» применим в прогнозировании к любым систематическим колебаниям.
Исследовать влияние сезонности можно по временным рядам, содержащим информацию о значениях показателя по кварталам, месяцам, неделям, дням, времени суток или часам.
Слайд 4 Прогнозирование с учетом сезонного фактора крайне важно для
принятия управленческих решений, примерами которых могут служить:
оценка достаточности
мощностей и потребности в резервных мощностях;выбор тактических приемов ценообразования, учитывающих неравномерность спроса;
оценка потребности в рабочей силе в периоды пиковых нагрузок и т.д.
Слайд 5
Общий вид индекса сезонности
Отношение исходных (эмпирических)
уровней ряда динамики yi,
к теоретическим (расчетным) уровням yti, выступающим в
качестве базы сравнения
Isi =
yi : yti Слайд 6 В процессе прогнозирования сезонных изменений каждый уровень временного
ряда можно представить как результат взаимодействия:
трендовой,
сезонной,
случайной компонент.
Тренд представляет
собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени.Сезонная составляющая - это периодически повторяющаяся компонента
Существует несколько способов оценки (типов моделей) их взаимодействия:
с аддитивной компонентой;
мультипликативной компонентой.
Слайд 7
Методы построения прогноза динамики с учетом сезонных колебаний
Модель
с аддитивной компонентой. Уравнение временного ряда с учетом сезонных
колебаний может быть представлено следующим образом:Yt = Тt + St + Et
где Тt – тренд динамического ряда – регулярная компонента, характеризующая общую тенденцию
St – сезонная компонента
Et – случайная компонента, образующаяся под влиянием различных причин
* Модель с аддитивной компонентой целесообразно использовать, если среднегодовые значения показателя остаются неизменными на протяжении длительного периода.
Слайд 8
Прогноз базируется на двух компонентах:
∙ Компонента тренда представляет тенденцию
временного ряда (базовой линии) к повышению либо к понижению.
∙ Компонента
сезонности представляет любое резкое повышение, понижение или пик базовой линии, которые происходят с одинаковым промежутком времени.
Слайд 9
Сезонная компонента St имеет период Т0, т.е.
St+То = St
Т0 = 12 для месячных данных
и Т0 = 4 для квартальных данных.
Величина Т0 содержится в Т целое число (m) раз, т.е.
Т = m Т0
Слайд 10 Построение прогнозной модели с аддитивной компонентой имеет несколько
этапов:
Построение и визуальный анализ графика сезонной волны.
Расчет значений
сезонной компоненты. Сезонная компонента должна показать, на сколько единиц в среднем фактические значения в тот или иной сезон отличались от усредненных за период. Для выделения сезонной компоненты может быть использован метод скользящей средней.Десезонализация данных (вычитание сезонной компоненты из фактических значений).
Расчет тренда на основе полученных десезонализированных данных (используя метод прогнозной экстраполяции).
Оценка ошибки для оценки степени соответствия модели исходным данным. Расчет среднеквадратического отклонения.
Построение прогноза с учетом сезонных колебаний.
Слайд 11
Методы построения прогноза динамики с учетом сезонных колебаний
2.
Модель с мультипликативной компонентой
Yt = Тt *St * Et
где Тt – тренд динамического
ряда – регулярная компонента, характеризующая общую тенденциюSt – сезонная компонента
Et – случайная компонента, образующаяся под влиянием различных причин
Слайд 12
Построение модели с мультипликативной компонентой. Первый способ
Построение и
визуальный анализ графика сезонной волны.
Расчет значений индекса сезонности.
Например, для расчета поквартальных индексов сезонности среднеквартальные значения показателей можно определить делением суммарных показателей за год на количество сезонов (четыре квартала); затем найти фактические индексы сезонности как отношение фактических значений к среднеквартальным. Индексы сезонности определить как среднее арифметическое из фактических индексов сезонности за соответствующий сезон.
Десезонализация данных, т.е. деление фактических значений на индекс сезонности.
Расчет параметров тренда для полученных десезонализированных данных.
Расчет трендовых значений, по полученному уравнению тренда.
Расчет прогнозных значений путем умножения трендовой составляющей и скорректированного индекса сезонности.
Оценка ошибки для оценки степени соответствия модели исходным данным; расчет среднеквадратического отклонения.
Построение прогноза с учетом сезонных колебаний.
Слайд 13
Построение модели с мультипликативной компонентой. Второй способ
Определение вида
тренда по фактическим значениям и расчет параметров тренда без
учета сезонных колебаний.Построение и визуальный анализ графика сезонной волны.
Расчет индексов сезонности. Формула индекса сезонности, определенного по средней арифметической, будет иметь следующий вид:
где yj — фактическое значение в момент времени j;
ȳ j — трендовое значение в момент времени j;
L — номер сезона;
k — количество сезонов (слагаемых) в рассматриваемом временном интервале.
Слайд 14
Построение модели с мультипликативной компонентой. Второй способ
Расчет скорректированных
индексов сезонности. Индексы сезонности, рассчитанные по формуле среднего арифметического,
необходимо скорректировать на коэффициент, учитывающий фактическую погрешность расчетов. Индекс корректировки можно определить по формуле:Скорректированные индексы сезонности рассчитать по формуле:
Слайд 15
Построение модели с мультипликативной компонентой. Второй способ
Расчет прогнозных
значений путем умножения трендовой составляющей и скорректированного индекса сезонности.
Оценка
ошибки для оценки степени соответствия модели исходным данным; расчет среднеквадратического отклонения.Построение прогноза с учетом сезонных колебаний.
Слайд 17
Требования задачи
1. Постройте график исходных данных и определите
наличие сезонных колебаний.
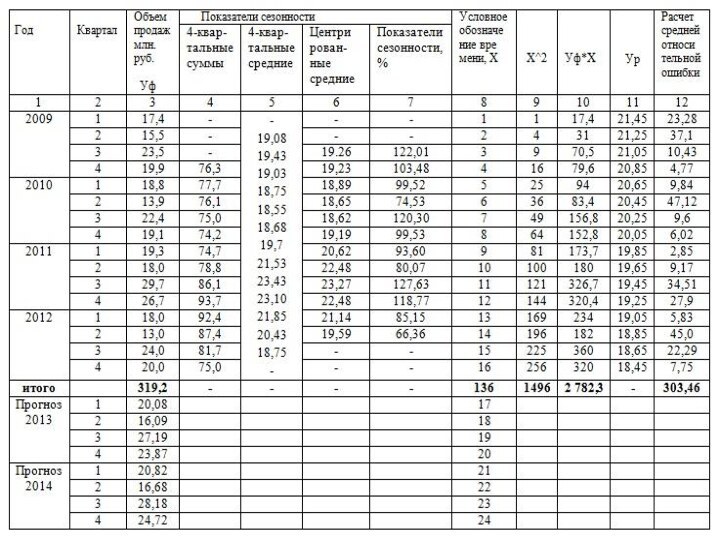
2. Постройте прогноз объема продажи картофеля в
области на 2013–2014 гг. с разбивкой по кварталам.3. Рассчитайте ошибки прогноза.
Слайд 20 Ур = a * X + b, (уравнение
тренда)
расчёт коэффициентов a и b
Уф – фактические значения
ряда динамики; n – число уровней временного ряда. а = [2 782,3 – (136*319,2)/16] / [1 496 – 1362/16] = 0,2
b = 319,2/16 – 0,2*136/16 = 18,25
Слайд 21
Средняя относительная ошибка
ε = 303,46/16 = 18,97% - точность
прогноза является хорошей, поскольку входит в пределы 10-20%.
Слайд 22
Вывод по теме
При решении практических задач для выбора
модели, наиболее адекватно отражающей закономерности рассматриваемого процесса, необходимо сравнить
показатели среднеквадратического отклонения.Та модель, где получена наименьшая ошибка, может быть признана наиболее точной для решения той или иной прогнозной задачи.