- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логика. Понятие, как форма мышления
Содержание
- 2. Понятие как форма мышления. Содержание и объем понятия.Виды понятий. Отношения между понятиями.
- 3. Понятие – это логическая мысль
- 4. Признак предмета – это то, в
- 5. Существенные признаки- это необходимо принадлежащие предмету признаки, выражающие его внутреннюю природу, его сущность
- 6. Несущественные признаки – могут принадлежать или не принадлежать предмету и которые не выражают его сущности
- 7. Предмет- это конкретные вещи, явления процессы,
- 8. Понятия образуются на основе представлений образов предметов
- 9. Материальным носителем понятия выступает слово или
- 10. Слова, закрепленные за понятиями (имена понятий)
- 11. К числу основных способов образования понятий относят: АнализСинтезСравнениеАбстрагированиеОбобщение
- 12. Анализ –мысленное расчленение предметов на их составные части, мысленное выделение в них признаков
- 13. Синтез – мысленное соединение в
- 14. Сравнение –мысленное установление сходства или различия предметов по существенным и несущественным признакам
- 15. Абстрагирование –мысленное выделение одних признаков предмета и временное отвлечение от других
- 16. Обобщение – мысленное объединение отдельных предметов в некотором понятии
- 17. Анализ, синтез, сравнение, абстрагирование, обобщение –
- 18. Логическая структура понятия Важнейшими логическими характеристиками всякого понятия являются его содержание и объем
- 19. Содержание понятия – это совокупность
- 20. Так в содержании понятия "логика" - наука
- 21. Объем понятия – это совокупность предметов, которая мыслится в данном понятии
- 22. Так объемом понятия "дом" являются все дома,
- 23. Виды понятий: а) по количественному признаку (по
- 24. по количественному признаку (по объему)единичныеобщие,регистрирующие (нулевые исчислимые), нерегистрирующие (неисчислимые )
- 25. Единичными понятиями являются те, которые отражают
- 26. Общими понятиями являются те, в которых
- 27. Пустые (нулевые) понятия — это
- 28. Регистрирующие (исчислимые) понятия —отражают поддающуюся исчислению область
- 29. Нерегистрирующие (неисчислимые) — все те понятия, объемы
- 30. по качественному признаку (по содержанию) утвердительные,
- 31. Утвердительными (положительными) понятиями являются те, которые отражают
- 32. Отрицательные понятия указывают на отсутствие любого признака,
- 33. Собирательные понятия специфичны, специфичны потому, что содержанием
- 34. Разделительные понятия — понятия, содержанием своим относимые
- 35. Конкретными понятиями являются те, которые отражают предмет
- 36. Абстрактными в логике считаются те понятия, которые
- 37. Соотносительными понятиями в логике считаются те, которые
- 38. Безотносительными понятиями являются все те, которые мыслятся
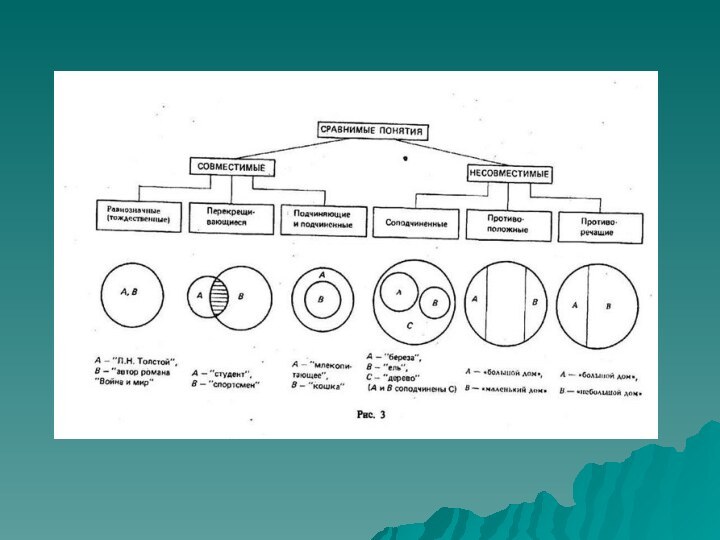
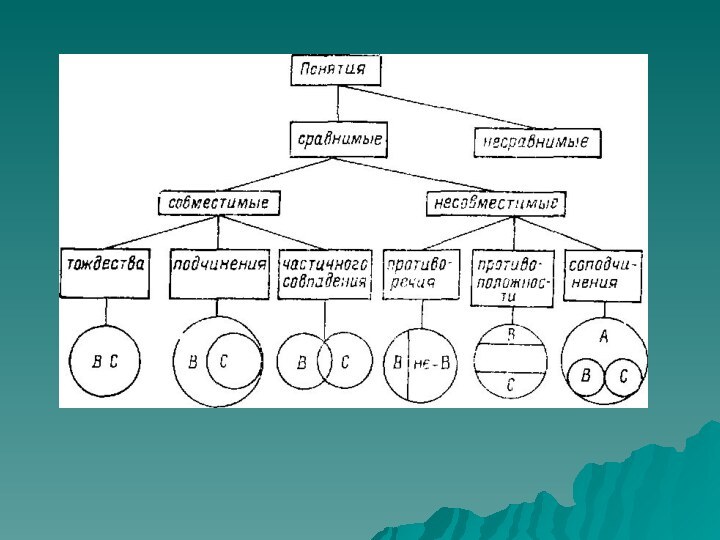
- 39. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ Виды понятий находятся
- 40. В отношении сравнимости находятся те понятия, в
- 41. Круги, с помощью которых изображаются логические классы, называются кругами Эйлера.
- 43. Диаграмма Эйлера- Венна Х – лев, ¬Х- не львы (дополнение к множеству Х)Х¬Х
- 44. В отношении несравнимости находятся те понятия, ни
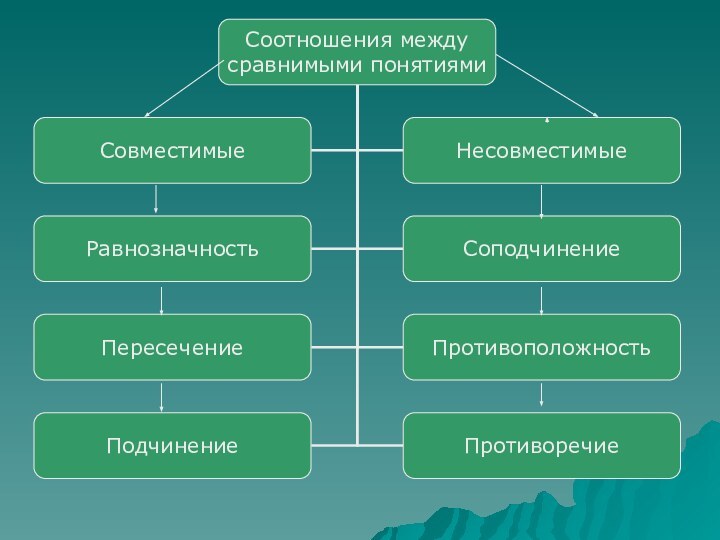
- 45. Среди сравнимых понятий легко выделяются понятия, которые находятся в отношении совместимости и несовместимости
- 46. Совместимые понятия — те, объемы которых полностью
- 47. Несовместимыми понятиями (понятия, находящиеся в отношении несовместимости)
- 49. Отношение между элементом и логическим классом
- 50. Связь объема и содержания понятия выражается определенным
- 51. Закон обратного отношения между объемом и содержанием
- 53. Сравнимые совместимые понятия: Тождество Х – Ю.А. Гагарин, У- первый космонавтХ, У
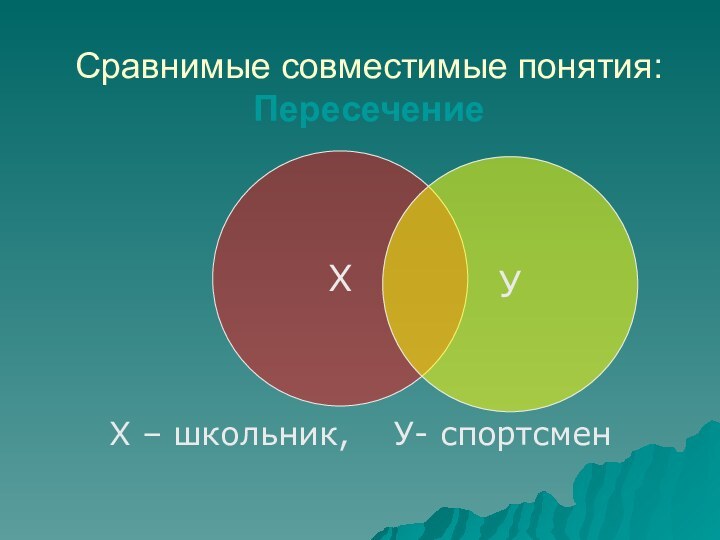
- 54. Сравнимые совместимые понятия: Пересечение Х – школьник, У- спортсменХУ
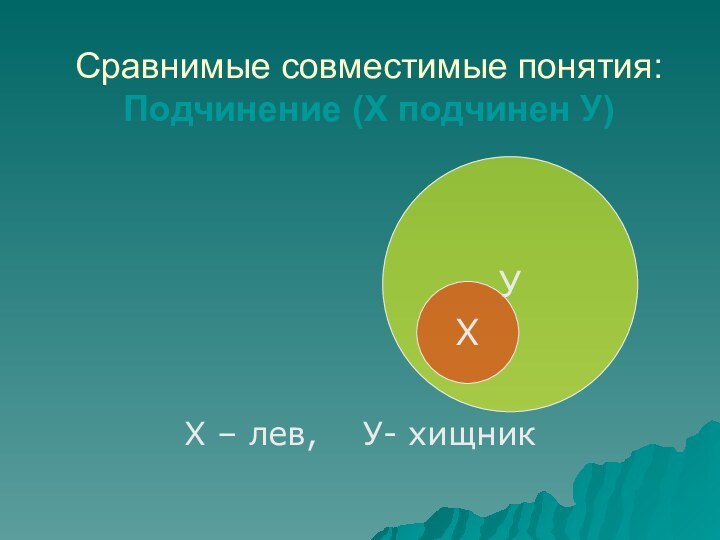
- 55. Сравнимые совместимые понятия: Подчинение (Х подчинен У) Х – лев, У- хищникУХ
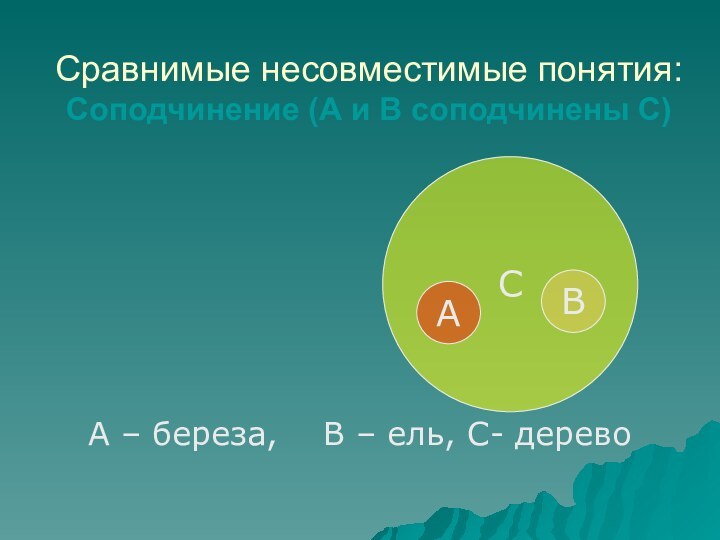
- 56. Сравнимые несовместимые понятия: Соподчинение (А и В
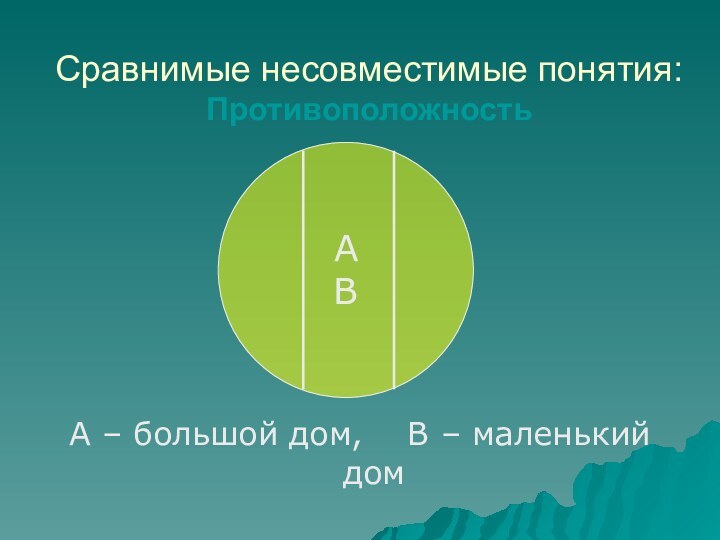
- 57. Сравнимые несовместимые понятия: Противоположность А – большой
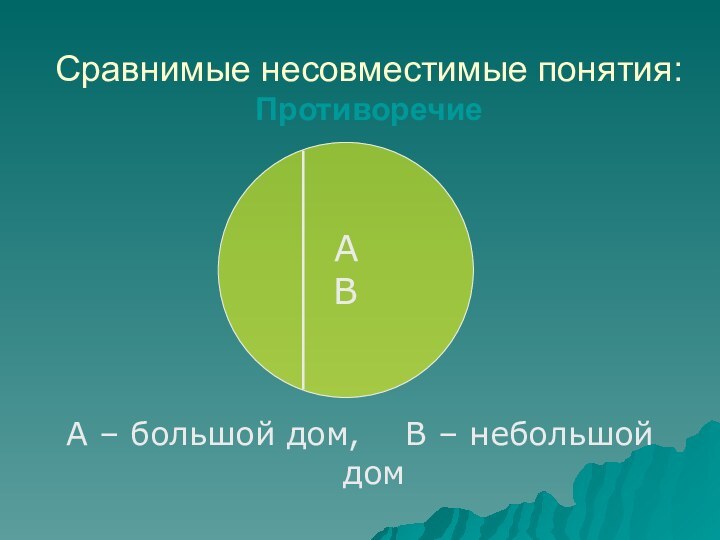
- 58. Сравнимые несовместимые понятия: Противоречие А – большой
- 59. ОПЕРАЦИИ С ПОНЯТИЯМИ К операциям с понятиями
- 60. Операции - самая важная (порой и самая
- 61. Вопросы и задания:Приведите примеры понятий, суждений, умозаключений
- 62. Ответы:2. а) Квинтэссенция – самое главное, наиболее
- 63. Вопросы и задания:Определите объемы понятий:Столица России;Столица,Город,Знаменитый полководец,Бесконечность,Змей
- 64. Вопросы и задания:Выведите, если возможно, заключение из
- 65. Ответы:4) Тем, кто лыс, расческа не нужна.
- 66. Ответы:4) b) Ни один добрый поступок не
- 67. Ответы:4) с) Некоторые уроки трудны. Все что
- 68. ЗаданиеИзучить различные логические операции с понятиямиПодготовить собственные примеры, иллюстрирующие данные операции
- 69. Скачать презентацию
- 70. Похожие презентации
Понятие как форма мышления. Содержание и объем понятия.Виды понятий. Отношения между понятиями.





























































Слайд 2
Понятие как форма мышления. Содержание и объем понятия.
Виды
понятий. Отношения между понятиями.
Слайд 3 Понятие – это логическая мысль о
предмете, отражение предмета в одном или нескольких существенных признаках
Слайд 4 Признак предмета – это то, в чем
предметы сходны друг с другом или чем они друг
от друга отличаются.Слайд 5 Существенные признаки- это необходимо принадлежащие предмету
признаки, выражающие его внутреннюю природу, его сущность
Слайд 6 Несущественные признаки – могут принадлежать или не
принадлежать предмету и которые не выражают его сущности
Слайд 7 Предмет- это конкретные вещи, явления процессы, существовавшие,
существующие или возможные в будущем, а также их свойства,
связиСлайд 8 Понятия образуются на основе представлений образов предметов и
явлений действительности, а также их признаков, являясь их обобщением.
На основе понятий создаются идеальные (идеализированные) аналоги, модели предметов и явлений действительности.
Слайд 9 Материальным носителем понятия выступает слово или сочетание
слов естественного языка: «дом», «человек» или словосочетание: «столица государства»,
«гражданское общество»Слайд 10 Слова, закрепленные за понятиями (имена понятий) в
сложившихся областях практики и научного познания называются терминами.
Слайд 11 К числу основных способов образования понятий
относят:
Анализ
Синтез
Сравнение
Абстрагирование
Обобщение
Слайд 12 Анализ –мысленное расчленение предметов на их
составные части, мысленное выделение в них признаков
Слайд 13 Синтез – мысленное соединение в единое
целое частей предмета и его признаков, полученных в процессе
анализа.Слайд 14 Сравнение –мысленное установление сходства или различия
предметов по существенным и несущественным признакам
Слайд 15 Абстрагирование –мысленное выделение одних признаков предмета
и временное отвлечение от других
Слайд 17 Анализ, синтез, сравнение, абстрагирование, обобщение – логические
приемы, которые взаимосвязаны и образуют единый процесс. Его результат
– мысль, содержание которой бесконечно разнообразно, но форма неизменно одна – понятие.
Слайд 18
Логическая структура понятия
Важнейшими логическими характеристиками всякого понятия
являются его содержание и объем
Слайд 19 Содержание понятия – это совокупность существенных
признаков предмета или класса однородных предметов, отраженных в понятии
Слайд 20 Так в содержании понятия "логика" - наука о
законах и формах правильного мышления, можно выделить признаки "быть
наукой", "быть связанным с мышлением" - общие признаки, неотличительные, "изучать законы и формы мышления" - еще один неотличительный признак, хотя и менее общий. Наконец, "изучать правильное мышление" (как это было определено выше) - отличительный признак. Эти признаки являются существенными в отношении логики как науки.Слайд 22 Так объемом понятия "дом" являются все дома, которые
только мыслит человек. Элементами являются при этом отдельно взятые
конкретные дома, например, Дом Правительства. Подклассами являются некоторые разновидности домов - кирпичные дома, панельные дома, одноэтажные или многоэтажные дома, и т.д.
Слайд 23
Виды понятий:
а) по количественному признаку (по объему):
единичные,
общие, регистрирующие (нулевые исчислимые), нерегистрирующие (неисчислимые )
б) по качественному
признаку (по содержанию):утвердительные, конкретные, соотносительные , собирательные,
отрицательные, абстрактные, безотносительные, разделительные
Слайд 24
по количественному признаку (по объему)
единичные
общие,
регистрирующие (нулевые исчислимые),
нерегистрирующие
(неисчислимые )
Слайд 25 Единичными понятиями являются те, которые отражают всего
лишь один единственный предмет (явление, процесс), т.е. объем этих
понятий индивидуален. Это, например, понятия о дневном светиле, об авторе «Мастера и Маргариты»Слайд 26 Общими понятиями являются те, в которых мыслится
множества предметов.
Общее понятие в грамматической форме может выражаться
и единственным числом; в логике слова «стол» и «столы» одинаково выражают общее понятие о столе. Слайд 27 Пустые (нулевые) понятия — это понятия,
объемы которых отражают пустые предметные области, им не соответствуют
никакие реальные объекты; предметная область которых равна нулю. Понятия о сказочных или фантастических, мифологических объектах тоже являются пустыми понятиями («сирена», «русалка», «конек-горбунок», «минотавр» и пр.).Слайд 28 Регистрирующие (исчислимые) понятия —отражают поддающуюся исчислению область (множество,
класс) предметов. Например, «дни недели», «времена года» и пр.
Слайд 29 Нерегистрирующие (неисчислимые) — все те понятия, объемы которых
фактически не поддаются точному исчислению. Это такие предельно широкие
понятия, как «количество», «качество», «мера» и пр., такие общие понятия, как «дерево», «река», «человек» и пр., абстрактные понятия «белизна», «кривизна» и др.
Слайд 30
по качественному признаку (по содержанию)
утвердительные,
конкретные,
соотносительные,
собирательные,
отрицательные,
абстрактные,
безотносительные,
разделительные
Слайд 31 Утвердительными (положительными) понятиями являются те, которые отражают наличие
какого-то признака у предмета. Положительными понятиями могут быть как
общие. так и единичные, пустые. «Проницательность», «грамотные люди», «сказочные герои».Слайд 32 Отрицательные понятия указывают на отсутствие любого признака, утверждаемого
положительным понятием; формируются они простым прибавлением к любому положительному
понятию частицы «не»: «не-роза», «не-студент» и пр. Общеупотребимое понимание отрицательности не всегда совпадают с логическим.Слайд 33 Собирательные понятия специфичны, специфичны потому, что содержанием своим
отражают определенное (строгое или не строгое) количество однородных предметов
как нечто целое, например: «созвездие», «учебный класс», «группа», «взвод», «Волосы Вероники» и т. п.Слайд 34 Разделительные понятия — понятия, содержанием своим относимые к
каждому в отдельности предмету множества (группы, класса), например: «всякий»,
«каждый» и пр.Слайд 35 Конкретными понятиями являются те, которые отражают предмет (явление,
процесс) в целом: «ночь», «улица», «фонарь». «аптека» и т.п.
Конкретными понятиями могут быть любые утвердительные как общие, так и единичные, и даже пустые понятия.Слайд 36 Абстрактными в логике считаются те понятия, которые отражают
отдельное свойство предмета, отдельный его признак, и отражают его
так, как будто бы он существуют независимо от своего предмета-носителя, например: «белизна», «крутизна», «человечность», «вечность» и пр.Слайд 37 Соотносительными понятиями в логике считаются те, которые содержанием
своим требуют обязательного соотношения, соотнесения с другими понятиями, например:
«копия», «больше», «хуже», «между» и др.Слайд 38 Безотносительными понятиями являются все те, которые мыслятся сами
по себе, без обязательного соотнесения их с другими. Такими
понятиями могут быть и утвердительные, и отрицательные, и конкретные, и абстрактные, и общие, и единичные, и др., кроме соотносительных.
Слайд 39
ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
Виды понятий находятся между
собой в определенных отношениях, и прежде всего в отношении
сравнимости и несравнимости.Слайд 40 В отношении сравнимости находятся те понятия, в объеме
или содержании которых имеется что-то общее: «человек» и «студент»,
«право» и «мораль».Слайд 44 В отношении несравнимости находятся те понятия, ни в
объеме ни в содержании которых нет ничего общего: «атом»
и «совесть», «любовь» и «чернильница»Слайд 45 Среди сравнимых понятий легко выделяются понятия, которые находятся
в отношении совместимости и несовместимости
Слайд 46 Совместимые понятия — те, объемы которых полностью или
частично совпадают: «студент», «учащийся», «спортсмен». В логике часто опираются
только на один из этих элементов - на объем, поскольку он более прост и выразителен при формальном анализе понятий.Слайд 47 Несовместимыми понятиями (понятия, находящиеся в отношении несовместимости) —
являются те, объемы которых полностью не совпадают, а отдельные
содержательные признаки исключают друг друга: «судья» — «прокурор», «зеленый» — «красный» и т. п.Слайд 49 Отношение между элементом и логическим классом называется принадлежностью
элемента классу: а А ("где А - класс, а
- элемент, - символ отношения принадлежности). Отношение между классом и его подклассом называется включением класса в класс: В А (где А - класс, В - подкласс, - символ включения подкласса в класс).Слайд 50 Связь объема и содержания понятия выражается определенным законом
- законом обратного отношения между объемом и содержанием понятия.
Слайд 51 Закон обратного отношения между объемом и содержанием понятия
- это закон, согласно которому, чем больше объем понятия,
тем меньше его содержание, и наоборот, чем меньше объем понятия, тем больше его содержание.
Слайд 56
Сравнимые несовместимые понятия:
Соподчинение (А и В соподчинены С)
А
– береза, В – ель, С- дерево
С
А
В
Слайд 59
ОПЕРАЦИИ С ПОНЯТИЯМИ
К операциям с понятиями (или
над понятиями) относят отрицание, умножение, сложение, вычитание, обобщение, ограничение,
деление и определение.Слайд 60 Операции - самая важная (порой и самая сложная)
часть учения о понятии, затрагивающая либо один элемент понятия,
либо оба сразу.
Слайд 61
Вопросы и задания:
Приведите примеры понятий, суждений, умозаключений из
курсов математики, русского языка, информатики.
Перечислите существенные признаки, составляющие содержание
понятий:Квинтэссенция;
Добродетель,
Истина,
Ложь.
(Пояснение: посмотрите толковый словарь)
(ОТВЕТ)
Слайд 62
Ответы:
2. а) Квинтэссенция – самое главное, наиболее существенное
в тексте, рассуждении.
b) Относится к области этики, нравственности; является
положительным нравственным качеством; рассматривается как цель, к которой надо стремиться в отношениях с окружающими.Основная цель познания, то, что существует в действительности; утверждение, суждение, подтвержденное практикой, опытом.
Противоположность истине; утверждение, не соответствующее действительности.
Слайд 63
Вопросы и задания:
Определите объемы понятий:
Столица России;
Столица,
Город,
Знаменитый полководец,
Бесконечность,
Змей Горыныч.
(Пояснение:
единичное, общее, пустое)
Ответы:
a) единичное
b) общее
с) общее
d) общее
e) единичное
f) пустое
Слайд 64
Вопросы и задания:
Выведите, если возможно, заключение из каждой
пары посылок:
Тем, кто лыс, расческа не нужна.
Ни одна ящерица
не имеет волос. (Ответ)Ни один добрый поступок не является незаконным. Все что законно, можно делать без страха. (Ответ)
Некоторые уроки трудны. Все что трудно, требует внимания. (Ответ)
Слайд 65
Ответы:
4) Тем, кто лыс, расческа не нужна.
Ни одна
ящерица не имеет волос.
а) Суждения:
А = некто имеет волосы;
В
= некто нуждается в расческе;С = некто – ящерица.
Умозаключение:
Если не А, то не В.
Если С, то не А.
Если С, то не В.
Ни одной ящерице расческа не нужна.
Слайд 66
Ответы:
4) b) Ни один добрый поступок не является
незаконным. Все что законно, можно делать без страха.
Суждения:
S =
совершать добрый поступок;M = поступать законно;
P = испытывать страх.
Умозаключение:
Ни один S не есть не M.
Все М есть не Р.
Все S есть не Р.
Все добрые поступки можно делать без страха.
Слайд 67
Ответы:
4) с) Некоторые уроки трудны.
Все что трудно, требует
внимания.
Суждения:
S = урок;
M = быть трудным;
P = требовать внимания.
Умозаключение:
Некоторые
S есть M.Все М есть Р.
Некоторые S есть Р.
Некоторые уроки требуют внимания.





























