- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Золотое сечение
Содержание
- 2. ВведениеЧеловек различает окружающие его предметы по форме.
- 3. ВведениеЦелое всегда состоит из частей, части разной
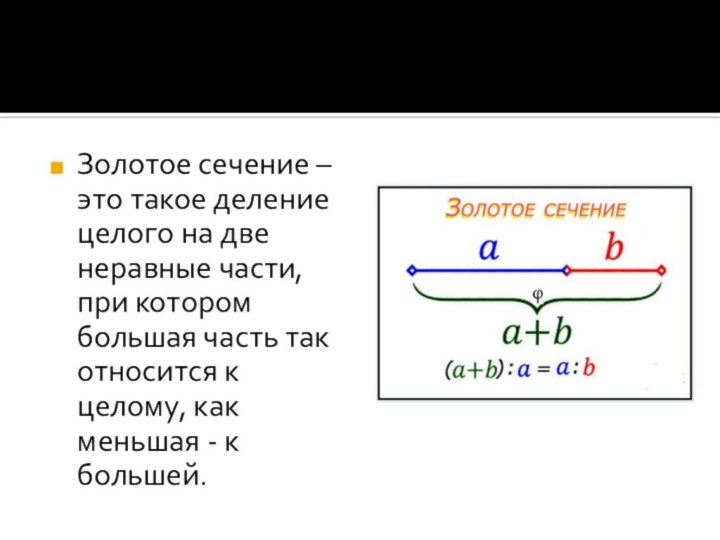
- 4. Золотое сечение – это такое деление целого
- 5. Немного историиДревнейшим литературным памятником, в котором встречается
- 6. Немного историиНо ещё Пифагор и его ученики
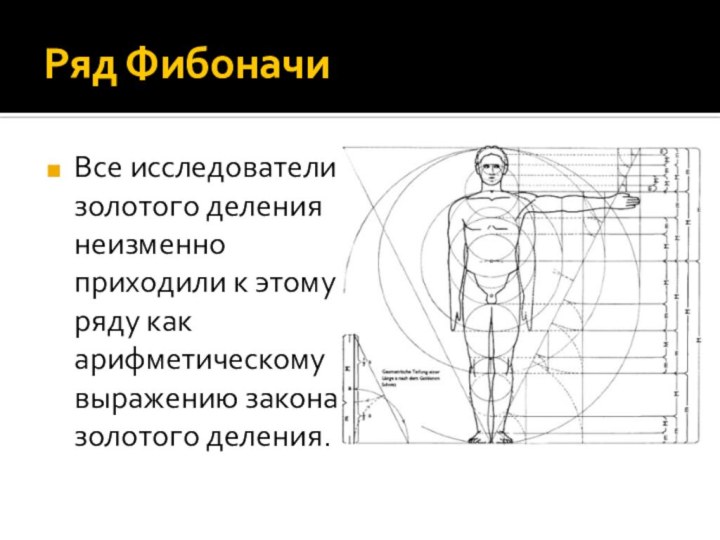
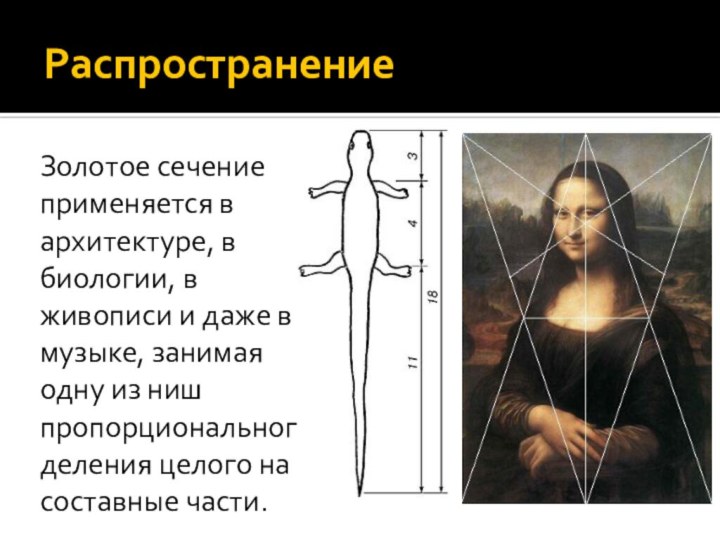
- 7. Ряд ФибоначиС историей золотого сечения косвенным образом
- 8. Ряд ФибоначиВыведенный им ряд чисел 0, 1,
- 9. Ряд ФибоначиЭто отношение обозначается символом Ф. Только это
- 10. Ряд ФибоначиВсе исследователи золотого деления неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
- 11. Ряд ФибоначиЗакономерности «золотой» симметрии проявляются в строении
- 12. Золотое сечение и симметрияЗолотое сечение нельзя рассматривать
- 13. Скачать презентацию
- 14. Похожие презентации
ВведениеЧеловек различает окружающие его предметы по форме. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии.










Слайд 3
Введение
Целое всегда состоит из частей, части разной величины
находятся в определенном отношении друг к другу и к
целому.Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.