Презентация на тему Электротехника и электроника. Резонанс. Лекция № 7

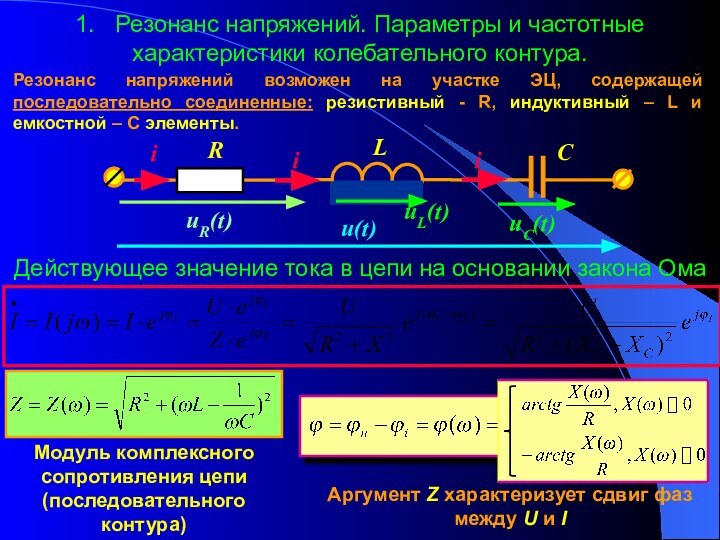
характеристики колебательного контура.
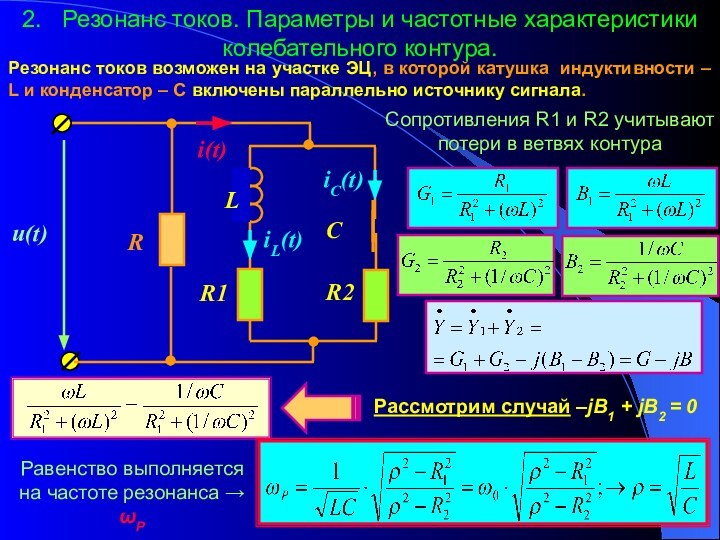
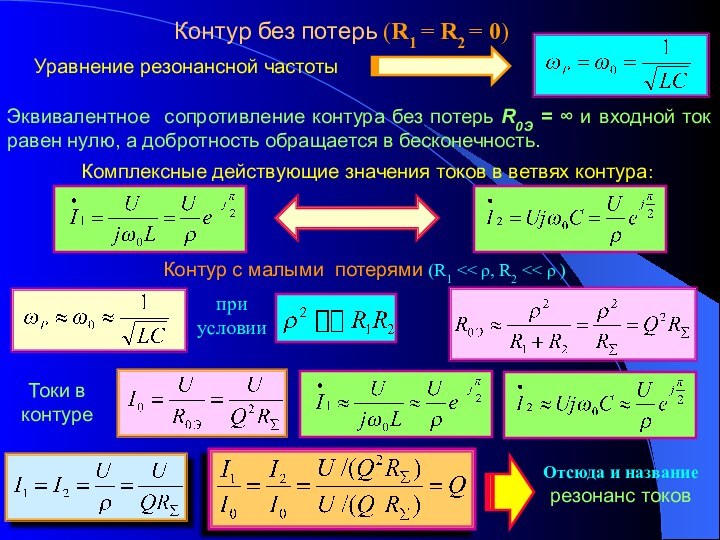
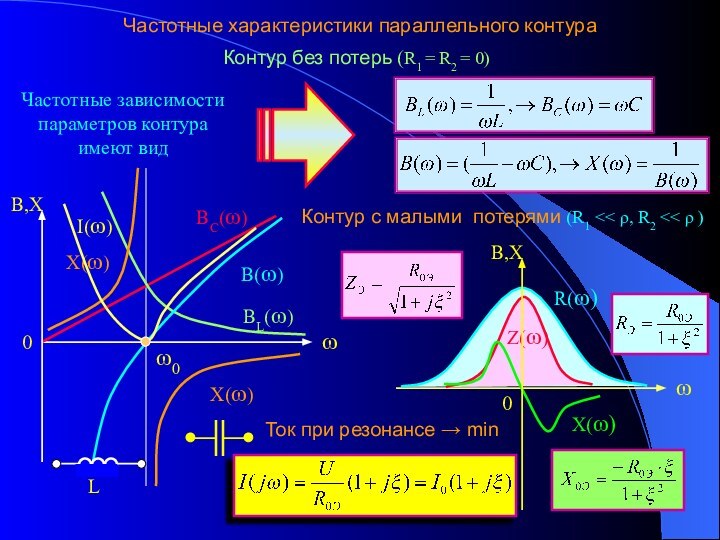
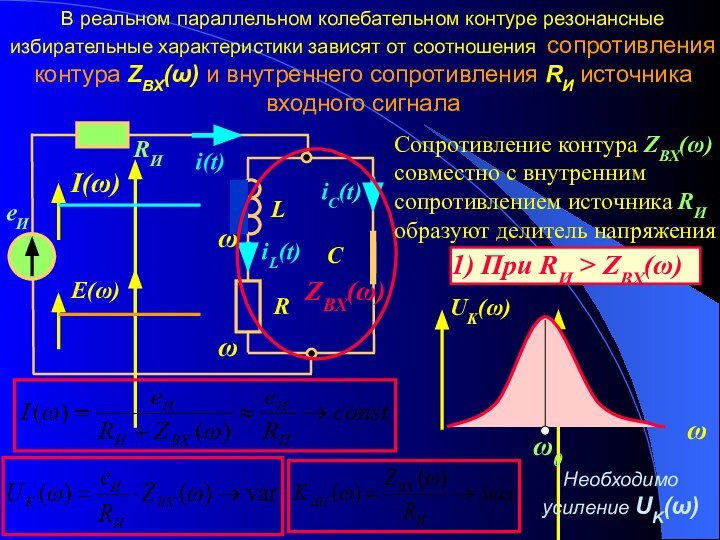
2. Резонанс токов. Параметры и частотные характеристики

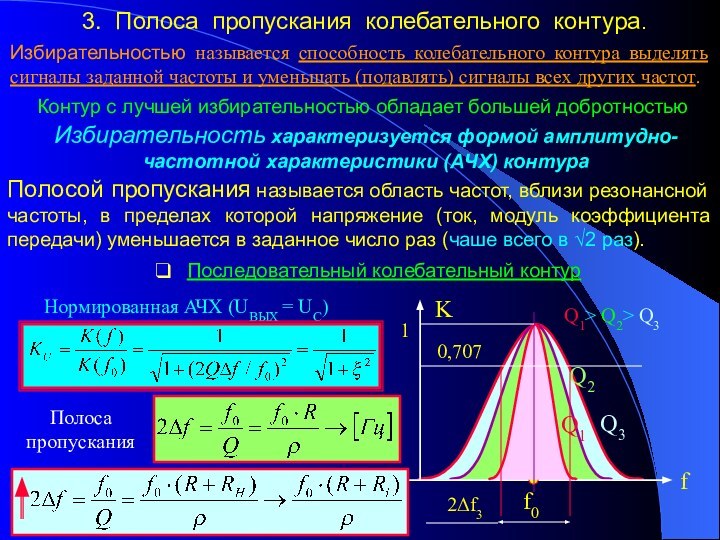
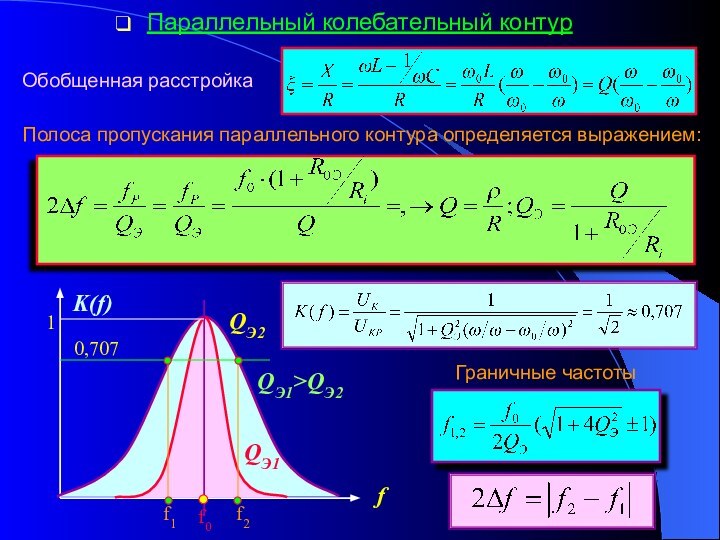
3. Полоса пропускания колебательного контура.

Литература:

1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 105 – 113

2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 54 – 66.

3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.: Высшая школа, 2003 г, с. 37 –83.

колебательного контура.
Резонанс напряжений возможен на участке ЭЦ, содержащей последовательно

Действующее значение тока в цепи на основании закона Ома

Модуль комплексного сопротивления цепи (последовательного контура)

Аргумент Z характеризует сдвиг фаз между U и I

резистивный - R, индуктивный – L и емкостной –

При резонансе ϕ = 0, если Х = ХL – XC = ωL –1/ ωC = 0, что может быть выполнено лишь для некоторой частоты ω = ω0. В этом случае

В последовательном контуре из токов с различными частотами выделяется ток, только одной определенной частоты

Частота входного напряжения при которой наступает резонанс, обозначается ω0 и называется резонансной или собственной частотой последовательного колебательного контура.

другу.
Характеристическое (волновое) сопротивление контура
Резонансные свойства (избирательность) контура

Пример: Пусть U=

Значение тока на резонансной частоте

Добротность показывает, во сколько раз резонансные напряжения на реактивных элементах превышают приложенное напряжение (напряжение источника входного сигнала) ⇒ термин «резонанс напряжений»

токов в RLC цепи показывает, что они все являются

XL(ω), XC (ω), X(ω), Z(ω) ⇒ частотные характеристики цепи,
ϕ(ω) ⇒ фазочастотная характеристика цепи

XL(ω)

ω0

С

и напряжений на реактивных элементах контура.
Зависимости I(ω), UL (ω),

Экстремумы на частоте

Для нахождения экстремумов UL (ω), UC (ω) необходимо:

элементах контура примут максимальное значение.
С увеличением добротности контура (уменьшением

колебательного контура.
Резонанс токов возможен на участке ЭЦ, в которой

Сопротивления R1 и R2 учитывают потери в ветвях контура

Рассмотрим случай –jB1 + jB2 = 0

Равенство выполняется на частоте резонанса → ωР

в неразветвленной части цепи
R0Э – эквивалентное резонансное сопротивление контура
Режим

При этом эквивалентное резонансное сопротивление параллельного контура

Наибольший теоретический и практический интерес представляют резонанс токов в контурах без потерь (R1 = R2 = 0) и с малыми потерями (R1 << ρ, R2 << ρ )

Уравнение резонансной частоты

Эквивалентное сопротивление контура без потерь R0Э =

Комплексные действующие значения токов в ветвях контура:

Контур с малыми потерями (R1 << ρ, R2 << ρ )

при условии

Токи в контуре

Отсюда и название резонанс токов

R2 = 0)
Частотные зависимости параметров контура имеют вид

Контур

Ток при резонансе → min

зависят от соотношения сопротивления контура ZВХ(ω) и внутреннего сопротивления

Сопротивление контура ZВХ(ω) совместно с внутренним сопротивлением источника RИ образуют делитель напряжения

1) При RИ > ZВХ(ω)

ω0

Необходимо усиление UK(ω)

сигнала нет
Параллельный колебательный контур включают в цепи, обладающие

контура выделять сигналы заданной частоты и уменьшать (подавлять) сигналы

Контур с лучшей избирательностью обладает большей добротностью

Избирательность характеризуется формой амплитудно-частотной характеристики (АЧХ) контура

Полосой пропускания называется область частот, вблизи резонансной частоты, в пределах которой напряжение (ток, модуль коэффициента передачи) уменьшается в заданное число раз (чаше всего в √2 раз).

Последовательный колебательный контур

Нормированная АЧХ (UВЫХ = UC)

0,707

1

Q1> Q2> Q3

Полоса пропускания

контура определяется выражением:
QЭ1>QЭ2
Граничные частоты

существенно расширить полосу пропускания контура, не изменяя его резонансной

Практически часто уменьшают добротность за счет увеличения активного контура двумя путями:
введением в контур добавочного сопротивления RД;
шунтированием контура резистором RШ.

Сопротивление добавочного резистора рассчитывают по формуле

Подключение к контуру шунтирующего резистора RШ эквивалентно включению последовательно с элементами контура добавочного резистора RД