на траектории;
положительное направление отсчета;
закон изменения дуговой координаты:
s
= s(t)О
−
+
М
s(t)
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







О
−
+
М
s(t)
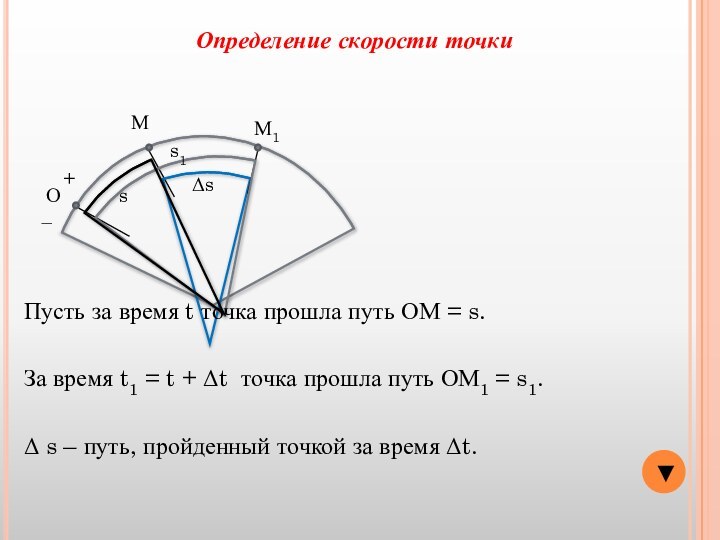
Δ s – путь, пройденный точкой за время Δt.
▼
Эти оси направлены следующим образом:
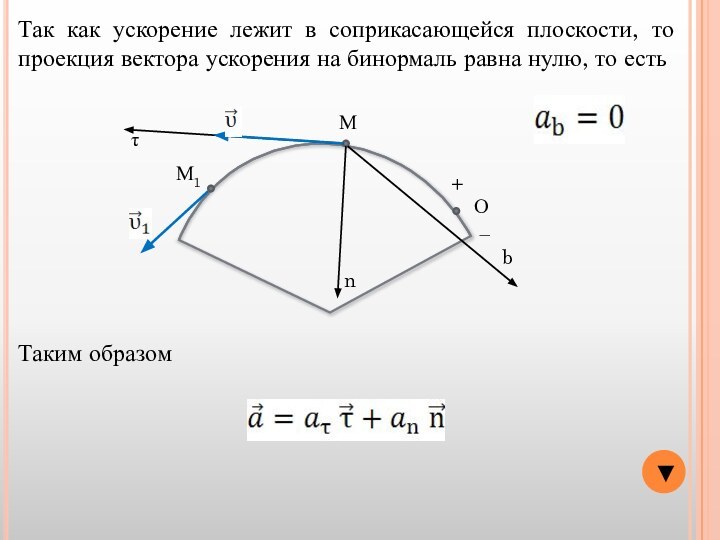
n
Ось Мb перпендикулярна к первым двум и направлена так, чтобы она образовывала с ними правую тройку.
b
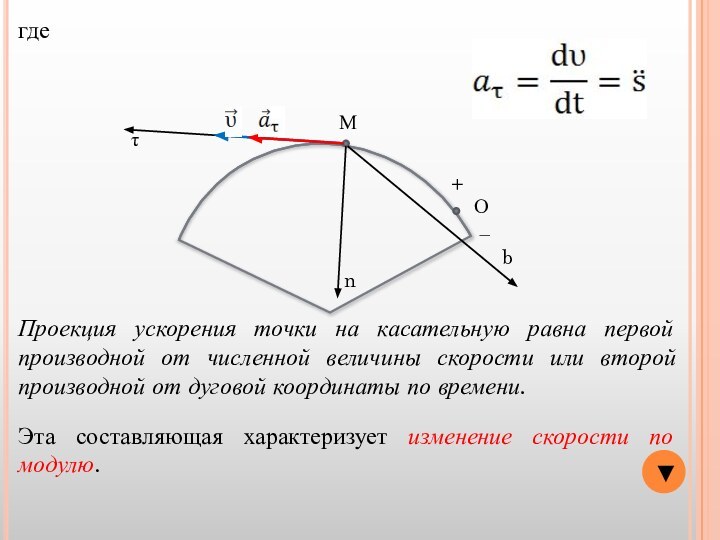
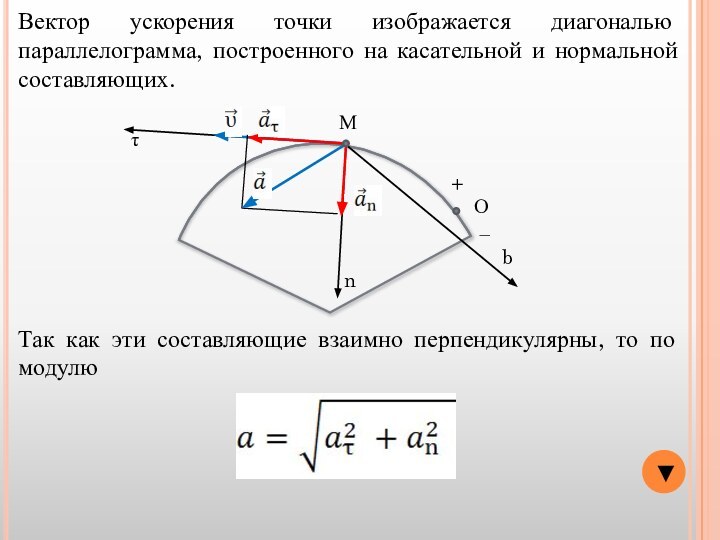
Эта составляющая характеризует изменение скорости по модулю.
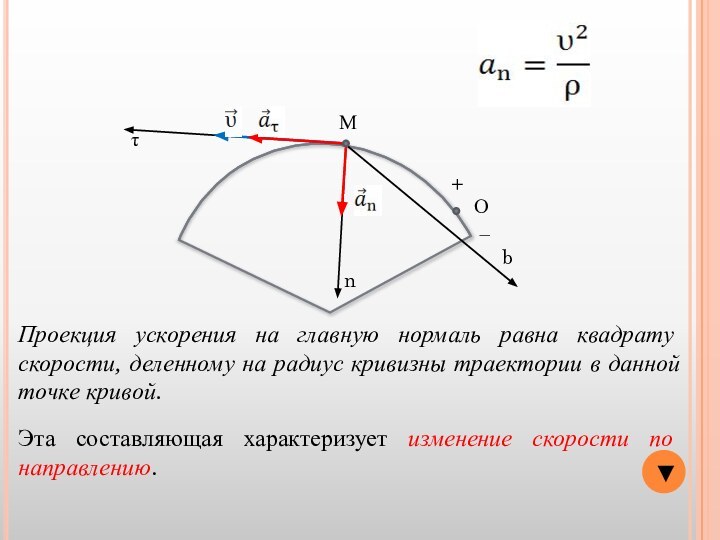
Эта составляющая характеризует изменение скорости по направлению.