Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Пространственная система сил

Содержание

2. Пусть силы
3. (3)Модули главного вектора и главного момента
4. В случае равновесия произвольной пространственной системы сил
5. Вывод. Для равновесия произвольной пространственной системы сил
6. Тогда проекции каждой из сил на оси
7. Вывод. Для равновесия пространственной системы параллельных сил
8. Однородная прямоугольная плита весом Р = 5
9. Усилие в невесомом стержне СС / -
10. 4. Составим уравнения равновесия.А) Уравнения проекций.Предварительно, в
11. В) Уравнения моментов.(4)(5)(6)
12. Скачать презентацию
13. Похожие презентации

Пусть силы заданы аналитически, т.е. известны проекции сил на оси координат:

Главная
Физика
Пространственная система сил

С Т А Т И К А10. Пространственная система сил

(3)Модули главного вектора и главного момента Проекции главного момента - по

В случае равновесия произвольной пространственной системы сил главный вектор и главный момент

Вывод. Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы

Тогда проекции каждой из сил на оси Ох и Оу и их

Вывод. Для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы сумма

Однородная прямоугольная плита весом Р = 5 кН со сторонами АВ =

4. Составим уравнения равновесия.А) Уравнения проекций.Предварительно, в целях применения теоремы Вариньона о

4. Решение системы уравнений (1) – (6). Из уравнения (2) найдем УА=

Слайды презентации

Слайд 2 Пусть силы

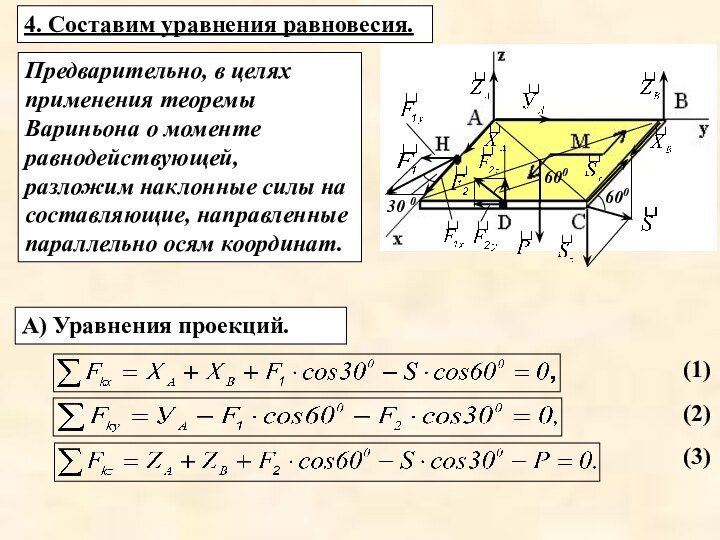
заданы аналитически, т.е. известны проекции сил на оси координат: F1х ,F2х , …,Fnх; F1у , F2у , …,Fnу ; F1z , F2z , …, Fnz .

Главный момент системы сил относительно центра О -

Теорема о приведении системы сил:
Любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой

, равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом

10.1.Вычисление модулей главного вектора и главного момента

Главный вектор системы сил

равным главному моменту системы сил относительно центра О.

Слайд 3 (3)
Модули главного вектора и главного момента
Проекции

(3)Модули главного вектора и главного момента Проекции главного момента -

главного момента - по формулам
Rх = ∑ Fкх ,

Rу = ∑ Fку , Rz = ∑ Fкz . (1)

Тогда проекции главного вектора на оси координат определятся по формулам

Слайд 4 В случае равновесия произвольной пространственной системы сил главный

вектор и главный момент равны нули, то есть
10.2.Условия

равновесия произвольной пространственной системы сил

Следовательно, равны нулю и их модули:

то есть

(4)

Так как подкоренные выражения не могут быть отрицательными, то условия (4) могут выполнятся только в случаях, если

Rх = 0 , Rу = 0, Rz = 0 . (5)

Слайд 5 Вывод. Для равновесия произвольной пространственной системы сил необходимо

Вывод. Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы

и достаточно, чтобы суммы проекций всех сил на каждую

из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.

∑ Fкх = 0 ,
∑ Fку = 0 ,
∑ Fкz = 0,

или, с учетом формул (1) и (2)

МОх = 0, МОу = 0, МОz= 0 . (6)

Слайд 6
Тогда проекции каждой из сил на оси Ох

Тогда проекции каждой из сил на оси Ох и Оу и

и Оу и их моменты относительно оси Оz будут

равны нулю и система (7) даст три условия равновесия:

10.3. Случай параллельных сил

Если все действующие силы параллельны друг другу,

то можно выбрать координатные оси так, что ось Оz , будет параллельна силам.

∑ Fкz = 0,

Остальные равенства обратятся в тождества (0 ≡ 0).

Слайд 7 Вывод. Для равновесия пространственной системы параллельных сил необходимо

Вывод. Для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы

и достаточно, чтобы сумма проекций всех сил на ось

параллельную силам, и сумма их моментов относительно двух других координатных осей были равны нулю.

10.4. Пример решения задач на равновесие произвольной пространственной системы сил.

Слайд 8 Однородная прямоугольная плита весом Р = 5 кН

со сторонами АВ = 4а, ВС = 3а

закреплена в точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СС′.

На плиту действуют пара сил с моментом М = 5кН⋅м, лежащая в плоскости плиты, и две силы:

F1= F2= 2 кН.

Определить реакции связей в точках А, В и С. Принять а = 0,8м.

Сила F1 лежат в плоскости, параллельной плоскости ху, а сила F2 – в плоскости, параллельной хz. Точки приложения сил (D, H) находятся в серединах сторон плиты.