Презентация на тему Процесс многократного рассеяния

Z1 + Z2
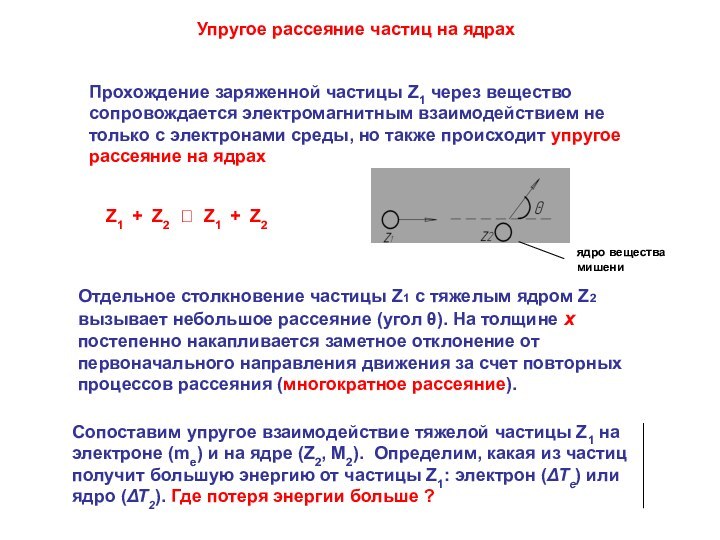
Отдельное столкновение частицы Z1 с тяжелым ядром

Сопоставим упругое взаимодействие тяжелой частицы Z1 на электроне (me) и на ядре (Z2, M2). Определим, какая из частиц получит большую энергию от частицы Z1: электрон (ΔΤе) или ядро (ΔΤ2). Где потеря энергии больше ?

Прохождение заряженной частицы Z1 через вещество сопровождается электромагнитным взаимодействием не только с электронами среды, но также происходит упругое рассеяние на ядрах

ядро вещества мишени

ядре
Сопоставим упругое взаимодействие тяжелой частицы Z1 на электроне

частица Z1 пролетает мимо электрона и ядра с одинаковым прицельным параметром ρ и с одинаковой скоростью V1

ядре

толстый слой, не должна заметно терять энергию: T1(x =0)

Суммарный угол θ =Σ θi, где θi – рассеяние в i-ом взаимодействии, не может служить мерой рассеяния. Его величина, с учетом знака углов отклонений θi, равна нулю.

Принято оценивать квадратичный угол: = Σ θi2

Для учета взаимодействия частицы Z1 с отдельным ядром i можно использовать формулу Резерфорда

Условия расчета:

столкновения с ядром
Расчет в приближении малых углов - в

Значения предельных углов связаны с размерами ядра (Rяд) и атома (Rат) и зависят от материала вещества-мишени

рассеяния получается как сумма значений по полному числу отдельных

m = σ·n·x

σ(см2) – полное резерфордовское сечение рассеяния
n(1/cм3) – концентрация ядер мишени
Х (см) – толщина мишени

Получается функциональная зависимость вида:

Заряженная частица (Z1), движущаяся с импульсом р1
(скорость v1) через вещество толщиной х,
приобретает среднеквадратичный угол

Точные расчеты дают подобную зависимость:

L - длина взаимодействия

с импульсом р1, попадает в однородное магнитное поле перпендикулярно

Их равенство позволяет вычислить
величину радиуса вращения в магнитном поле

Эта запись справедлива и для релятивистского случая

Получаем: