Презентация на тему Работа и механическая энергия

− это количественная характеристика процесса обмена энергией между взаимодействующими

телами.
Рассмотрим вариант, когда тело движется прямолинейно и на него действует постоянная сила.
Работой A, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения s, умноженному на косинус угла α между векторами силы и перемещения:

Работа – скалярная величина (число):
может быть как положительной (0° ≤ α < 90°),
так и отрицательной (90° < α ≤ 180°);
при α = 90° работа, совершаемая силой, равна нулю.

В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе A, совершаемой силой F в 1 Н на перемещении s тела на 1 м в направлении действия силы (α = 0°).

+3

случае переменной силы водится понятие элементарной работы δA.
Элементарной работой

δA, совершаемой переменной силой dF, называется физическая величина, равная скалярному произведению векторов силы и элементарного перемещения dr:

dFr − проекция силы dF на касательную к траектории.

Работа, совершаемая силой на конечном участке пути 1−2:

равна сумме элементарных работ δA на отдельных бесконечно малых участках пути dr :

равна сумме элементарных работ ΔAi на отдельных малых участках пути Δsi :

При сильных изменениях силы dF:

+4

движении вокруг оси ОМ.
Воспользуемся тем, что скорость точки

при вращательном движении связана с угловой скоростью вращения соотношением:

Вращение тела вокруг оси ОМ

+9

Лекция 4. Работа и механическая энергия

Работа силы при повороте тела на конечный угол φ:

Тогда перемещение:

Причем момент силы, действующий на тело:

так как смешанное произведение векторов допускает их циклическую перестановку:

Тогда:

Угловая скорость направлена вдоль оси вращения ОМ, значит скалярное произведение векторов:

причем:

проекция момента силы на ось вращения.

Чаще ось обозначают Z:

совершения работы вводят понятие мощности.
Средняя мощность равна работе

за единицу времени:

Мгновенная мощность - мощность в данный момент времени равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.

В Международной системе (СИ) единица мощности называется ватт (Вт).
Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с:

При вращательном движении мощность силы определяется моментом этой силы и угловой скоростью:

и

+4

об изменении кинетической энергии
Вывод: работа силы идет на приращение

некоторой величины (стоящей в скобках), которую называют кинетической энергией тела.
Таким образом, кинетическая энергия − это энергия тела, обусловленная его механическим движением.
Для тела массой m двигающегося поступательно со скоростью кинетическая энергия определяется соотношением:

Кинетическая энергия тела или системы тел - это энергия, которой обладает тело или система вследствие своего движения.

Пусть тело массой m движется поступательно под действием некоторой силы (или результирующей нескольких сил):

на элементарном перемещении

Тогда элементарная работа, которую совершает эта сила на элементарном перемещении:

Приращение кинетической энергии тела при некотором перемещении равно работе результирующей всех сил, действующих на тело на том же перемещении.

Интегрируем от начальной до конечной скорости и получим теорему об изменении кинетической энергии:

+6

вращении тела
При вращательном движении тела скорости точек тела связаны

с угловой скоростью вращения соотношением: vi=ωri, где ri - расстояние от точек тела до оси вращения. Тогда кинетическая энергия тела при вращательном движении:

- момент инерции тела относительно оси вращения Z

где

Любое движение твердого тела может быть представлено как сумма поступательного и вращательного движений.
Как следствие, кинетическая энергия плоского движения тела будет слагаться из кинетической энергии поступательного движения со скоростью v центра масс и энергии вращения вокруг оси, проходящей через центр масс:

+2

и уравнения, определяющие поступательное движение тела и его вращение

вокруг неподвижной оси:

Лекция 4. Работа и механическая энергия

+2

силы
Среди неконсервативных сил выделяют диссипативные и гироскопические силы.
1) Диссипативные силы.

К ним относятся, в частности, силы трения и силы сопротивления среды. Полная работа этих сил является отрицательной.
При наличии сил трения и сопротивления энергия механической системы уменьшается, переходя во внутреннюю энергию тел, что приводит к их нагреванию. Такой процесс называют диссипацией энергии, а силы называют диссипативными.
2) Гироскопические силы. Эти силы зависят от скорости движения материальной точки и действуют перпендикулярно к этой скорости. Работа таких сил всегда равна нулю, однако от консервативных сил они отличаются тем, что определяются не только положением точки, но и ее скорости.
Примером такой силы является сила Лоренца. Сила Лоренца − это сила, действующая на заряженную частицу q, движущуюся со скоростью v, в магнитном поле с индукцией B:

Все силы в механике делятся на:

Консервативные силы

Неконсервативные силы

Силы, работа которых не зависит от формы траектории, а зависит только от начального и конечного положения движущейся точки.

Силы, работа которых зависит от формы траектории, описываемой точкой приложения силы.

их работа по замкнутому контуру равна нулю

их работа по замкнутому контуру не равна нулю

Примеры таких сил: тяготения, тяжести, упругости, электростатические и др., которые являются центральными.

+6

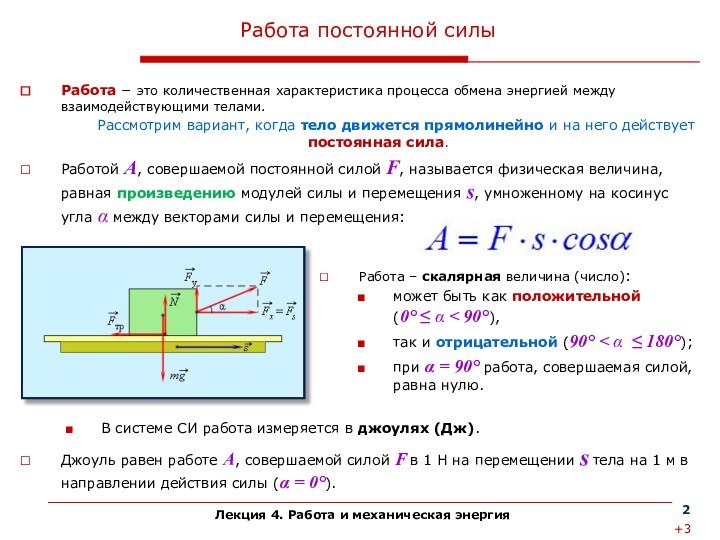
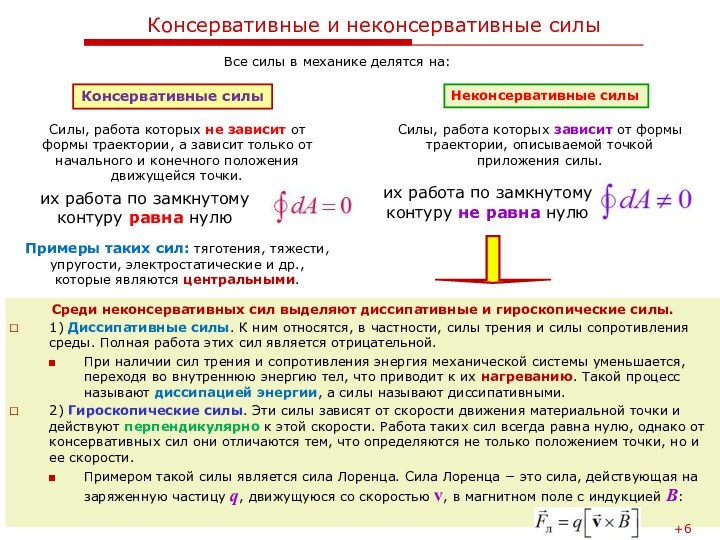
и потенциального поля
Потенциальная энергия П (или Wp) - часть

общей механической энергии системы, зависящей от взаимного расположения материальных точек системы и их положения во внешнем силовом поле.
Из определения следует, что потенциальная энергия системы не должна зависеть от того, каким образом данная конфигурация частиц системы возникла.
Это значит, что понятие потенциальной энергии имеет смысл лишь в том случае, когда на материальные точки системы действуют только консервативные силы.
Изменение потенциальной энергии системы должно определяться только работой консервативных сил. Другими словами, работа консервативных сил при переходе из состояния 1 в состояние 2 равна убыли потенциальной энергии: А=-(П2-П1)=-ΔП

Таким образом, силовое поле консервативных сил является потенциальным полем.
Поле силы – это область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке.
Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа).
Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.
Потенциальное поле – это стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек.
Силы потенциального поля обязательно консервативные. Если это условие не выполняется, то силовое поле не является потенциальным.
Силовое поле представляет собой особую форму существования материи, посредством которой осуществляются гравитационное, электромагнитное, ядерное и другие взаимодействия.

+4

и энергией потенциального поля
Взаимодействие в консервативной системе может быть

описано с помощью потенциальной энергии П либо с помощью сил F взаимодействия точек системы.
Поэтому между потенциальной энергией и силой, действующей на материальную точку, должна существовать определенная взаимосвязь.
Потенциальная энергия системы является функцией координат П(x, y, z).

Градиент П − это вектор, направленный по нормали к эквипотенциальной поверхности в сторону возрастания потенциальной энергии П.
Вектор силы F направлен в сторону уменьшения П и противоположен по направлению вектору gradП .

Пусть силы, действующие на систему, выполнили элементарную работу:

С другой стороны:

Сравнивая выражения, получим выражения для проекций сил поля:

Для вектора силы получаем следующее выражение:

Эквипотенциальная поверхность − поверхность, во всех точках которой потенциальная энергия П имеет одно и то же значение.

+4

энергии: гравитационная сила
Найдем потенциальную энергию тела массы m,

находящегося в гравитационном поле Земли.
На тело действует гравитационная сила притяжения, направленная к центру Земли Учитывая направление силы, ее вектор можно записать в виде:

где М - масса Земли, r - радиус-вектор, направленный от центра Земли к телу.

Пусть тело перемещается по произвольному пути от точки 1 до точки 2.
Работа гравитационной силы по перемещению тела:

Но работа А=-ΔП.
Поэтому потенциальная энергия гравитационных сил:

+3

энергии: сила упругости и сила тяжести
Найдем потенциальную энергию тела

массы m, находящегося в поле силы упругости (пружины).
Для этого рассмотрим колебания пружины вдоль оси х и вычислим работу силы упругости при деформации пружины от х1 до х2. Учитывая, что сила упругости направлена в сторону, противоположную деформации, элементарная работа силы упругости:

где Fx=-kx - проекция силы упругости на ось х, r - радиус-вектор, направленный по оси х.

Пусть тело перемещается по пути от точки 1 до точки 2. Работа силы упругости по перемещению тела:

Но работа А=-ΔП. Поэтому потенциальная энергия сил упругости:

Сила тяжести. Найдем потенциальную энергию тела, находящегося в поле силы тяжести Земли. Работа силы тяжести (F=mg) по перемещению тела из точки 1 в точку 2:

Поэтому потенциальная энергия силы тяжести:

где h - высота тела над поверхностью Земли.

+4

энергии
Пусть на материальные точки системы действуют только консервативные силы.

Тогда при переходе системы из одного состояния работа консервативных сил равна:
А=К2-К1 или А=-(П2-П1).
Тогда К2-К1 =-(П2-П1), значит: К2+П2=К1+П1=const

Величину E = К + П называют полной механической энергией системы.
Отсюда следует закон сохранения полной механической энергии: полная механическая энергия системы, на материальные точки которой действуют только консервативные силы, с течением времени не изменяется: Е=const.

Если на систему действуют помимо консервативных сил еще и неконсервативные силы, то:


Работа консервативных сил равна:

В этом случае изменение полной механической энергии системы равно работе неконсервативных сил:

Вывод: в системе, в которой кроме консервативных сил, действуют также неконсервативные силы, полная механическая энергия системы не сохраняется, и закон сохранения механической энергии не выполняется. Но всегда возникает эквивалентное количество энергии другого вида взамен механической энергии. Таким образом, выполняется фундаментальный закон сохранения и превращения энергии. Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.

+5