Слайд 2
Тема 2. ВОДОРОДОПОДОБНЫЕ СИСТЕМЫ
В КВАНТОВОЙ МЕХАНИКЕ
2.1.
Квантовомеханическая картина строения
атома
2.2. Квантовые числа
2.3. Пространственное квантование
(Магнитное квантовое число)
2.42.4.2.4.
Спин электрона. Опыт Штерна и Герлаха
х
Слайд 3
Дополнение механической планетарной модели Резерфорда квантовыми постулатами
Бора-Зоммерфельда -
Слайд 4
приводит к согласию с экспериментальными данными Ангстрема,
Бальмера, Зеемана и других исследователей.
Слайд 5
И все же ….
Теория Бора-Зоммерфельда использовала два принципиально
различных подхода:
Слайд 6
понятие непрерывной траектории механики Ньютона,
- представление о дискретных квантовых состояниях.
Слайд 7
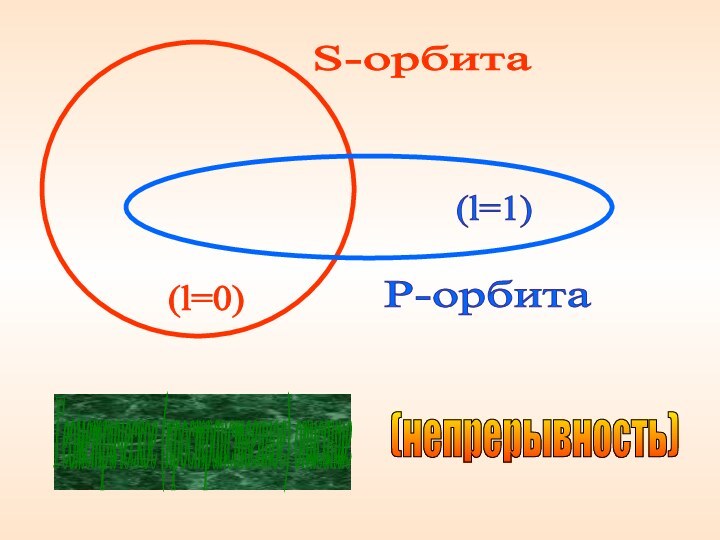
Геометрическое (пространственное) описание
(l=0)
(l=1)
S-орбита
P-орбита
(непрерывность)
Слайд 9
Аналогия теории Бора -
Зоммерфельда
как слияния двух описаний микромира
(Feline)
Слайд 10
Дальнейшее развитие квантовой механики привело к отказу от
механической картины движения электрона в поле ядра.
Слайд 11
Планетарная модель была заменена квантово-волновым описанием строения атома.
Слайд 12
2.1. Квантовомеханическая картина строения атома
х
На прошлой лекции мы
обсуждали ограниченность боровской теории строения атома. Рассмотрим теперь квантовомеханическую
теорию атомов, гораздо более полную, чем старая теория Бора. Она сохраняет некоторые аспекты старой теории.
Например, электроны могут находиться в атоме только в дискретных состояниях с определенной энергией; при переходе электрона из одного состояния в другое испускается (или поглощается) фотон. Но квантовая механика – не просто обобщение теории Бора.
Она представляет собой гораздо более глубокую теорию и рисует совершенно иную картину строения атома.
Слайд 13
Согласно квантовой механике, не существует определенных круговых орбит
электронов, как в теории Бора.
В силу волновой природы
электрон «размазан» в пространстве, подобно «облаку» отрицательного заряда.
Для основного состояния атома можно вычислить:
х
где Ψ(r) – волновая функция положения, зависящая от расстояния r до центра;
r1 - радиус первой боровской орбиты.
(1)
Слайд 14
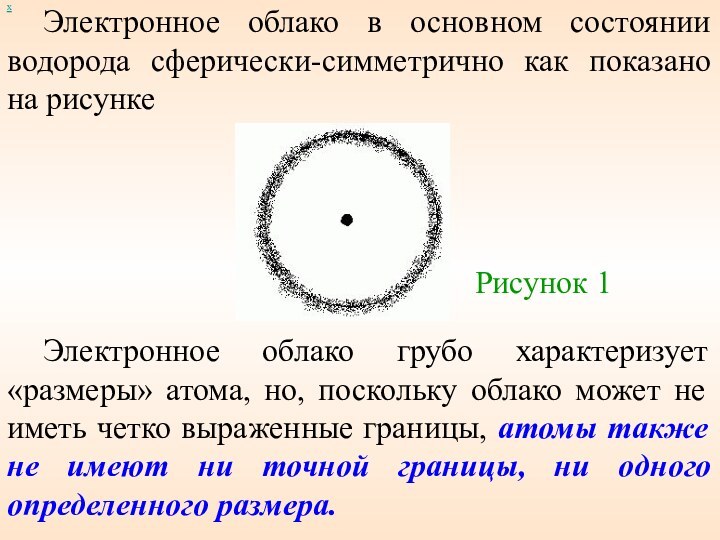
Электронное облако в основном состоянии водорода сферически-симметрично
как показано на рисунке
х
Электронное облако грубо характеризует «размеры»
атома, но, поскольку облако может не иметь четко выраженные границы, атомы также не имеют ни точной границы, ни одного определенного размера.
Рисунок 1
Слайд 15
х
Как мы увидим в дальнейшем, не все электронные
облака сферически-симметричны. Обратите внимание на то, что хотя функция
Ψ(r) при больших радиусах r, как следует из приведенного выше выражения сильно убывает, она не обращается в нуль на конечных расстояниях.
Квантовая механика утверждает, что основная часть атома не представляет собой пустое пространство.
Т.к. Ψ→0 только при r→∞, мы заключаем, что и во вселенной не существует в подлинном смысле пустого пространства.
Слайд 16
х
Электронное облако можно интерпретировать как с корпускулярной, так
и с волновой точки зрения.
Напомним, что под частицей
мы понимаем нечто локализованное в пространстве: в любой момент времени частица занимает вполне определенное положение в пространстве. Следовательно, размытое в пространстве облако является результатом волновой природы электронов.
Электронное облако можно также интерпретировать как распределение вероятностей для данной частицы.
Слайд 17
х
Если измерить положение электрона 1000 раз, то большинство
результатов измерений соответствовало бы точкам, в которых вероятность велика,
хотя электрон случайно может оказаться и там, где вероятность мала.
Мы не можем предсказать траектории, по которой будет двигаться электрон.
После измерения положения электрона точно предсказать, где будет находиться электрон в последующие моменты времени, невозможно.
Слайд 18
х
Мы можем лишь вычислить вероятность обнаружить электрон в
различных точках. Ясно, что подобная ситуация в корне отличается
от классической Ньютоновской физики. Как отмечал впоследствии Н.Бор, при испускании атомом светового фотона, бессмысленно даже спрашивать, как электрон переходит из одного состояния в другое.
Решение задачи об энергетических уровнях электрона для водорода (а также водородных систем: атома гелия He+, лития Li2+ и др.) сводится к задаче о движении электрона в кулоновском поле ядра.
Слайд 19
Потенциальная энергия взаимодействия электрона с ядром, обладающим
зарядом Ze (для атома водорода Z = 1)
х
где
r – расстояние между электроном и ядром.
(2)
Слайд 20
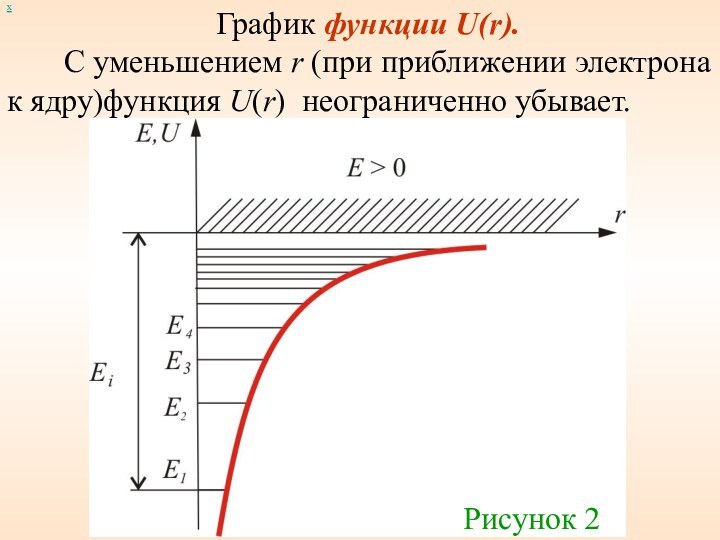
График функции U(r).
С
уменьшением r (при приближении электрона к ядру)функция U(r) неограниченно
убывает.
х
Рисунок 2
Слайд 21
х
Шредингер Эрвин (1887 – 1961) – австрийский физик-теоретик,
один из создателей квантовой механики. Основные работы в области
статистической физики, квантовой теории, квантовой механики, общей
теории относительности, биофизики. Разработал теорию движения микрочастиц – волновую механику, построил квантовую теорию возмущений – приближенный метод в квантовой механике. За создание волновой механики удостоен Нобелевской премии.
Слайд 22
Состояние электрона в атоме водорода описывается волновой
функцией Ψ, удовлетворяющей стационарному уравнению Шредингера:
х
E – полная энергия
электрона в атоме.
- потенциальная энергия
Уравнения типа (3) имеют решение, удовлетворяющее однозначности, конечности и непрерывности волновой функции Ψ, только при собственных значениях энергии:
(3)
где n = 1, 2, 3,…, т.е. дискретного набора отрицательных значений энергии.
Слайд 23
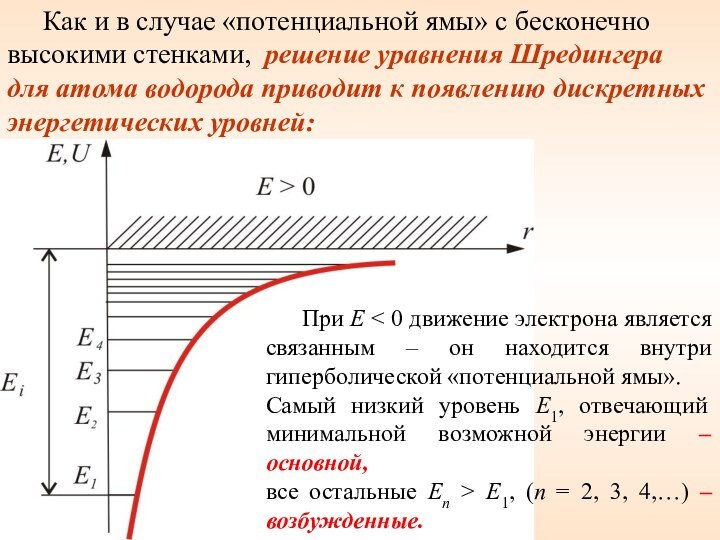
Как и в случае «потенциальной ямы» с бесконечно
высокими стенками, решение уравнения Шредингера для атома водорода приводит
к появлению дискретных энергетических уровней:
При E < 0 движение электрона является связанным – он находится внутри гиперболической «потенциальной ямы». Самый низкий уровень E1, отвечающий минимальной возможной энергии – основной,
все остальные En > E1, (n = 2, 3, 4,…) – возбужденные.
Слайд 24
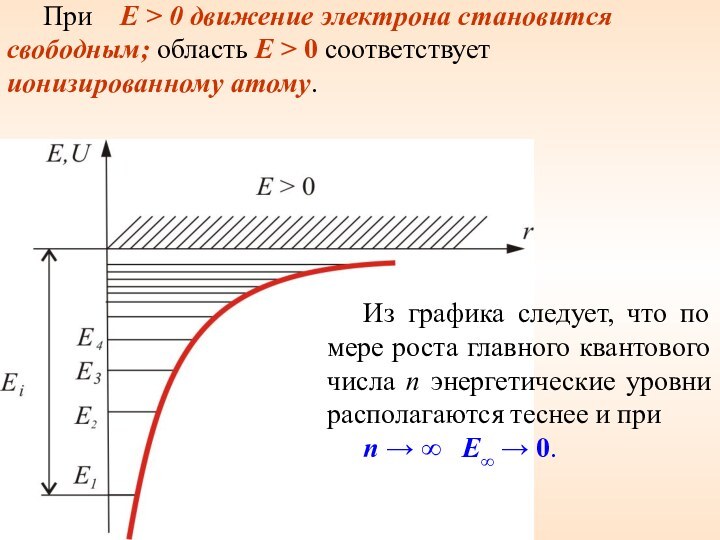
При E > 0 движение электрона становится
свободным; область E > 0 соответствует ионизированному атому.
Из графика
следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при
n → ∞ E∞ → 0.
Слайд 25
Итак, если Бору пришлось вводить дополнительные гипотезы (постулаты),
то в квантовой механике дискретные значения энергии, являясь следствием
самой теории, вытекают непосредственно из решения уравнения Шредингера:
Слайд 26
В квантовой механике доказывается, что уравнению Шредингера удовлетворяют
собственные функции
, определяемые тремя квантовыми числами:
главным n,
орбитальным l
магнитным m.
Как уже сказано в предыдущих параграфах – главное квантовое число n, определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с единицы (n = 1, 2, 3,…).
х
2.2. Квантовые числа
Слайд 27
Главное квантовое число n характеризует расстояние электрона
от ядра – радиус орбиты.
х
В атомной
физике состояния электрона, соответствующие главному квантовому числу n,
(n = 1, 2, 3, 4,…) принято обозначать буквами K, L, M, N,….
Слайд 28
Состояния, соответствующие орбитальному числу l = 0, 1,
2, 3,…, также обозначаются буквами
s, p, d,
f,….
Орбитальное квантовое число
l = 0, 1, 2,...n – 1
характеризует эллиптичность орбиты электрона и определяет момент импульса электрона L
sharp, principal,
diffuse, fundamental
Слайд 29
Эллиптические орбиты А. Зоммерфельда
1915 г.
Слайд 30
Квадрат модуля функции
характеризует вероятность найти электрон
в заданной точке. Область пространства,
в которой высока вероятность обнаружить электрон (не менее 0,95), называют орбиталью.
Слайд 31
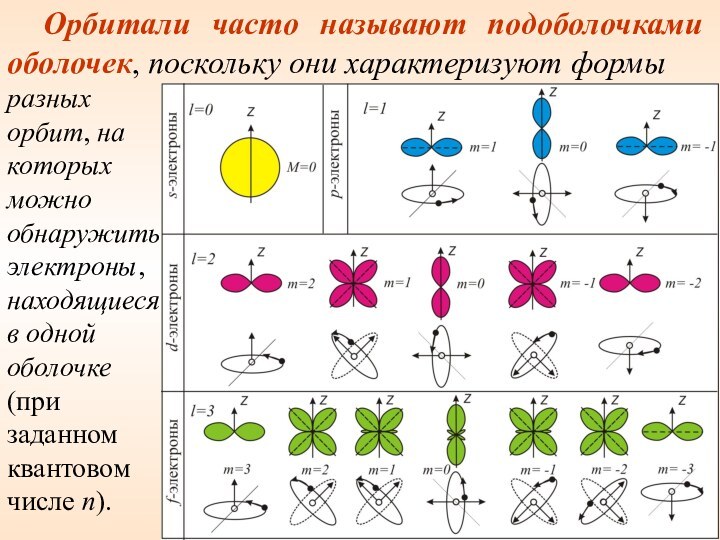
Орбитали часто называют подоболочками оболочек, поскольку они характеризуют
формы
разных орбит, на которых можно обнаружить электроны, находящиеся в
одной оболочке (при заданном квантовом числе n).
Слайд 32
х
Решая последовательно задачу об электроне в прямоугольной потенциальной
яме мы доказали только то, что энергия и положение
электрона квантуются, т.е. принимают дискретные значения.
Решая уравнения Шредингера для атома можно получить выражения для энергии, момента импульса и других динамических переменных электрона без привлечения каких-либо постулатов.
Слайд 33
Рассмотрим (без вывода) движение
электрона в потенциальном поле
Стационарное
уравнение Шредингера
х
(1)
Так как электрическое поле – центрально-симметрично, то для решения этого уравнения воспользуемся сферической системой координат: r, θ, φ.
Слайд 34
Воспользуемся сферической системой с координатами (r, θ, φ),
которые связаны с декартовыми координатами, как это следует из
рисунка, соотношениями:
;
;
.
Слайд 35
Подставим в (1) выражение оператора Лапласа
в сферических координатах, получим уравнение Шредингера в виде:
х
(2)
Уравнение (2) имеет решение при всех значениях E > 0, это соответствует свободному электрону: При Е < 0
где n = 1, 2, 3…,
т.е. энергия принимает
дискретные значения.
Вывод такой же как и в теории Бора, но здесь этот вывод получается как естественное следствие из уравнения Шредингера.
Слайд 36
В квантовой механике широко используется понятие –
оператор. Под оператором понимают правило, посредством которого одной функции
φ сопоставляется другая функция f т е.
х
– символ обозначения оператора.
Есть операторы импульса, момента импульса и т.д.
– оператор скорости;
– ускорения.
Если S – путь, то
– скорость и т.д.
Слайд 37
х
С помощью оператора стационарное уравнение Шредингера можно записать
в виде
(4)
Здесь
– оператор энергии.
Это традиционный вид записи уравнения
Шредингера.
Слайд 38
х
Для момента импульса в
квантовой механике вводятся четыре оператора: оператор квадрата
момента импульса
и
три оператора проекций
момента импульса на оси координат
Воздействуя на Ψ – функцию, полученную при решении уравнения (2) оператором момента импульса (движение электрона вокруг ядра осуществляется по криволинейной траектории) можно получить выражение для момента импульса.
Слайд 39
х
Решение этого уравнения является очень трудным
Ограничимся
только конечным результатом:
Собственное значение орбитального момента импульса электрона
Le
(5)
l – орбитальное квантовое число(l = 0, 1, 2,… n – 1) Из этого выражения видно, что момент импульса электрона в атоме тоже квантуется.
Уравнение для момента
импульса электрона.
Слайд 40
х
Если обратиться к привычной нам модели атома, то:
n – характеризует среднее расстояние электрона
от ядра (радиус орбиты);
l – характеризует эллиптичность орбиты:
Слайд 41
Основным состоянием электрона в атоме водорода является s
– состояние:
Слайд 42
х
Если вычислить наиболее вероятное расстояние
от ядра для электрона
в s –состоянии, получим:
– это первый Боровский радиус
в СИ:
Для других значений n получим выражения, соответствующие следующим Боровским орбитам.
Слайд 43
х
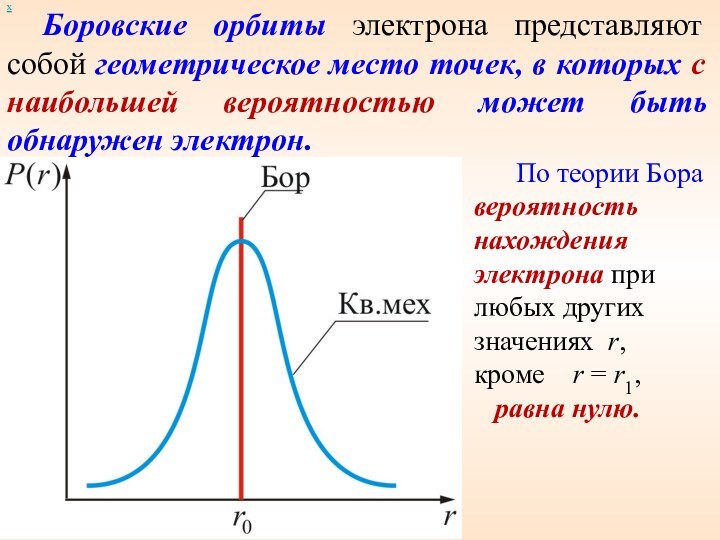
Боровские орбиты электрона представляют собой геометрическое место точек,
в которых с наибольшей вероятностью может быть обнаружен электрон.
По теории Бора вероятность нахождения электрона при любых других значениях r,
кроме r = r1,
равна нулю.
Слайд 44
х
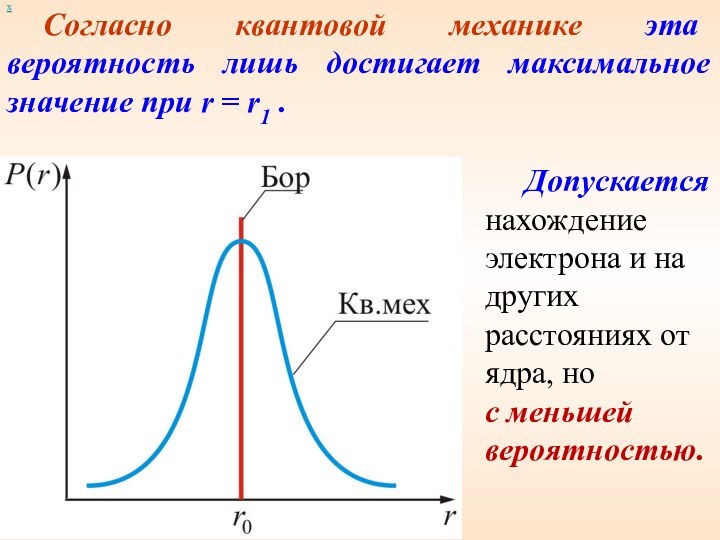
Согласно квантовой механике эта вероятность лишь достигает максимальное
значение при r = r1 .
Допускается
нахождение электрона и на других расстояниях от ядра, но
с меньшей вероятностью.
Слайд 46
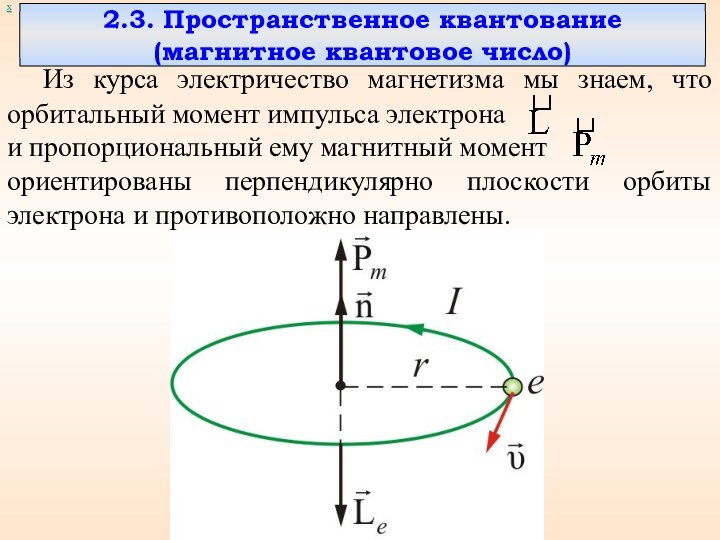
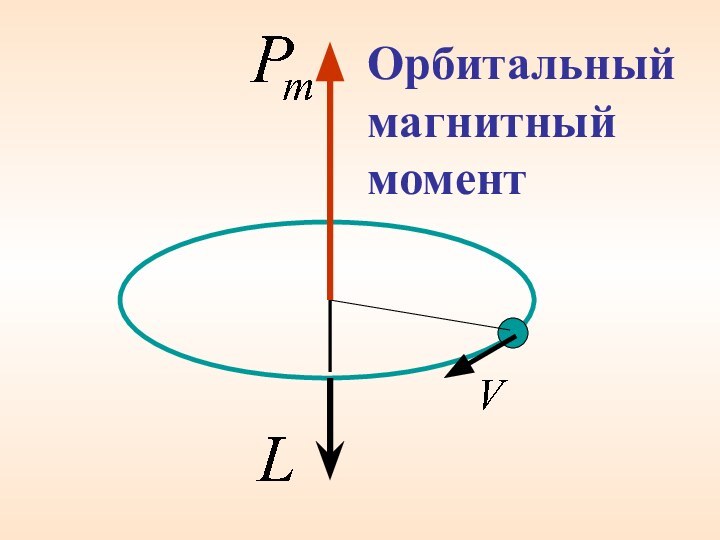
Из курса электричество магнетизма мы знаем, что
орбитальный момент импульса электрона
и пропорциональный
ему магнитный момент
ориентированы перпендикулярно плоскости орбиты электрона и противоположно направлены.
х
2.3. Пространственное квантование
(магнитное квантовое число)
Слайд 47
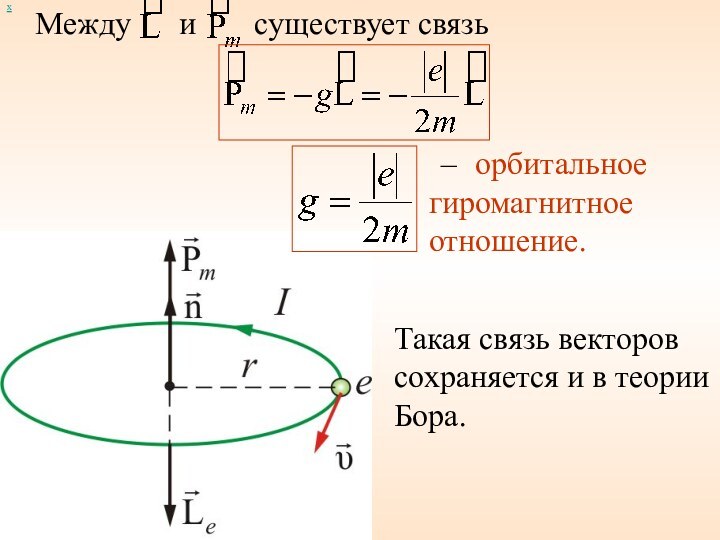
Между и
х
существует связь
– орбитальное
гиромагнитное отношение.
Такая связь векторов сохраняется
и в теории Бора.
Слайд 48
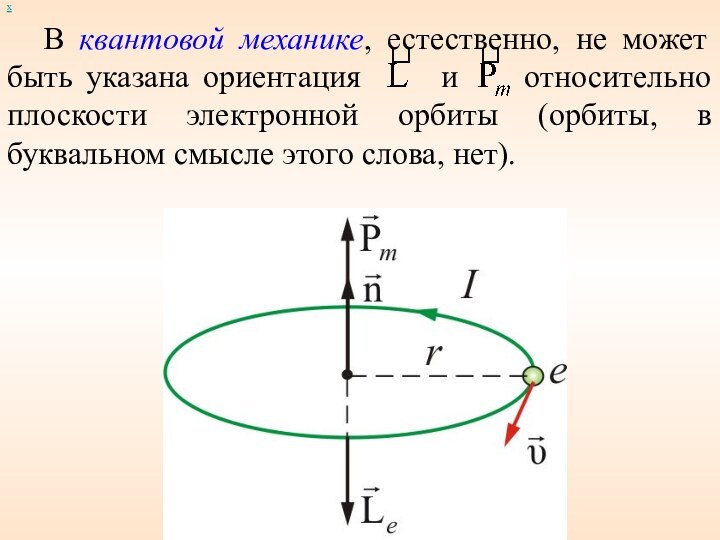
В квантовой механике, естественно, не может быть указана
ориентация и относительно плоскости электронной
орбиты (орбиты, в буквальном смысле этого слова, нет).
х
Слайд 49
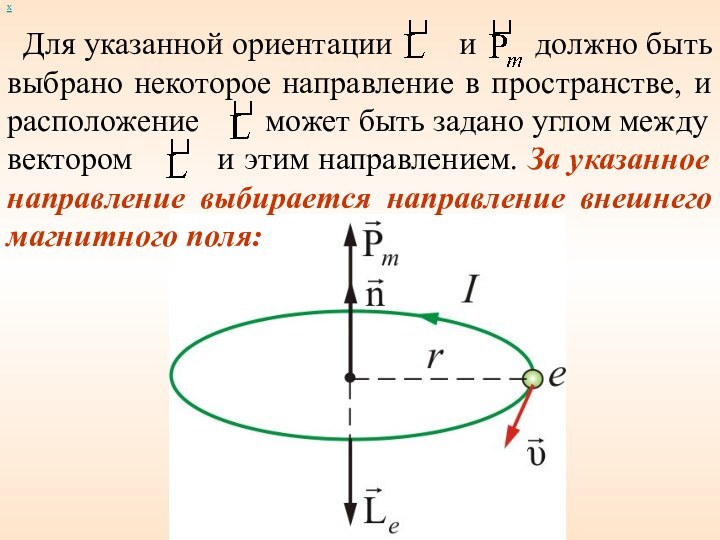
Для указанной ориентации и
должно быть выбрано некоторое направление в
пространстве, и расположение может быть задано углом между вектором и этим направлением. За указанное направление выбирается направление внешнего магнитного поля:
х
Слайд 50
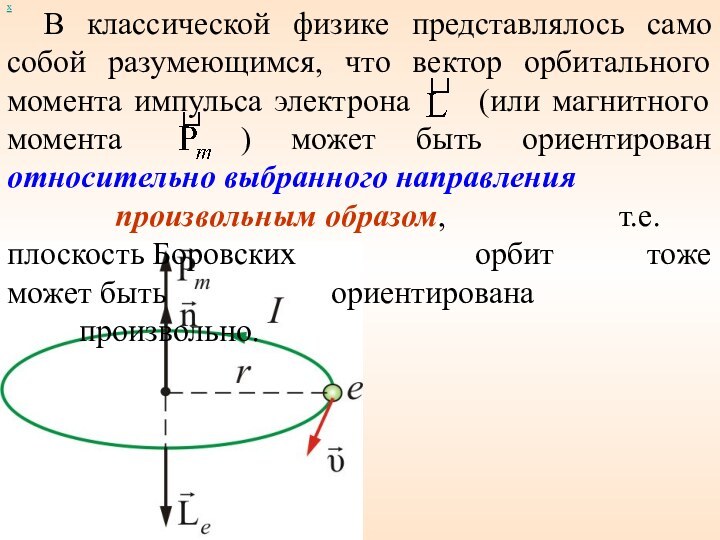
В классической физике представлялось само собой разумеющимся, что
вектор орбитального момента импульса электрона (или магнитного
момента ) может быть ориентирован относительно выбранного направления произвольным образом, т.е. плоскость Боровских орбит тоже может быть ориентирована произвольно.
х
Слайд 51
Однако, такое предположение оказалось ошибочным.
В квантовой механике
строго доказывается (это следует из решения уравнения Шредингера), что
проекция (Lz) вектора на направление внешнего поля (z) может принимать лишь целочисленные значения кратные ħ
х
(2.3.2)
m = 0, ±1, ±2,…±l – магнитное квантовое число.
l – орбитальное квантовое число,
Таким образом, может принимать (2l + 1)
ориентаций в пространстве.
Слайд 52
Определим величину модуля .
Т.к.
проекция не может быть больше модуля вектора, то, следовательно
. Отсюда следует, что максимальное значение |m| = l (m – целое число).
Итак, m тоже может принимать (2l + 1) значений (l = 0 дает одно «лишнее» значение),
т. е. может принимать (2l + 1) ориентаций в пространстве.
х
Слайд 53
х
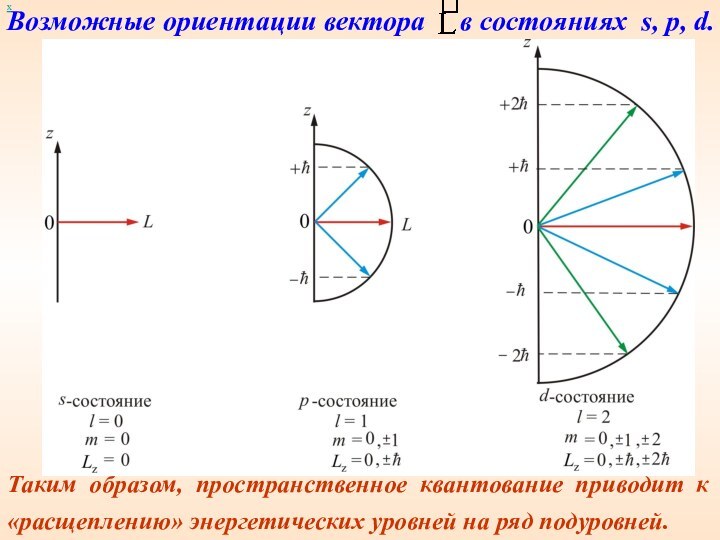
Таким образом, пространственное квантование приводит к «расщеплению» энергетических
уровней на ряд подуровней.
Возможные ориентации вектора
в состояниях s, p, d.
Слайд 54
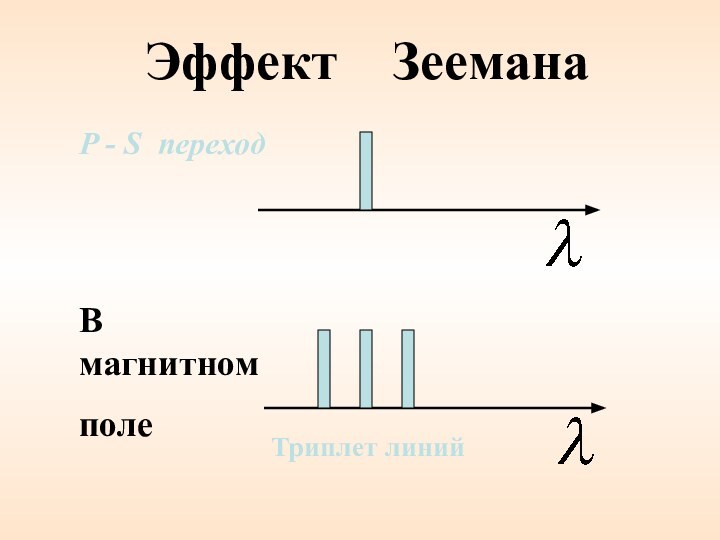
Расщепление энергетических уровней в
магнитном поле было обнаружено в 1896 г. голландским физиком
П. Зееманом и получило название эффекта Зеемана.
Расщепление уровней энергии во внешнем электрическом поле тоже доказано экспериментально и называется эффектом Штарка.
Слайд 55
Эффект Зеемана
В магнитном
поле
P - S переход
Триплет линий
Слайд 57
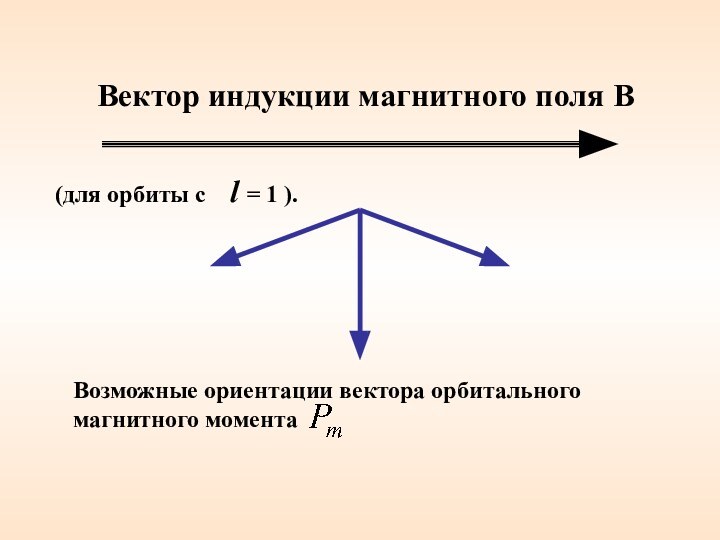
Вектор индукции магнитного поля В
Возможные ориентации вектора орбитального
магнитного момента
(для орбиты с l = 1
).
Слайд 58
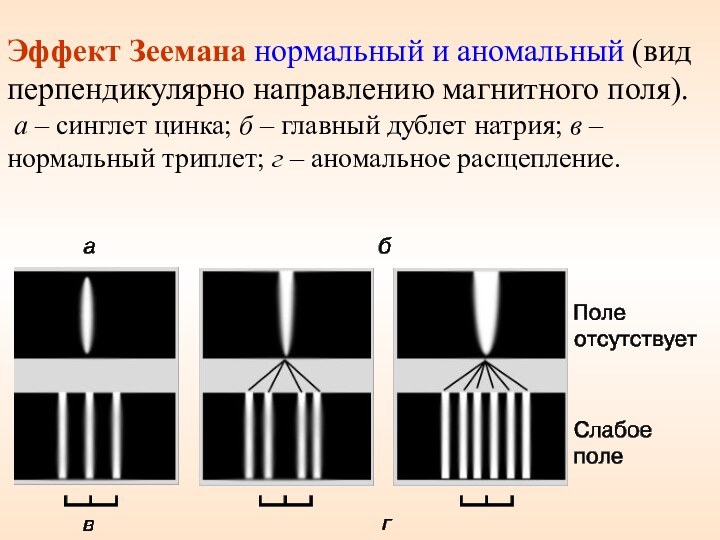
Эффект Зеемана нормальный и аномальный (вид перпендикулярно направлению
магнитного поля).
а – синглет цинка; б – главный
дублет натрия; в – нормальный триплет; г – аномальное расщепление.
Слайд 59
х
2.4. Опыт Штерна и Герлаха.
В 1922 году
Штерн и Герлах поставили опыты, целью которых было измерение
магнитных моментов Pm атомов различных химических элементов.
Для химических элементов, образующих первую группу таблицы Менделеева и имеющих один валентный электрон, магнитный момент атома равен магнитному моменту валентного электрона, т. е. одного электрона.
Слайд 60
х
Идея опыта заключалась в измерении силы, действующей на
атом в сильно - неоднородном магнитном поле.
Неоднородность магнитного
поля должна быть такова, чтобы она сказывалась на расстояниях порядка размера атома. Только при этом можно было получить силу, действующую на каждый атом в отдельности.
Слайд 61
х
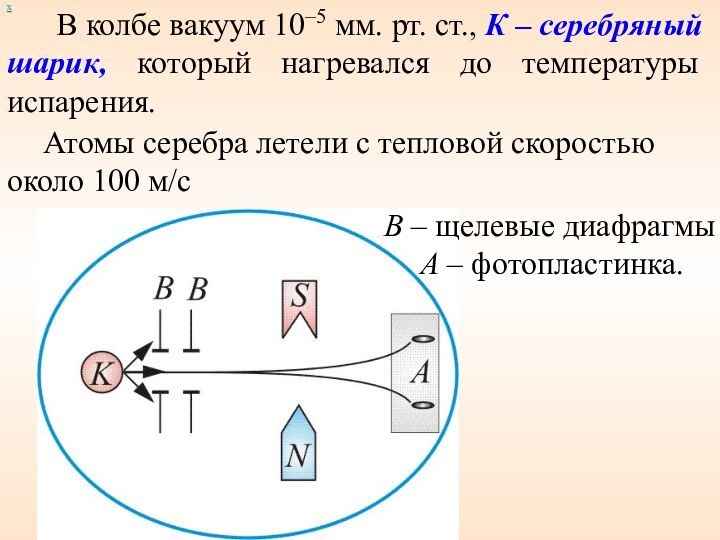
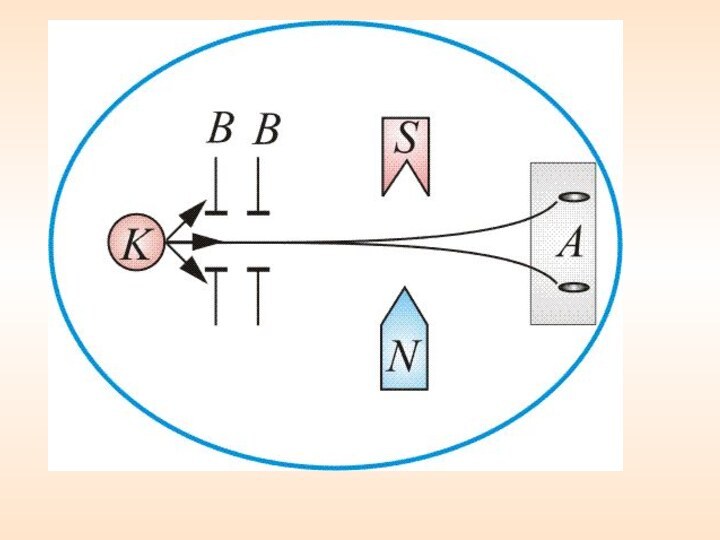
В колбе вакуум 10–5 мм.
рт. ст., К – серебряный шарик, который нагревался до
температуры испарения.
Рисунок 5
Атомы серебра летели с тепловой скоростью около 100 м/с
В – щелевые диафрагмы А – фотопластинка.
Слайд 62
х
Если бы момент импульса атома
(и его магнитный момент ) мог принимать произвольные
ориентации в пространстве, т.е. в магнитном поле, то можно было ожидать непрерывного распределения попаданий атомов серебра на фотопластинку с большой плотностью попаданий в середине.
Но на опыте были получены совершенно неожиданные результаты: на фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояким образом, соответствующим лишь двум возможным ориентациям магнитного момента (рисунок 6).
Слайд 65
Этим доказывался квантовый характер магнитных моментов электронов.
Количественный
анализ показал, что проекция магнитного момента электрона равна
х
– магнетон Бора
Т.е. для серебра Штерн и Герлах получили, что проекция магнитного момента атома (электрона) на направление магнитного поля численно равна магнетону Бора.
Напомню:
Слайд 66
х
Опыты Штерна и Герлаха не только подтвердили пространственное
квантование моментов импульсов в магнитном поле, но и дали
экспериментальное подтверждение тому, что магнитные моменты электронов тоже состоят из некоторого числа «элементарных моментов», т.е. имеют дискретную природу.
Единицей измерения магнитных моментов электронов и атомов является магнетон Бора
(ħ – единица измерения механического момента импульса).
Слайд 67
х
Кроме того, в этих опытах было обнаружено новое
явление. Валентный электрон в основном состоянии атома серебра имеет
орбитальное квантовое число l = 0 (s – состояние).
Но при l = 0,
(проекция момента импульса на направление внешнего поля равна нулю).
Возник вопрос, пространственное квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна магнетону Бора?
Слайд 68
х
В 1925 г. студенты Геттингенского университета Гаудсмит и
Уленбек предложили существование собственного механического момента импульса у электрона
S (спина) и, соответственно, собственного магнитного момента электрона mS.
Введение понятия спина сразу объяснило ряд затруднений, имевшихся к тому времени в квантовой механике и в первую очередь, результатов опытов Штерна и Герлаха.
Слайд 69
Спин электрона S
Собственный магнитный момент электрона
Слайд 70
х
Спин, как заряд и масса
есть свойство электрона
П.Дирак впоследствии показал, что
существование спина вытекает из решения релятивистского волнового уравнения Шредингера.
Из общих выводов квантовой механики следует, что спин
S –спиновое квантовое число.
Авторы дали такое толкование спина: электрон вращающийся волчок.
Но тогда следует, что «поверхность» волчка (электрона) должна вращаться с линейной скоростью равной 300с, где с – скорость света.
От такого толкования спина пришлось отказаться.
Слайд 71
х
Аналогично, проекция спина на ось z (LSz) (ось
z совпадает с направлением внешнего магнитного поля) должна быть
квантована и вектор LSz может иметь (2S + 1) различных ориентаций в магнитном поле.
Из опытов Штерна и Герлаха следует, что таких ориентаций всего две:
2S + 1 = 2,
а значит S = 1/2.
Слайд 72
х
Для атомов первой группы, валентный электрон которых находится
в s – состоянии (l = 0) момент импульса
атома равен спину валентного электрона.
Поэтому обнаруженное для таких атомов пространственное квантование момента импульса в магнитном поле является доказательством наличия у спина лишь двух ориентаций во внешнем поле.
(Опыты с электронами в p – состоянии подтвердили этот вывод, хотя картина получилась более сложной) (желтая линия натрия – дуплет из-за наличия спина).
Слайд 73
х
Численное значение спина электрона
По
аналогии с пространственным квантованием орбитального момента (L) проекция LSz
= mSħ,
т.е. тоже должна быть квантованной величиной (аналогично, как m = ± e, то и mS = ±S).
Проекция спина на направление внешнего магнитного поля, являясь квантовой величиной, определяется выражением:
где – магнитное спиновое квантовое число.
может принимать только два значения, что и наблюдается в опыте Штерна и Герлаха.
Слайд 74
И так магнитное спиновое квантовое число
может
принимать два значения.
Спиновое квантовое число S имеет только одно
значение S = 1/2.
Итак, проекция спинового механического момента импульса на направление внешнего магнитного поля может принимать два значения:
х
(2.4.1)
Так как мы всегда имеем дело с проекциями, то говоря, что спин имеет две ориентации; имеем в виду, что две проекции.
Слайд 75
Проекция магнитного момента электрона на направление внешнего поля:
(часто
говорят о собственном магнитном моменте электрона)
Отношение
– спиновое
гиромагнитное отношение.