- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Выбор алгоритма классификации для дистанционного зондирования Земли. Характеристики данных Landsat 8
Содержание
- 2. Для распределения пикселов снимка по классам можно
- 3. Алгоритм классификации на основе определения наименьшего расстоянияЭтот
- 4. Алгоритм параллелепипедаЭтот алгоритм классификации основан на обычной
- 5. Множество точек, подчиняющихся этому условию, образует параллелепипед
- 6. Алгоритм максимального правдоподобияВ рассмотренных методах классификации не
- 7. Если нет дополнительных сведений о пространственных объектах,
- 8. Методы неконтролируемой классификацииПри использовании методов неконтролируемой классификации
- 9. Этап 1. Выделение кластеровДля выполнения этого этапа
- 10. Этап 2. Классификация пикселов снимкаПосле выделения центров
- 11. Оценка точности классификацииКлассификацию данных дистанционного зондирования нельзя
- 12. Матрица ошибокСтандартной формой представления оценки точности классификации
- 14. Запущен весной 1984 .Прекратил работу осенью 2011.Характеристики снимков Landsat 5 TM
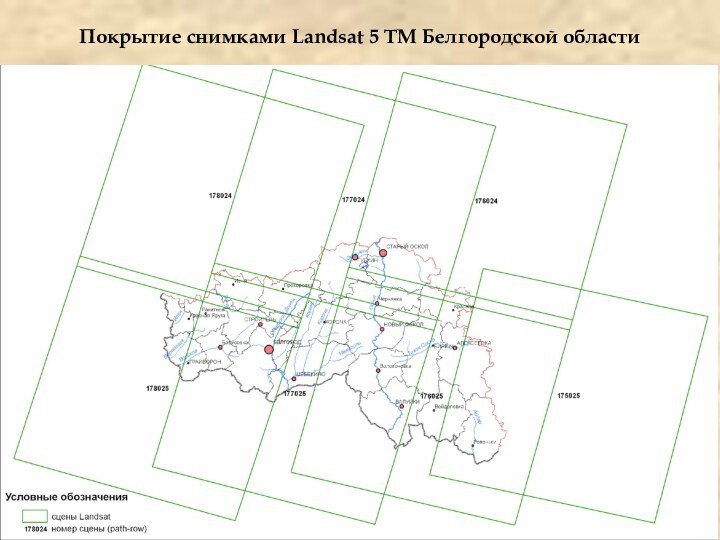
- 16. Покрытие снимками Landsat 5 TM Белгородской области
- 17. Характеристики данных Landsat 8Запущен в феврале 2013 .Доступен для скачивания с конца мая 2013
- 18. Дешифрование гарей разного возраста22 апреля 20116 мая
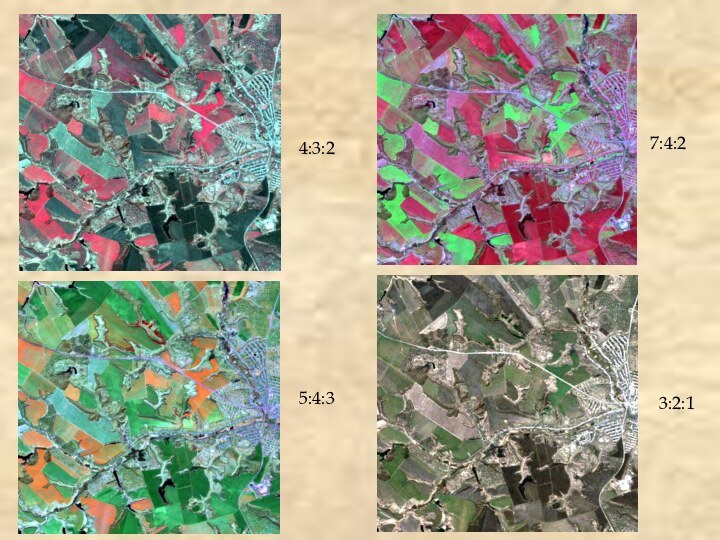
- 19. 4:3:25:4:37:4:23:2:1
- 20. Дешифрование пламениВ комбинации каналов Landsat 7:5:3 пламя
- 21. 16 апреля 1994 года. Видно 26 очагов
- 22. Дешифрование дымаДым лучше всего виден в комбинации
- 23. Травяные палы на западе Белгородской области22 апреля
- 24. Палы на территории ООПТ6 мая 2007На снимке
- 25. Весенние травяные палы в региональном природном парке
- 26. Скачать презентацию
- 27. Похожие презентации
Для распределения пикселов снимка по классам можно использовать разные методы, причем выбор того или иного классифицирующего правила зависит от типа исходных данных и решаемой задачи. Все методы классификации можно разделить на параметрические и непараметрические. При использовании


















Слайд 3
Алгоритм классификации на основе определения наименьшего расстояния
Этот алгоритм
является одним из самых простых и наиболее часто используемых.
Входными данными служат средние векторы, полученные на этапе обучения для каждого класса и каждого спектрального диапазона. Для каждого значения яркости пиксела (BV#), не относящегося к обучающей выборке, вычисляется эвклидово расстояние D до среднего вектора цс(к в соответствии с формулой:Пиксел приписывается тому классу, для которого это расстояние оказывается наименьшим. Интересно отметить, что точность классификации этим методом сравнима с той точностью, которую обеспечивают более сложные вычислительные алгоритмы, в частности алгоритм максимального правдоподобия.
Слайд 4
Алгоритм параллелепипеда
Этот алгоритм классификации основан на обычной булевой
логике и статистических показателях обучающей выборки в п спектральных
диапазонах. Сначала для каждого класса с и диапазона к вычисляется среднее значение яркости в обучающей выборке и аск.После этого для классификации пикселов снимка применяют следующее правило. Пиксел принадлежит классу с тогда и только тогда, когда его яркость ВУ/Д удовлетворяет следующему условию:
где с = 1,2, 3, ... т обозначает класс, а к = 1,2, 3, ... т — спектральный диапазон.
Если обозначить нижнюю и верхнюю границу этого неравенства как
Слайд 5 Множество точек, подчиняющихся этому условию, образует параллелепипед в
n-мерном пространстве спектральных признаков. Если значения яркости пиксела лежат
внутри этого параллелепипеда, пиксел приписывается данному классу. В противном случае пиксел относят к категории неклассифицируемых.
Слайд 6
Алгоритм максимального правдоподобия
В рассмотренных методах классификации не учитывались
возможные вариации спектральных признаков и проблемы, возникающие из-за пересечения
классов. Последние часто возникают в тех случаях, когда требуется классифицировать пикселы, близкие по своим спектральным характеристикам.В методе максимального правдоподобия пиксел приписывается к тому классу, который максимизирует функцию правдоподобия классификации. Данные из обучающей выборки используются для вычисления среднего вектора измерений Мс и ковариационной матрицы Vc для каждого класса с и спектрального диапазона к.
Критерий принадлежности пиксела к определенному классу формулируется следующим образом. Пиксел х принадлежит классу с в том и только в том случае, если
Слайд 7 Если нет дополнительных сведений о пространственных объектах, вероятность
р для всех классов будет одинаковой. Если же известно,
что вероятность существования одних классов больше, чем других, оператор может задать набор априорных значений вероятности для соответствующих спектральных признаков. Критерий принадлежности пиксела к определенному классу, при этом, будет формулироваться следующим образом.Пиксел х принадлежит классу с в том и только в том случае, если
Использование априорных вероятностей позволяет учитывать особенности рельефа и других характеристик территории. В то же время, к недостаткам алгоритма максимального правдоподобия следует отнести то, что для расчетов этим методом требуются большой объем памяти и значительное время, при этом результаты классификации часто оказываются не самым лучшим.
Слайд 8
Методы неконтролируемой классификации
При использовании методов неконтролируемой классификации от
оператора практически не требуется вводить каких-либо входных данных. Все
операции выполняются автоматически, при этом программа анализирует пространство спектральных параметров и на основании определенных критериев разделяет пикселы на классы, рассчитывая для каждого из них средние значения признаков и ковариационные матрицы. После того как все данные распределены по спектральным классам, оператор старается сопоставить их с известными информационными классами пространственных объектов. Эта задача зачастую оказывается весьма непростой. Некоторые спектральные классы (кластеры) могут не соответствовать каким-либо классам пространственных объектов или соответствовать сразу нескольким из них. Указанная неоднозначность может быть устранена только оператором на основе дополнительной информации о спектральных характеристиках изучаемых объектов. Алгоритмы кластерного анализа, применяемые для неконтролируемой классификации данных ДЗ, различаются, прежде всего, своей эффективностью. Для того чтобы пояснить основные принципы кластерного анализа, рассмотрим пример очень простого, хотя и не всегда эффективного, алгоритма, который называется CLUSTER.Алгоритм реализован в виде двух последовательных этапов: на первом этапе выделяются кластеры, а на втором каждый пиксел данных относится к тому или иному кластеру (классу) в соответствии с критерием минимального расстояния. Рассмотрим каждый из этапов этого алгоритма более подробно.
Слайд 9
Этап 1. Выделение кластеров
Для выполнения этого этапа от
оператора могут потребоваться следующие данные:
Процесс анализа начинается с того,
что в качестве центра первого кластера выбирается первый пиксел снимка. Затем в пространстве спектральных признаков вычисляется расстояние между этой точкой и вторым пикселом. Если это расстояние меньше или равно R, пиксел присваивается классу 1, а новый центр класса определяют, рассчитывая среднее значение по двум пикселам. Если же расстояние между пикселами больше R, тот новый пиксел становится центром класса 2. После этого все перечисленные действия повторяются для всех пикселов вплоть до N, при этом проверяется их принадлежность ко всем ранее выделенным классам.Следующий шаг состоит в проверке разделимости выделенных классов. На этом этапе рассматриваются расстояния между центрами классов, которые не должны быть меньше заданного значения С. Если расстояние между двумя центрами кластеров меньше С, они объединяются, а центр нового кластера вычисляется как взвешенное среднее центров исходных кластеров. После проверки разделимости процесс выделения кластеров возобновляется. Интересно заметить, что в дальнейшем центры кластеров стремятся вернуться в свои исходные положения. Процесс построения кластеров продолжается до тех пор, пока не будет достигнуто максимально допустимое количество кластеров (Стах) или пока не будет проанализирован последний пиксел снимка. В заключение еще раз выполняется проверка разделимости кластеров.
Слайд 10
Этап 2. Классификация пикселов снимка
После выделения центров кластеров
каждый пиксел снимка присваивается одному из выделенных классов в
соответствии с критерием минимального расстояния. Затем наступает очередь оператора. Поскольку выделение кластеров и классификация пикселов выполнялись в пространстве спектральных признаков, оператор должен сопоставить спектральные классы информационным. Однако может оказаться, что для получения одного информационного класса необходимо объединить два или даже более спектральных классов. При этом размер результирующего кластера может оказаться слишком большим и потребуется разделить этот кластер на два. К сожалению, в алгоритме CLUSTER предусмотрена возможность объединения кластеров, но не их разделения.Обе эти возможности присутствуют в другом алгоритме, который называется ISODATA (Iterative self Organizing Data Analysis Technique А). Еще одной особенностью этого алгоритма является то, что в нем операции выделения центров кластеров и классификации пикселов изображения не разделены на два этапа, а выполняются одновременно. Недостатком этого алгоритма является то, что для его использования требуются большие вычислительные ресурсы и очень высокая квалификация оператора. Подробное описание этого алгоритма приведено в работе Харалика и Фу. Помимо перечисленных используют также ряд других алгоритмов классификации, в частности АМЕОВА и FORGY.
Слайд 11
Оценка точности классификации
Классификацию данных дистанционного зондирования нельзя считать
завершенной, пока не получена оценка ее точности. Оператор должен
определить, насколько точно классы объектов на снимке соответствуют классам объектов на земной поверхности. В области обработки изображений термин точность означает меру согласованности стандартной информации в некоторой пространственной точке с информацией в соответствующей точке классифицированного снимка. Обычно проверка точности классификации основана на сравнении двух карт — той, которая получена в результате анализа данных ДЗ, и второй, контрольной карты. Для построения контрольной карты обычно используют несколько источников данных, поэтому она считается более точной. Обычно на контрольной карте нанесено несколько отдельных участков земной поверхности, для каждого из которых используется отдельное условное обозначение.Простейшим методом определения точности классификации является сравнение тех участков двух карт, которые относятся к выделенным классам объектов. Результатом является отчет, в котором указывается общая точность классификации для всей карты или точность классификации отдельных ее участков.
Оценку общей точности классификации формулируют в единицах площади объектов каждого класса, не обращая внимания на несовпадение объектов в отдельных точках сравниваемых карт. При оценке точности классификации определенного участка карты расхождение между классами объектов анализируется более подробно.
При использовании метода контролируемой классификации, наиболее простой способ оценки ее точности состоит в сравнении классифицированных данных с обучающей выборкой. Однако этот способ приводит к завышенным оценкам точности. Строго говоря, если предположить, что обучающие выборки были сформированы безошибочно, то результирующая точность должна составлять 100%. По этой причине, гораздо более надежный способ оценки точности классификации заключается в том, чтобы выбрать данные, относящиеся к известному объекту, разделить эти данные на две части, а затем использовать одну из них в качестве обучающей выборки, а вторую — для оценки точности классификации.
Слайд 12
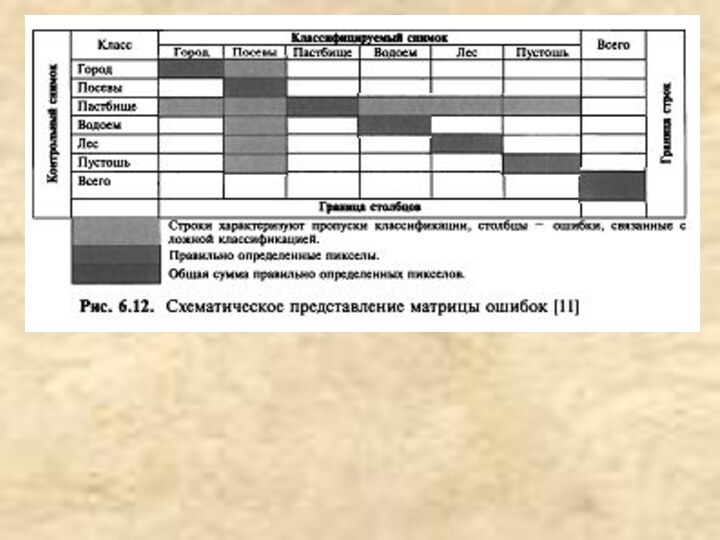
Матрица ошибок
Стандартной формой представления оценки точности классификации для
определенного местоположения является матрица ошибок, которая характеризует не только
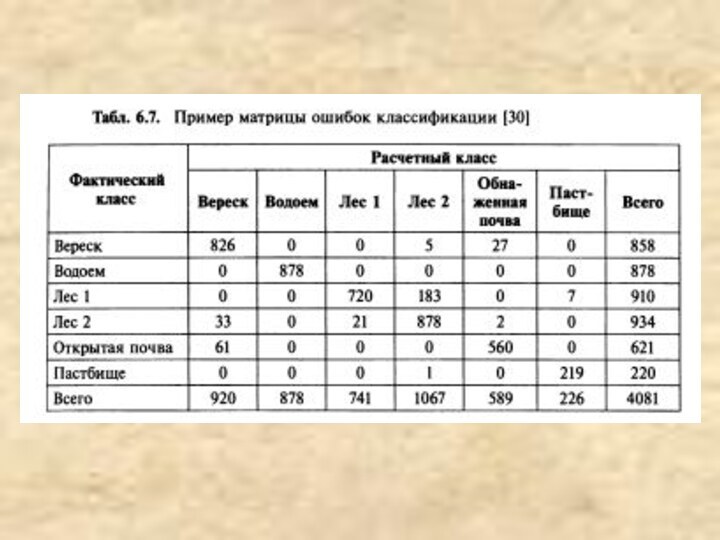
погрешность классификации для каждого класса, но и ошибки, связанные с неверной классификацией. Матрица ошибок состоит из я столбцов и л строк, где я — количество классов объектов на контрольной карте. Строки матрицы — это истинные классы, представленные на контрольной карте, а столбцы — классы, выделенные на анализируемой карте. Схематичное представление матрицы ошибок показано на рис. 6.12, а пример действительной матрицы приведен в табл. 6.7. В последнем столбце представлено количество точек в каждом информационном классе контрольной карты, а в последней строке матрицы — количество точек соответствующих классов на анализируемой карте. Диагональные элементы матрицы — это количество точек, принадлежащих одинаковым классам на обеих картах. Значение в нижнем правом углу таблицы представляет собой сумму диагональных элементов, то есть общее количество правильно классифицированных пикселов. Информация о ложной классификации или пропусках классификации содержится в недиагональных элементах матрицы.В табл. 6.7 для оценки точности классификации использовали данные, принадлежащие пяти информационным классам. Из 4421-го пиксела 4081 были идентифицированы правильно. Таким образом, общая точность классификации 0?') составила 92,3%. В предположении биномиального распределения для этой оценки можно сформулировать односторонний критерий значимости с помощью следующей формулы:
Слайд 17
Характеристики данных Landsat 8
Запущен в феврале 2013 .
Доступен
для скачивания с конца мая 2013
Слайд 18
Дешифрование гарей разного возраста
22 апреля 2011
6 мая 2007
1
– свежие, 2 – среднего возраста, 3 –старые, 4
– невыгоревшие участки Свежие гари имеют темно-бордовый (или вишневый) или темно-коричневый цвет. По мере зарастания травой он сменяется на бурый и палевый, а затем – на желтовато-зеленый. Постепенно цвет гарей и нетронутых огнем участков выравнивается, и к лету они уже неразличимы.
1
1
4
4
3
2
2
Слайд 20
Дешифрование пламени
В комбинации каналов Landsat 7:5:3 пламя выглядит
как небольшой по площади объект, площадью от нескольких до
нескольких десятков пикселей. Для него характерно сочетание ярко-желтого, оранжевого и красного цвета.пламя
пламя
пламя
1
2
3
1,2 – крупные очаги пламени на склонах балок; 3 – мелкие очаги пламени в населенном пункте
Слайд 21
16 апреля 1994 года. Видно 26 очагов пламени.
Дешифрование
пламени
1 – пожар у взлетной полосы белгородского аэропорта (!!!)
2
– тепловой выброс цементного завода (не пожар)1
2
Слайд 22
Дешифрование дыма
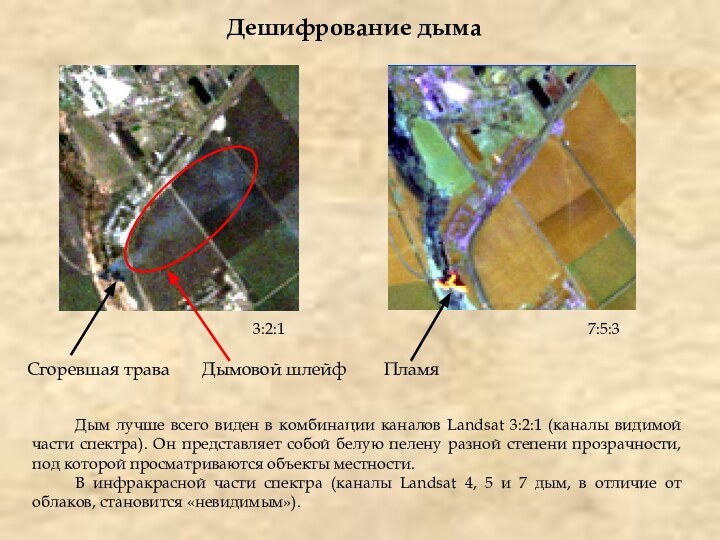
Дым лучше всего виден в комбинации каналов
Landsat 3:2:1 (каналы видимой части спектра). Он представляет собой
белую пелену разной степени прозрачности, под которой просматриваются объекты местности.В инфракрасной части спектра (каналы Landsat 4, 5 и 7 дым, в отличие от облаков, становится «невидимым»).
3:2:1
7:5:3
Пламя
Сгоревшая трава
Дымовой шлейф
Слайд 23
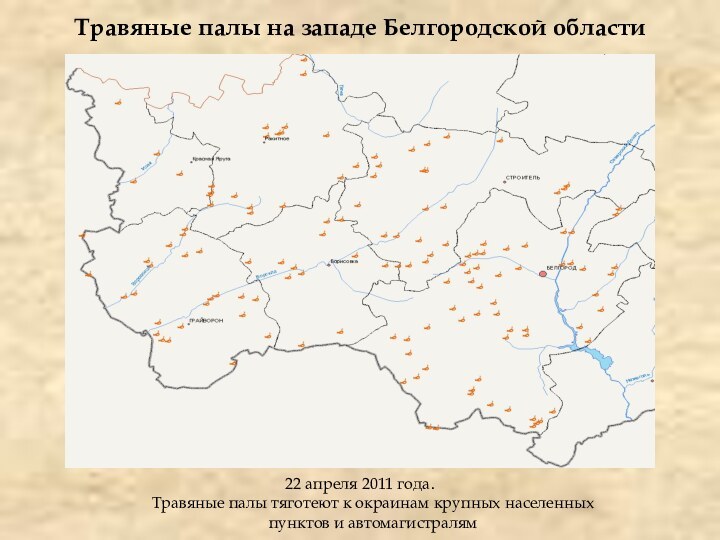
Травяные палы на западе Белгородской области
22 апреля 2011
года.
Травяные палы тяготеют к окраинам крупных населенных пунктов и
автомагистралям
Слайд 24
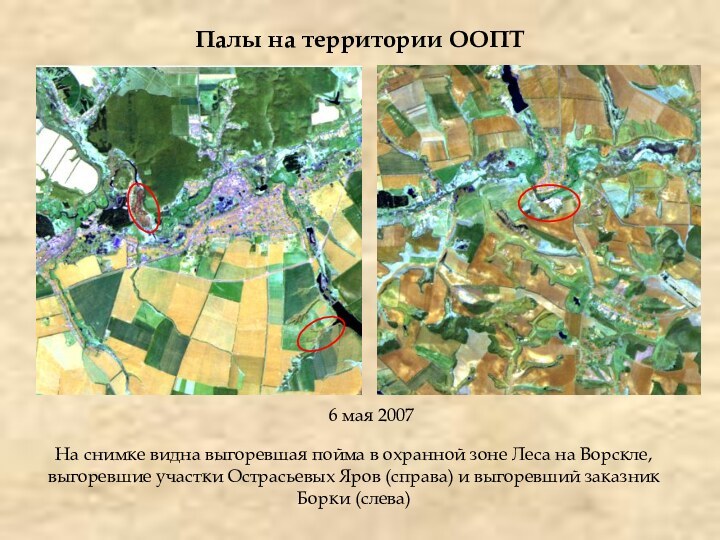
Палы на территории ООПТ
6 мая 2007
На снимке видна
выгоревшая пойма в охранной зоне Леса на Ворскле, выгоревшие
участки Острасьевых Яров (справа) и выгоревший заказник Борки (слева)
Слайд 25
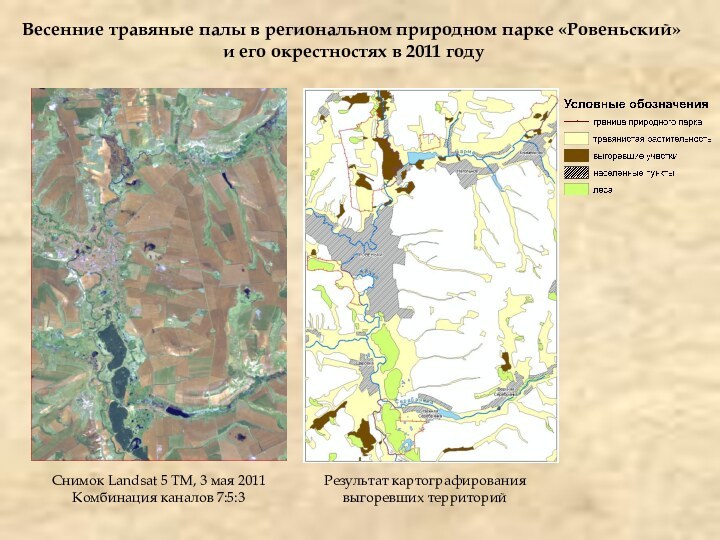
Весенние травяные палы в региональном природном парке «Ровеньский»
и его окрестностях в 2011 году
Снимок Landsat 5 TM,
3 мая 2011Комбинация каналов 7:5:3
Результат картографирования выгоревших территорий