Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике на тему Правильные многогранники

Содержание

Многогранник называется правильным, если все его грани – равные между собой правильные многоугольники, из каждой его вершины выходит одинаковое число ребер и все двугранные углы равны.
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Многогранник называется правильным, если все его грани – равные между собой правильные Существуют пять типов правильных многогранников: тетраэдр (треугольная пирамида) гексаэдр (куб) октаэдр икосаэдр додекаэдрdemo Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех Элементы симметрии:Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Элементы симметрии: Куб имеет центр симметрии - центр куба, 9 осей симметрии Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех Элементы симметрии: Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти Элементы симметрии: Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 Более двух тысяч лет многих привлекает эстетическое начало лежащее в основе правильных Сальвадор Дали «Тайная вечеря» АВТОРДОЛГОВА ГАЛИНА ЛЬВОВНАПреподаватель математикиУльяновского педагогического колледжа 4
Слайды презентации

Слайд 2
Многогранник называется правильным, если все его грани –

Многогранник называется правильным, если все его грани – равные между собой

равные между собой правильные многоугольники, из каждой его вершины

выходит одинаковое число ребер и все двугранные углы равны.

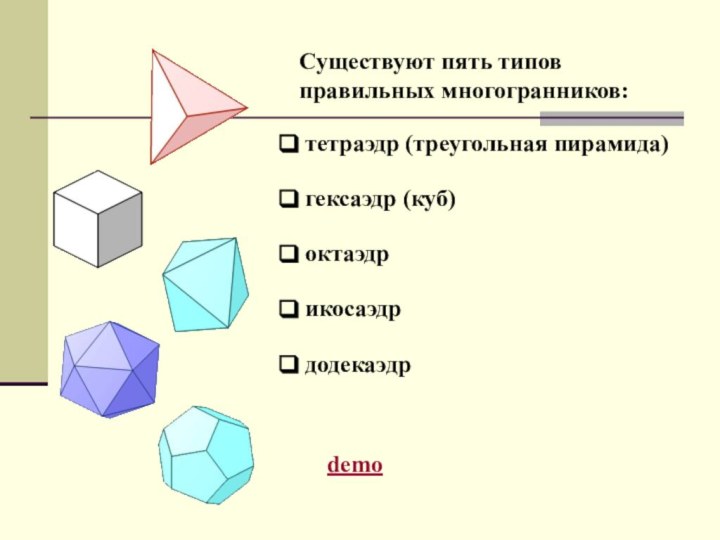
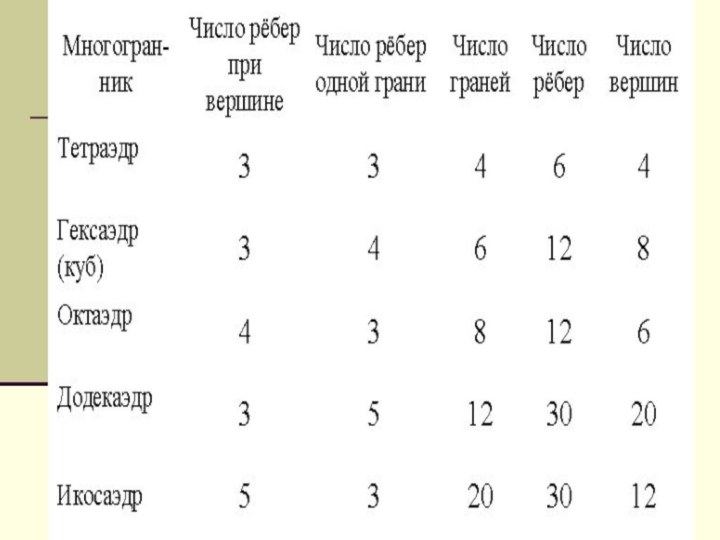
Слайд 3 Существуют пять типов правильных многогранников:
тетраэдр (треугольная

Существуют пять типов правильных многогранников: тетраэдр (треугольная пирамида) гексаэдр (куб) октаэдр икосаэдр додекаэдрdemo

пирамида)
гексаэдр (куб)
октаэдр
икосаэдр
додекаэдр
demo

Слайд 4
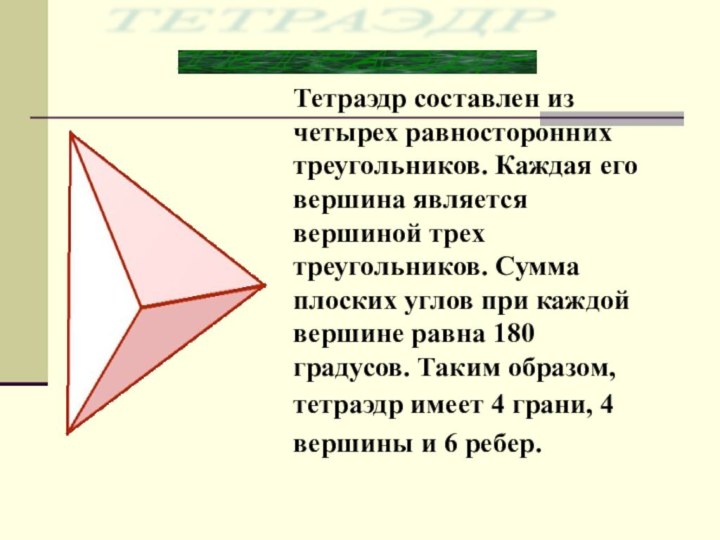
Тетраэдр составлен из четырех равносторонних треугольников. Каждая его

Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной

вершина является вершиной трех треугольников. Сумма плоских углов при

каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.

ТЕТРАЭДР

Слайд 5 Элементы симметрии:
Тетраэдр не имеет центра симметрии, но имеет

Элементы симметрии:Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии

3 оси симметрии и 6 плоскостей симметрии.

Радиус описанной сферы:



Радиус вписанной сферы:

Площадь поверхности:

Объем тетраэдра:


Слайд 6 Куб составлен из шести квадратов. Каждая его вершина

Куб составлен из шести квадратов. Каждая его вершина является вершиной трех

является вершиной трех квадратов. Сумма плоских углов при каждой

вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.

КУБ(ГЕКСАЭДР)

Слайд 7 Элементы симметрии:
Куб имеет центр симметрии - центр

Элементы симметрии: Куб имеет центр симметрии - центр куба, 9 осей

куба, 9 осей симметрии и 9 плоскостей симметрии.

Радиус

описанной сферы:

Радиус вписанной сферы:

Площадь поверхности куба:

Объем куба:  

 


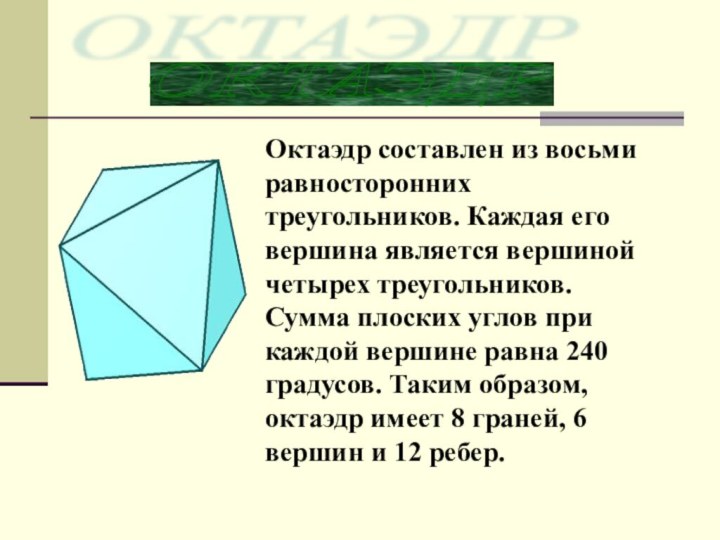
Слайд 8 Октаэдр составлен из восьми равносторонних треугольников. Каждая его

Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной

вершина является вершиной четырех треугольников. Сумма плоских углов при

каждой вершине равна 240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.

ОКТАЭДР

Слайд 9
Элементы симметрии:
Октаэдр имеет центр симметрии - центр

Элементы симметрии: Октаэдр имеет центр симметрии - центр октаэдра, 9 осей

октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Радиус

описанной сферы:

Радиус вписанной сферы:


:

Объем октаэдра:

Площадь поверхности:




:


Слайд 10
Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его

Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной

вершина является вершиной пяти треугольников. Сумма плоских углов при

каждой вершине равна 300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.

ИКОСАЭДР

Слайд 11 Элементы симметрии:
Икосаэдр имеет центр симметрии - центр

Элементы симметрии: Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей

икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус

описанной сферы:

Радиус вписанной сферы:

Объем икосаэдра:




Площадь поверхности:


Слайд 12
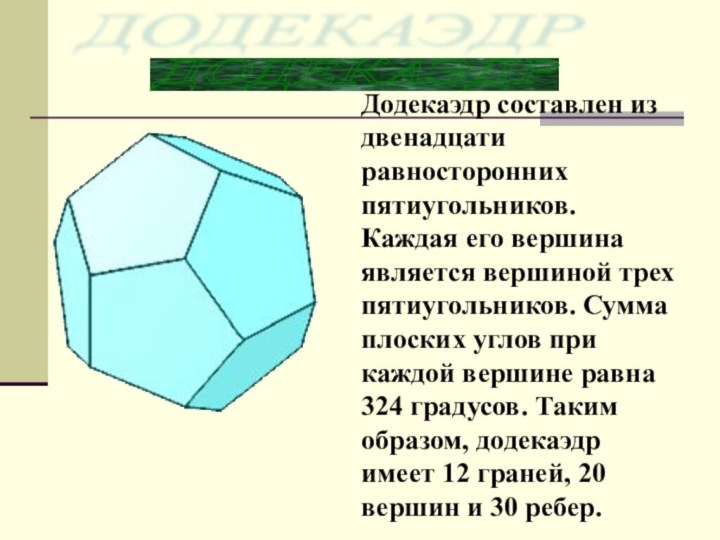
Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его

Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной

вершина является вершиной трех пятиугольников. Сумма плоских углов при

каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.

ДОДЕКАЭДР

Слайд 13 Додекаэдр имеет центр симметрии - центр додекаэдра, 15

Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и

осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:


Радиус вписанной сферы:

Площадь поверхности:

Объем додекаэдра:

Элементы симметрии:

Слайд 14

Слайд 15 Более двух тысяч лет многих привлекает эстетическое начало

Более двух тысяч лет многих привлекает эстетическое начало лежащее в основе

лежащее в основе правильных многогранников .Об этом свидетельствует картина

испанского художника Сальвадора Дали «Тайная вечеря».

Слайд 16 Сальвадор Дали «Тайная вечеря»

Сальвадор Дали «Тайная вечеря»
  • Имя файла: prezentatsiya-po-matematike-na-temu-pravilnye-mnogogranniki.pptx
  • Количество просмотров: 155
  • Количество скачиваний: 0
- Предыдущая Презентация Площади подобных фигур
Следующая - Презентация к уроку русского языка на тему: Как написать поздравительную открытку (3 Класс)

Похожие презентации

Откладывание вектора от данной точки Откладывание вектора от данной точки 199
Параллельный перенос Параллельный перенос 173
Презентация по геометрии 7 класс Равнобедренный треугольник Презентация по геометрии 7 класс Равнобедренный треугольник 155
Сфера и шар Сфера и шар 169
Угол между двумя прямыми Угол между двумя прямыми 148
Задачи на готовых чертежах Задачи на готовых чертежах 180
Теорема эйлера Теорема эйлера 191
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник 175
Начальные геометрические сведения Начальные геометрические сведения 165
Взаимное расположение прямой и плоскости. Признак параллельной прямой и плоскости Взаимное расположение прямой и плоскости. Признак параллельной прямой и плоскости 180
Обьёмные тела и многогранники Обьёмные тела и многогранники 143
Диктант по геометрии Параллелограмм8 класс Диктант по геометрии Параллелограмм8 класс 228
Параллелограмм 8 класс Параллелограмм 8 класс 205
Многогранники 9 класс Многогранники 9 класс 297
Презентация по геометрии на тему Площади простых фигур Презентация по геометрии на тему Площади простых фигур 62
Старые русские меры Старые русские меры 134
Теорема косинусов Теорема косинусов 133
Теорема Фалеса Теорема Фалеса 231
Эта замечательная парабола.. Эта замечательная парабола.. 158
Деление на равные части Деление на равные части 204
Конспект и презентация к уроку Площадь трапеции Конспект и презентация к уроку Площадь трапеции 149
Презентация по геометрии на тему Углы и отрезки, связанные с окружностью Презентация по геометрии на тему Углы и отрезки, связанные с окружностью 185
Презентация по геометрии 7 класс Презентация по геометрии 7 класс 153
Подібність трикутників Подібність трикутників 180
Решение простейших тригонометрических неравенств Решение простейших тригонометрических неравенств 160
Найти площадь криволинейной трапеции Найти площадь криволинейной трапеции 127
Презентация по геометрии на тему Параллельность прямой и плоскости (10 класс) Презентация по геометрии на тему Параллельность прямой и плоскости (10 класс) 217
Тела вращения вокруг нас Тела вращения вокруг нас 172
Вписанные шары Вписанные шары 210
Параллельность прямой и плоскости Параллельность прямой и плоскости 234