- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Смежные и вертикальные углы
Содержание
- 2. Определение.В определении смежных углов содержатся три условия:
- 3. Проведем луч OD Являются ли смежными углы:
- 4. Дан произвольный ∠(аb), отличный от развернутого. Сколько существует углов, смежных с ним? abcdd
- 5. Теорема. Сумма смежных углов равна 180°..1) Так
- 6. 1) Углы, смежные равным углам, равны между
- 7. Пусть x – коэффициент пропорциональности, тогда, ∠BOC
- 8. Сформулируйте утверждение, обратное теореме о смежных углах.
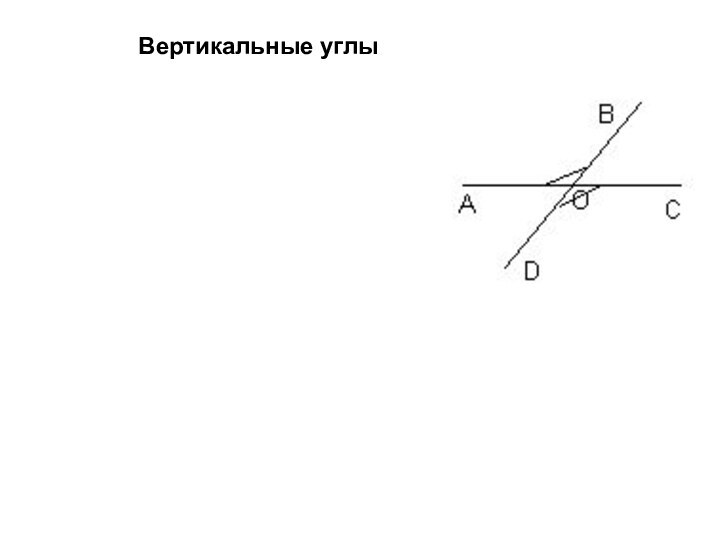
- 9. Вертикальные углы
- 10. Теорема. Вертикальные углы равны.Дано: ∠AOB и ∠COD
- 11. Сформулируйте утверждение, обратное свойству вертикальных углов. Верно ли оно?
- 12. Скачать презентацию
- 13. Похожие презентации
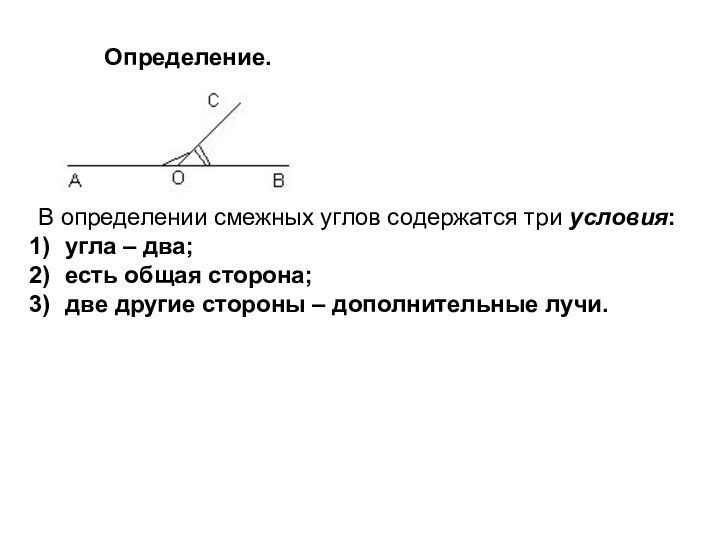
Определение.В определении смежных углов содержатся три условия: угла – два; есть общая сторона; две другие стороны – дополнительные лучи.




Слайд 2
Определение.
В определении смежных углов содержатся три условия:
угла
– два;
дополнительные лучи.
Слайд 3
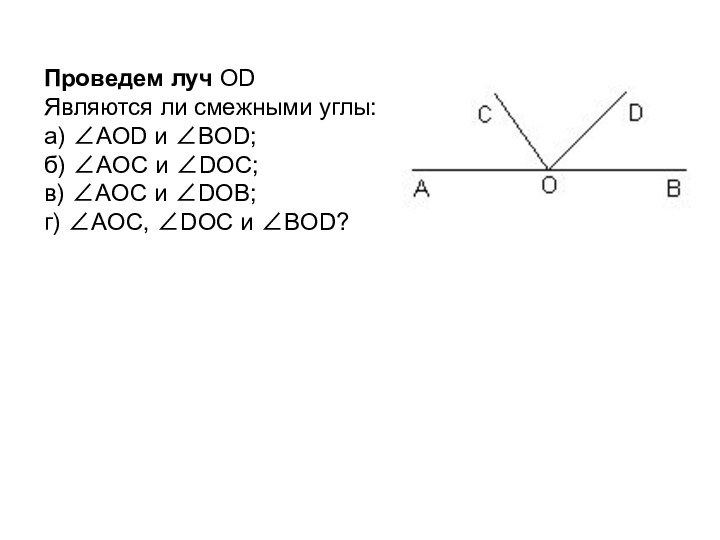
Проведем луч OD
Являются ли смежными углы:
а)
∠AOD и ∠BOD;
б) ∠AOС и ∠DOС;
в) ∠AOС
и ∠DOВ; г) ∠AOС, ∠DOС и ∠BOD?
Слайд 4
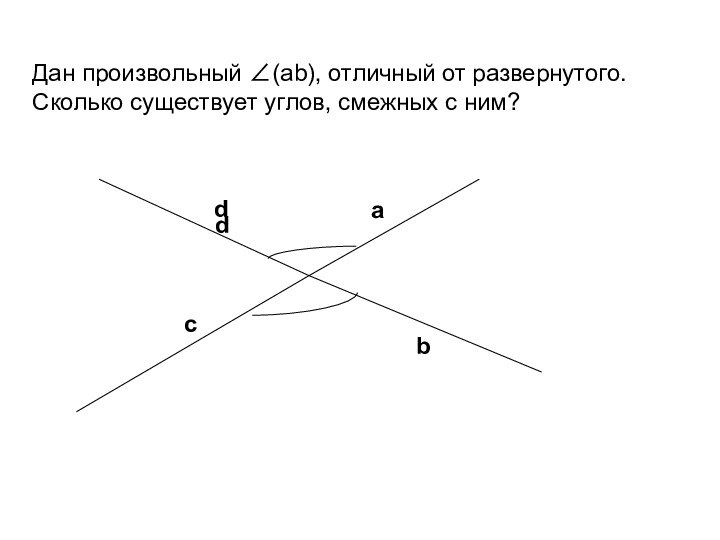
Дан произвольный ∠(аb), отличный от развернутого.
Сколько существует
углов, смежных с ним?
a
b
c
d
d
Слайд 5
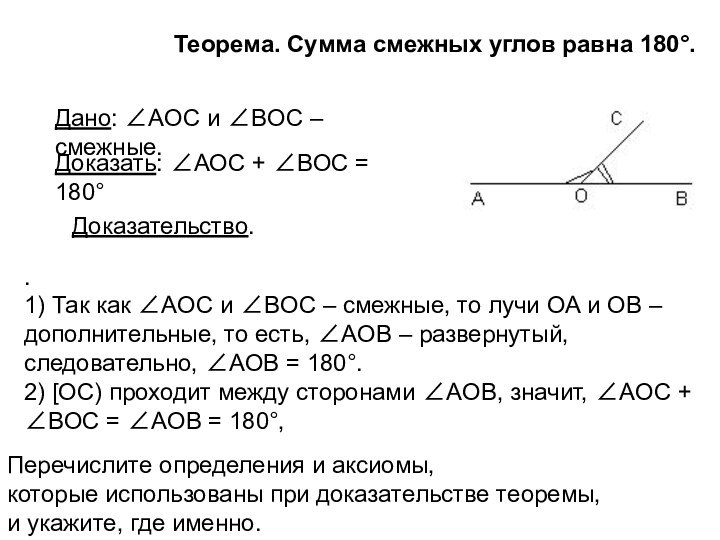
Теорема. Сумма смежных углов равна 180°.
.
1) Так как
∠AOC и ∠BOC – смежные, то лучи ОА и
ОВ – дополнительные, то есть, ∠AOB – развернутый, следовательно, ∠AOB = 180°.2) [OC) проходит между сторонами ∠AOB, значит, ∠AOC + ∠BOC = ∠AOB = 180°,
Дано: ∠AOC и ∠BOC – смежные.
Доказать: ∠AOC + ∠BOC = 180°
Доказательство.
Перечислите определения и аксиомы,
которые использованы при доказательстве теоремы,
и укажите, где именно.
Слайд 6
1) Углы, смежные равным углам, равны между собой.
2)
Угол, смежный прямому углу – прямой,
смежный острому –
тупой, смежный тупому – острый. А смежный развернутому?
Следствия из теоремы
Слайд 7
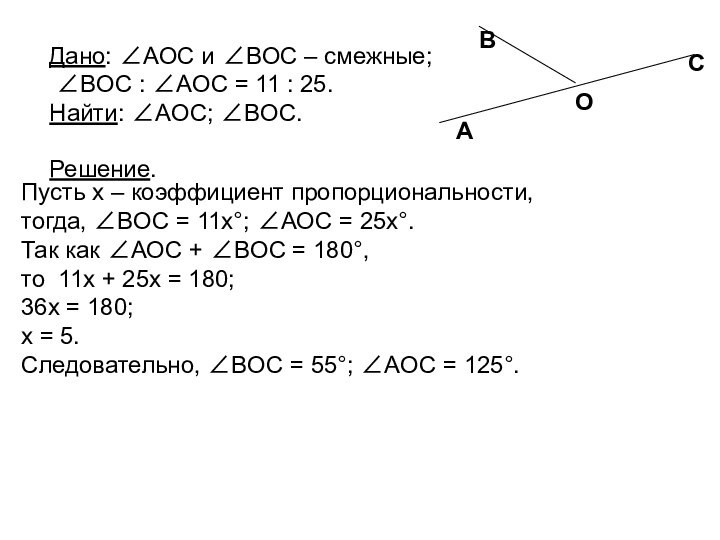
Пусть x – коэффициент пропорциональности,
тогда, ∠BOC =
11x°; ∠AOC = 25x°.
Так как ∠AOC + ∠BOC
= 180°, то 11x + 25x = 180;
36x = 180;
x = 5.
Следовательно, ∠BOC = 55°; ∠AOC = 125°.
Дано: ∠AOC и ∠BOC – смежные;
∠BOC : ∠AOC = 11 : 25.
Найти: ∠AOC; ∠BOC.
Решение.
A
O
C
B
Слайд 8
Сформулируйте утверждение,
обратное теореме о смежных углах.
Верно
ли оно?
Станет ли оно верным, если добавить,
что
у данных углов есть общая сторона? Что еще необходимо добавить в условие,
чтобы оно стало верным?
Слайд 10
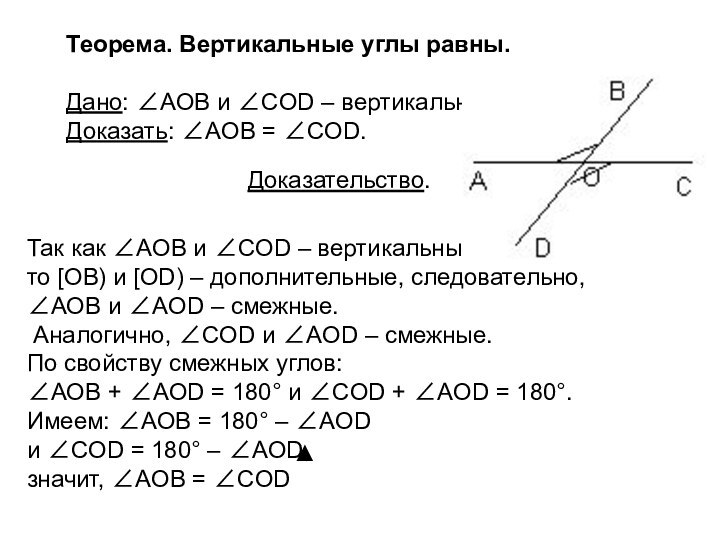
Теорема. Вертикальные углы равны.
Дано: ∠AOB и ∠COD –
вертикальные.
Доказать: ∠AOB = ∠COD.
Так как ∠AOB и ∠COD –
вертикальные, то [OB) и [OD) – дополнительные, следовательно,
∠AOB и ∠AOD – смежные.
Аналогично, ∠COD и ∠AOD – смежные.
По свойству смежных углов:
∠AOB + ∠AOD = 180° и ∠COD + ∠AOD = 180°.
Имеем: ∠AOB = 180° – ∠AOD
и ∠COD = 180° – ∠AOD,
значит, ∠AOB = ∠COD
Доказательство.
▲