- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Соотношения между сторонами и углами треугольника 7 класс
Содержание
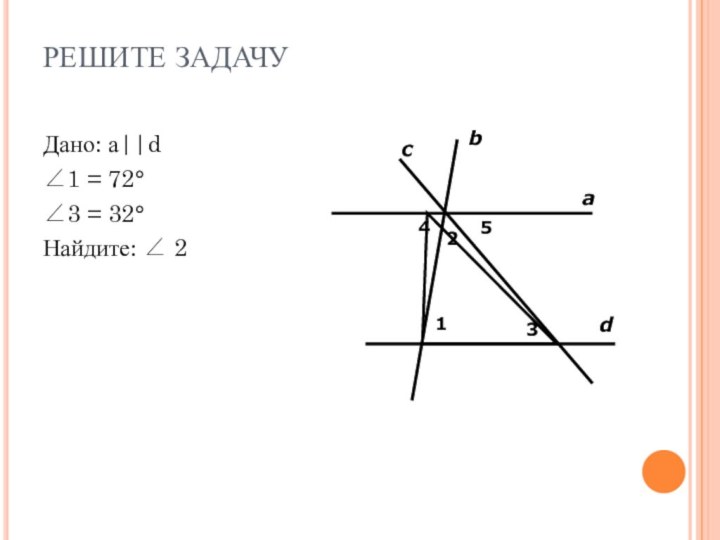
- 2. РЕШИТЕ ЗАДАЧУДано: а||d∠1 = 72°∠3 = 32°Найдите: ∠ 2а12354cdb
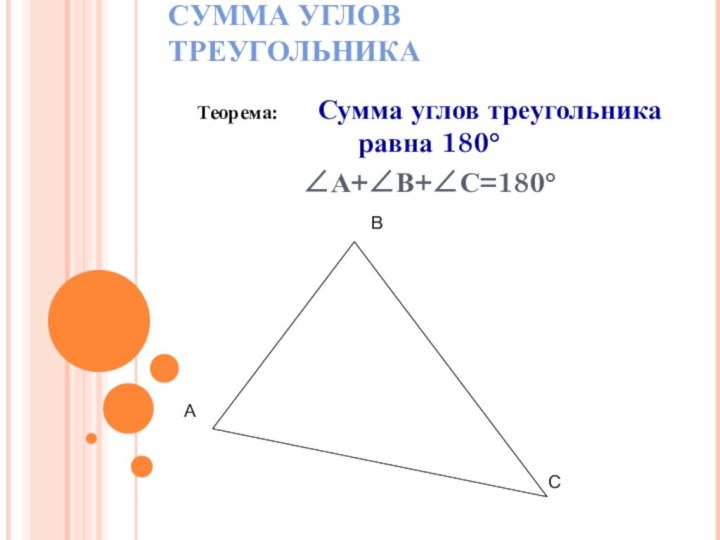
- 3. СУММА УГЛОВ ТРЕУГОЛЬНИКАТеорема: Сумма углов треугольника равна 180°∠А+∠В+∠С=180°АВС
- 5. ЗАДАЧИНайти: ∠ВНайти: ∠А, ∠В, ∠СДано: Δ MNKМК
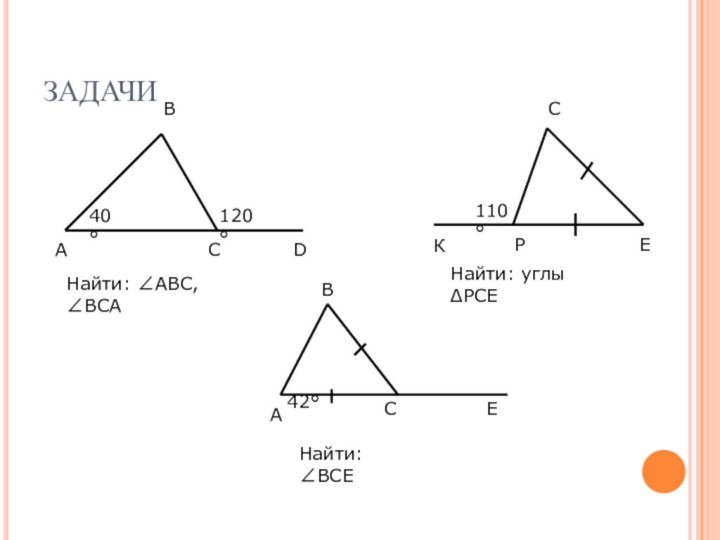
- 6. ЗАДАЧИНайти: ∠АВС, ∠ВСАНайти: углы ΔРСЕНайти: ∠ВСЕ
- 7. ВНЕШНИЙ УГОЛОпределение: Угол смежный с каким-нибудь
- 8. СВОЙСТВО ВНЕШНЕГО УГЛАВнешний угол треугольника равен сумме
- 9. ЗАДАЧА: РЕШИТЕ ЗАДАЧУ, ИСПОЛЬЗУЯ СВОЙСТВО
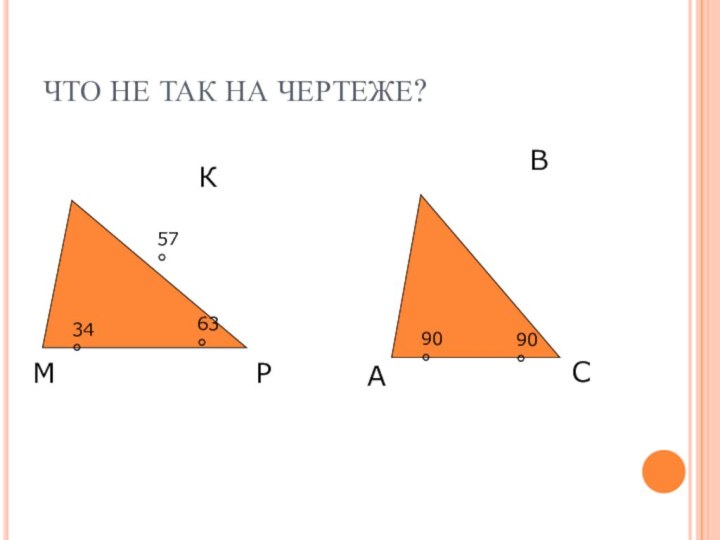
- 10. ЧТО НЕ ТАК НА ЧЕРТЕЖЕ?
- 11. ВИДЫ ТРЕУГОЛЬНИКОВ1. ОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
- 12. ВИДЫ ТРЕУГОЛЬНИКА2. Тупоугольный треугольник (один из углов тупой, два других острые)АВС
- 13. ВИДЫ ТРЕУГОЛЬНИКА3. Прямоугольный треугольник
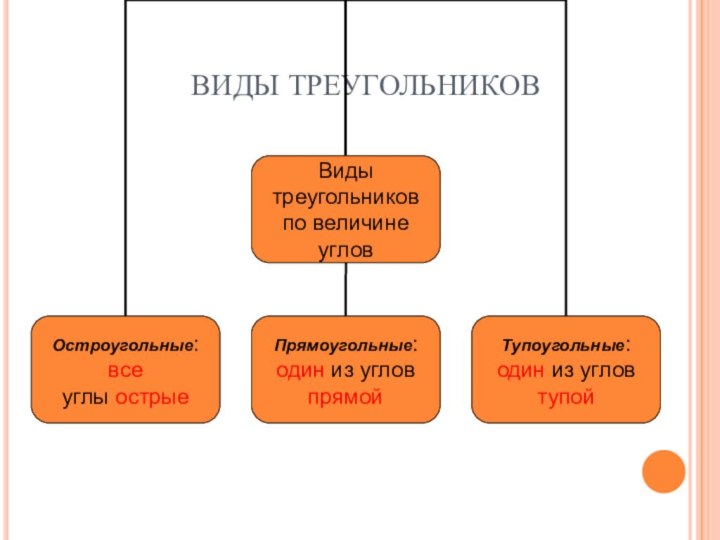
- 14. ВИДЫ ТРЕУГОЛЬНИКОВ
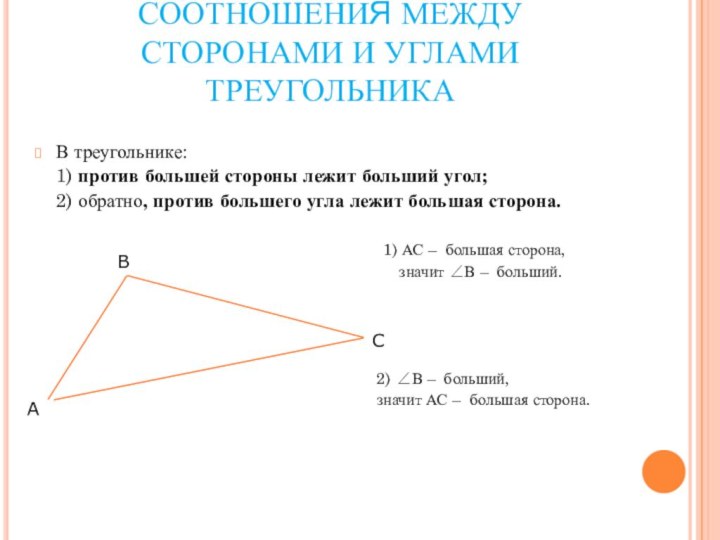
- 15. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКАВ треугольнике:
- 16. СЛЕДСТВИЯ1. В прямоугольном треугольнике гипотенуза больше
- 17. НЕРАВЕНСТВО ТРЕУГОЛЬНИКАТеорема: Каждая сторона треугольника меньше суммы
- 18. Скачать презентацию
- 19. Похожие презентации
РЕШИТЕ ЗАДАЧУДано: а||d∠1 = 72°∠3 = 32°Найдите: ∠ 2а12354cdb





Слайд 4
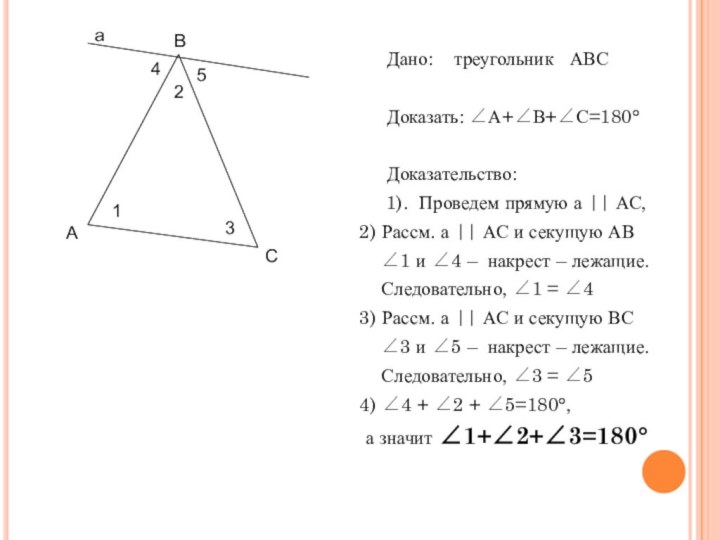
Дано: треугольник АВС
Доказать: ∠А+∠В+∠С=180°
Доказательство:
1). Проведем прямую а || АС,
2) Рассм. а || АС и секущую АВ
∠1 и ∠4 – накрест – лежащие.
Следовательно, ∠1 = ∠4
3) Рассм. а || АС и секущую ВС
∠3 и ∠5 – накрест – лежащие.
Следовательно, ∠3 = ∠5
4) ∠4 + ∠2 + ∠5=180°,
а значит ∠1+∠2+∠3=180°
А
В
С
а
1
3
2
4
5
Слайд 5
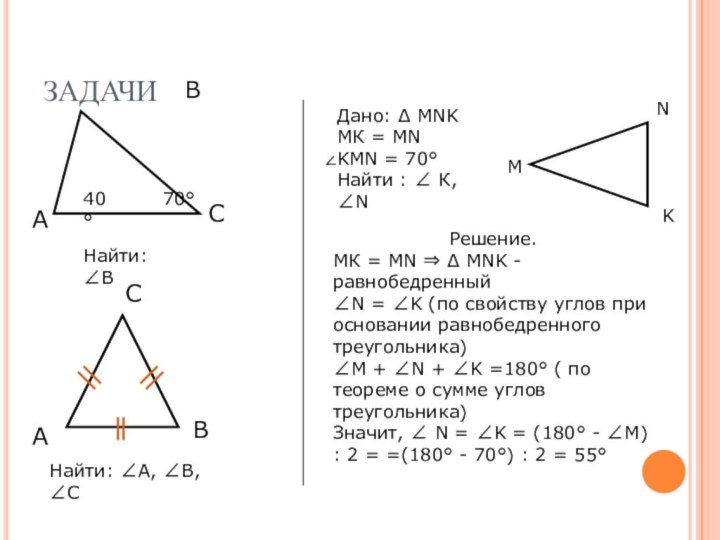
ЗАДАЧИ
Найти: ∠В
Найти: ∠А, ∠В, ∠С
Дано: Δ MNK
МК =
MN
KMN = 70°
Найти : ∠ К, ∠N
Решение.
МК = MN
⇒ Δ MNK - равнобедренный∠N = ∠K (по свойству углов при основании равнобедренного треугольника)
∠M + ∠N + ∠K =180° ( по теореме о сумме углов треугольника)
Значит, ∠ N = ∠K = (180° - ∠M) : 2 = =(180° - 70°) : 2 = 55°
Слайд 7
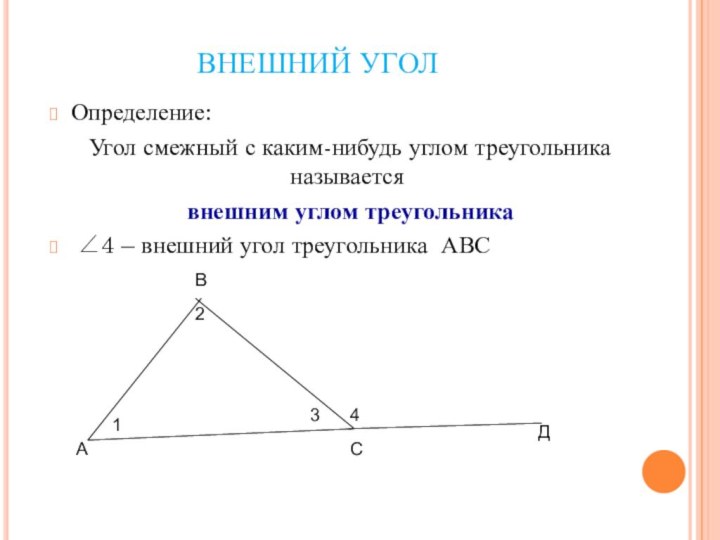
ВНЕШНИЙ УГОЛ
Определение:
Угол смежный с каким-нибудь углом
треугольника называется
внешним углом треугольника
∠4
– внешний угол треугольника АВСА
В
С
4
1
2
3
Д
Слайд 8
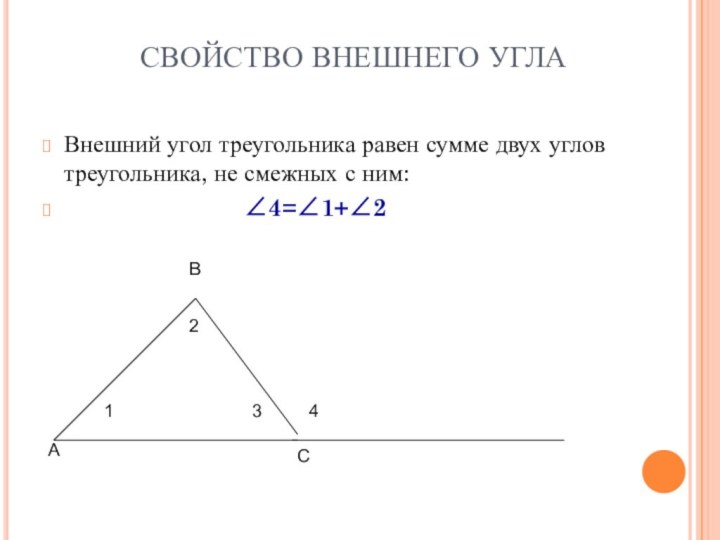
СВОЙСТВО ВНЕШНЕГО УГЛА
Внешний угол треугольника равен сумме двух
углов треугольника, не смежных с ним:
∠4=∠1+∠2А
В
С
4
1
2
3
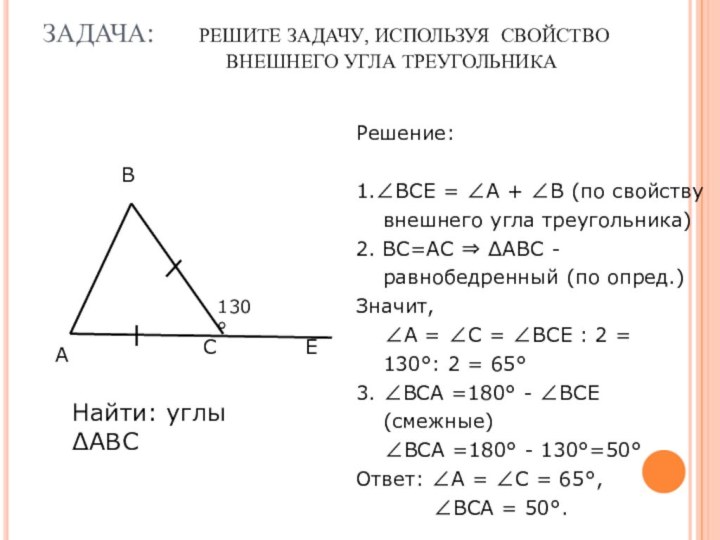
Слайд 9 ЗАДАЧА: РЕШИТЕ ЗАДАЧУ, ИСПОЛЬЗУЯ СВОЙСТВО
ВНЕШНЕГО УГЛА ТРЕУГОЛЬНИКА
Найти: углы ΔАВС
Решение:
1.∠ВСЕ = ∠А + ∠В (по свойству внешнего угла треугольника)
2. ВС=АС ⇒ ΔАВС - равнобедренный (по опред.)
Значит,
∠А = ∠С = ∠ВСЕ : 2 = 130°: 2 = 65°
3. ∠ВСА =180° - ∠ВСЕ (смежные)
∠ВСА =180° - 130°=50°
Ответ: ∠А = ∠С = 65°,
∠ВСА = 50°.
Слайд 13
ВИДЫ ТРЕУГОЛЬНИКА
3. Прямоугольный треугольник
(один из углов прямой, а два других
острые)АС и СВ – катеты
АВ – гипотенуза
А
В
С
Слайд 15
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
В треугольнике:
1) против большей стороны лежит больший угол;
2) обратно, против большего угла лежит большая сторона.1) АС – большая сторона,
значит ∠В – больший.
2) ∠В – больший,
значит АС – большая сторона.
А
С
В
Слайд 16
СЛЕДСТВИЯ
1. В прямоугольном треугольнике гипотенуза больше катета.
Признак равнобедренного треугольника:
2. Если в треугольнике два
угла равны,то треугольник равнобедренный
Слайд 17
НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
Теорема: Каждая сторона треугольника меньше суммы двух
других сторон.
Дано: треугольник АВС.
Доказать: АВ
на продолжении стороны АССД=ВС. Треугольник ВСД равнобедренный∠1=∠2, а в
треугольнике АВД ∠АВД>∠1, значит ∠АВД>∠2, то АВ<АД.
Но АД=АС+СД=АС+СВ, поэтому АВ<АС+ВС
2
1
В
А
С
Д