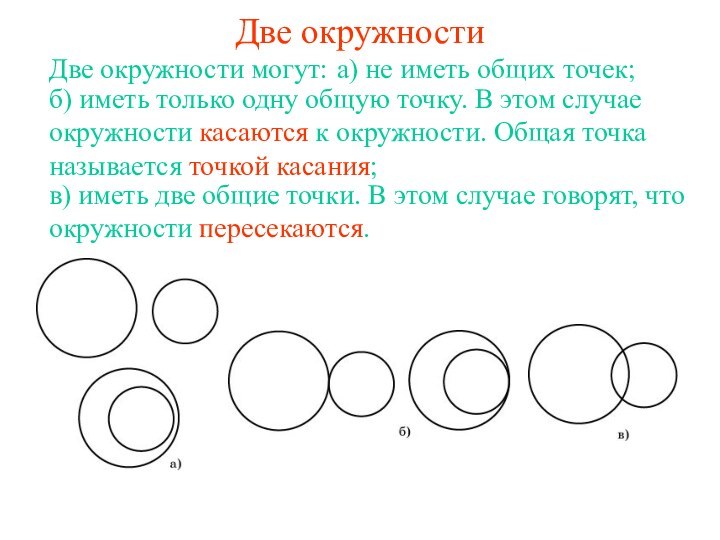
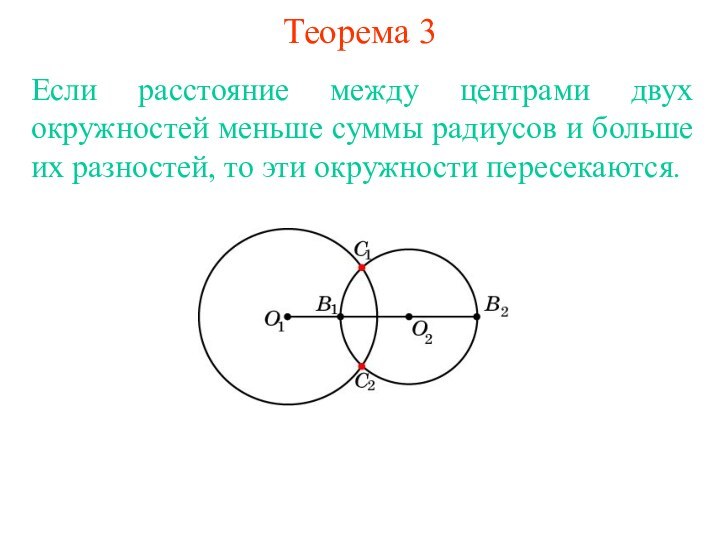
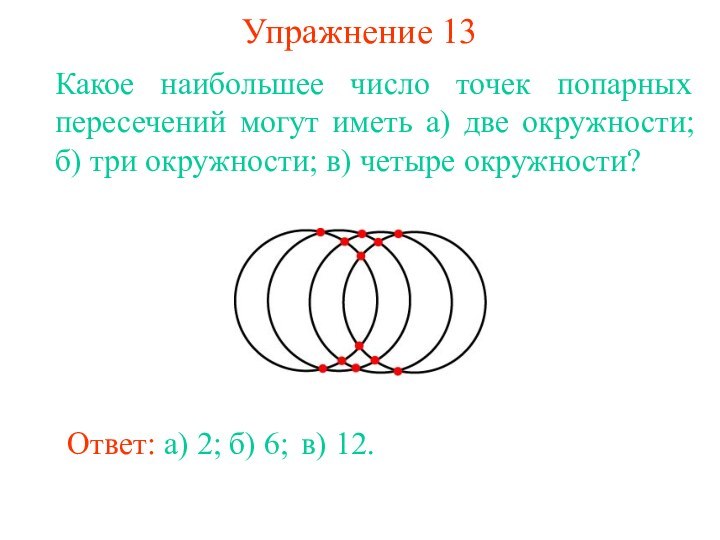
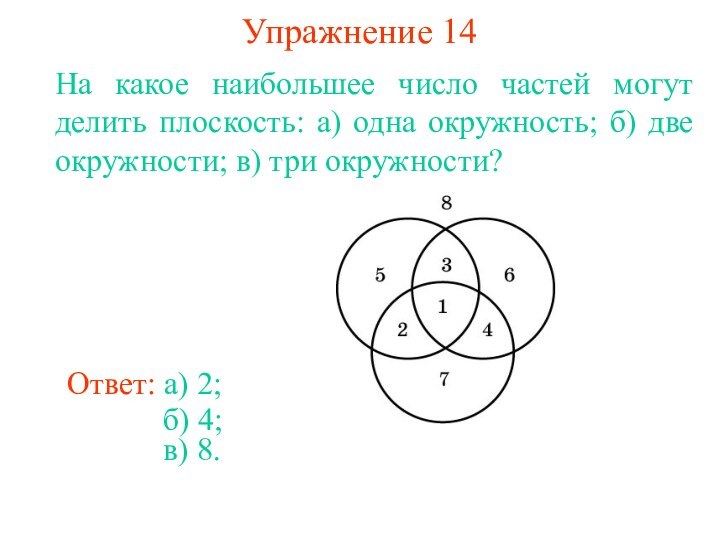
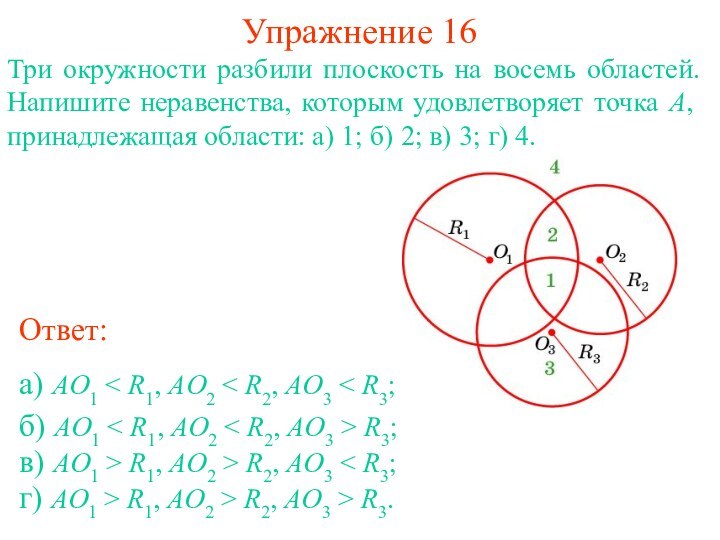
суммы их радиусов или меньше их разности, то эти
окружности не имеют общих точек.Доказательство. Пусть даны две окружности с центрами в точках О1, О2 и радиусами соответственно R1, R2, R1 + R2 < O1O2. Рассмотрим точку С на первой окружности, О1С = R1. Тогда O2C O1O2 - O1C > R1 + R2 - R1 = R2 и, следовательно, точка С не принадлежит второй окружности. Значит, эти окружности не имеют общих точек. Аналогичным образом доказывается, что если O1O2 < R1- R2 (R1 > R2), то окружности также не имеют общих точек.