- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему урока геометрии в 9 классе по теме Окружность (повторение учебного материала при подготовке к ОГЭ)
Содержание
- 2. Успешная сдача ОГЭ — первая ступень к выбору будущей профессии.
- 3. Какие из утверждений верны? Радиусы одной окружности
- 4. Закончите теоремы.Вписанный угол …Касательная к окружности …Вписанные
- 5. Какова тема сегодняшнего урока?
- 6. Окружность.
- 7. Урок решения ключевых задач.
- 8. Какая на ваш взгляд цель урока?
- 9. Цель урока:уметь решать задачи по теме «Окружность».
- 10. Вопросы и претензии:Я не
- 11. Вы должны уметь:прочитав внимательно задачу несколько раз,хорошо
- 13. А
- 14. А
- 15. А
- 16. А
- 17. А
- 18. Окружность, проходящая через вершины А и В
- 19. • СМКА В
- 20. • СМКА
- 21. • СМКА
- 22. • СМКА
- 23. • СМКА
- 24. •А
- 26. В АНСКРО
- 27. В
- 28. В
- 29. В
- 30. В
- 32. В СКАРМ•
- 33. В СКАРМ•Дано:ΔАВС, окр(О;R), АМ, АР, ВС
- 34. В СКАРМ•Дано:ΔАВС, окр(О;R), АМ, АР, ВС
- 35. В СКАРМ•Дано:ΔАВС, окр(О;R), АМ, АР, ВС
- 36. В СКАРМ•Дано:ΔАВС, окр(О;R), АМ, АР, ВС
- 37. Устали?Какой вывод сделали после этого урока?
- 38. Чтобы решить задачу надо:прочитав внимательно задачу несколько
- 39. Скачать презентацию
- 40. Похожие презентации























Слайд 3
Какие из утверждений верны?
Радиусы одной окружности равны.
Все
хорды одной окружности равны.
Все диаметры равны.
Вписанные углы окружности равны.
Диаметр
— это хорда, проходящая через центр.
Слайд 4
Закончите теоремы.
Вписанный угол …
Касательная к окружности …
Вписанные углы
…
Если четырехугольник описан около окружности …
Отрезки касательных …
Если в
четырехугольник вписана окружность …Закончите теоремы.
Вписанный угол …
Касательная к окружности …
Вписанные углы …
Если четырехугольник описан около окружности …
Отрезки касательных …
Если в четырехугольник вписана окружность ...
Закончите теоремы.
Вписанный угол …
Касательная к окружности …
Вписанные углы …
Если четырехугольник описан около окружности …
Отрезки касательных …
Если в четырехугольник вписана окружность ...
Слайд 10
Вопросы и претензии:
Я не понимаю
задачу.
Как начертить чертеж?
А что здесь надо найти?
А как решать
эту задачу?
Слайд 11
Вы должны уметь:
прочитав внимательно задачу несколько раз,хорошо понять
ее условие;
самостоятельно выполнить чертеж (аккуратный и достаточно крупный);
записать условие
задачи;вспомнить теорию по данной теме;
решить задачу, опираясь на теорию.
Слайд 12
№1
Докажите, что окружность,
построенная на стороне остроугольного треугольника как на диаметре, пересекает две другие стороны в основаниях высот.
Слайд 15
А
•
СО
В
К
М
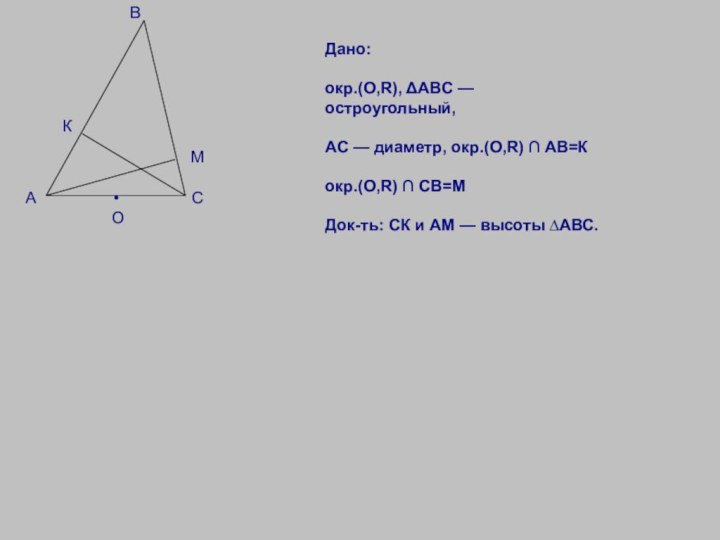
Дано:
окр.(О,R), ΔАВС — остроугольный,
АС — диаметр, окр.(О,R) ∩ АВ=К
окр.(О,R) ∩ СВ=М
Док-ть: СК и АМ — высоты ∆АВС.
Слайд 16
А
•
СО
В
К
М
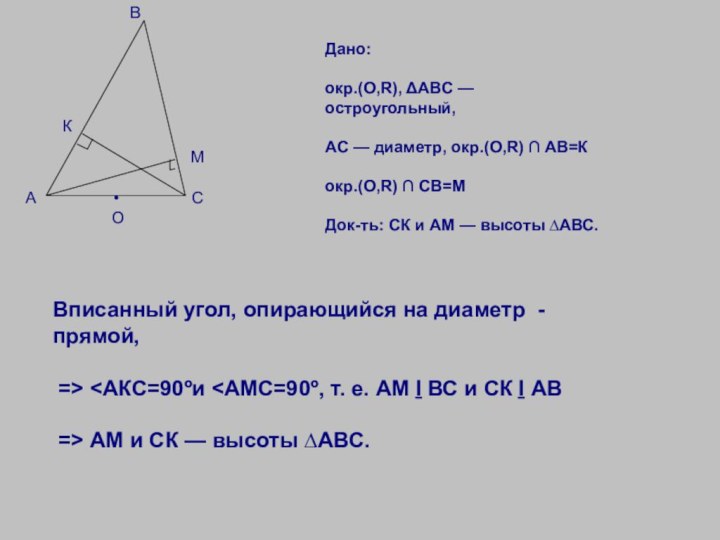
Дано:
окр.(О,R), ΔАВС — остроугольный,
АС — диаметр, окр.(О,R) ∩ АВ=К
окр.(О,R) ∩ СВ=М
Док-ть: СК и АМ — высоты ∆АВС.
Вписанный угол, опирающийся на диаметр - прямой,
=> <АКС=90ºи <АМС=90º, т. е. АМ ḻ ВС и СК ḻ АВ
=> АМ и СК — высоты ∆АВС.
Слайд 17
А
•
СО
В
Докажите, что окружность, построенная на
стороне остроугольного треугольника как
на диаметре, пересекает две другие стороны
в основаниях высот.
Почему остроугольного?
А если тупоугольный?
А если прямоугольный?
Слайд 18
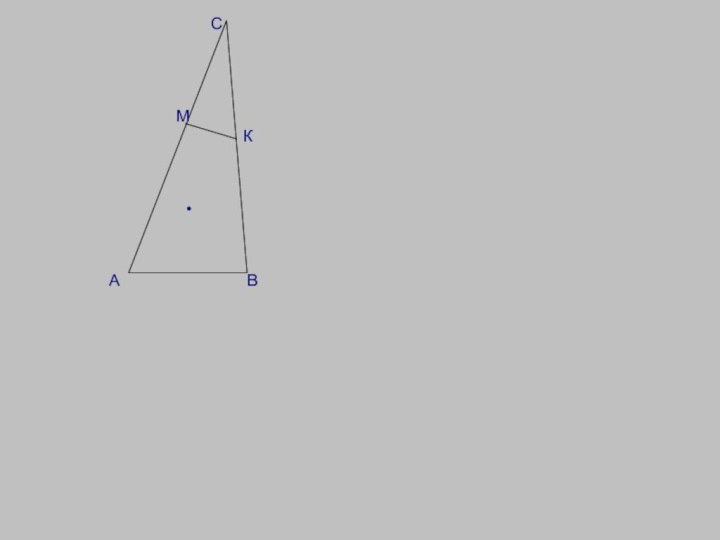
Окружность, проходящая через вершины А и В треугольника
АВС, пересекает стороны АС и ВС в точках М
и К соответственно. Докажите, что ∆АВС и ∆СКМ подобны.№2
Слайд 20
•
С
М
К
А
В
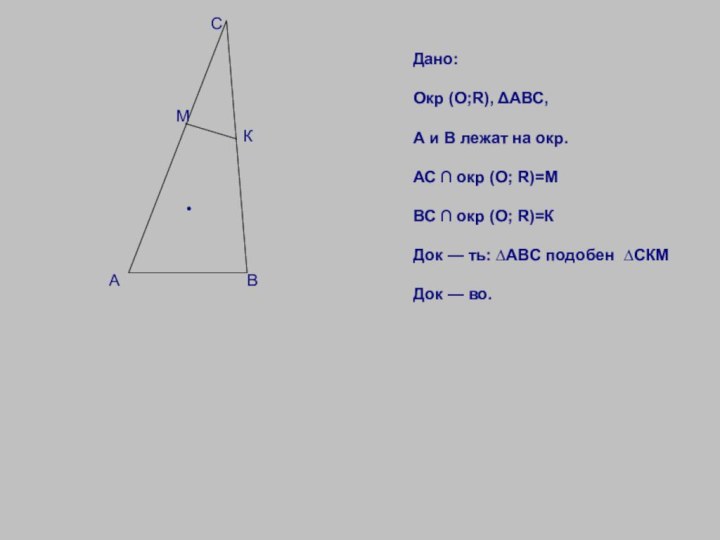
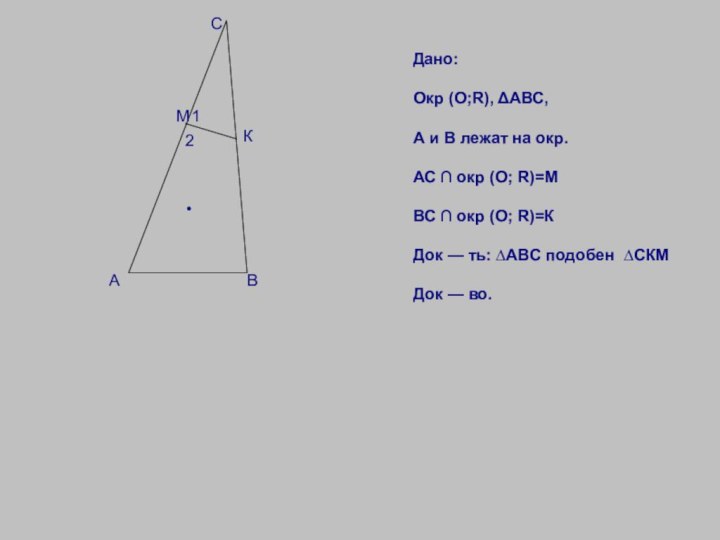
Дано:
Окр (О;R),
ΔАВС, А и В лежат на окр.
АС ∩ окр (О; R)=М
ВС ∩ окр (О; R)=К
Док — ть: ∆АВС подобен ∆СКМ
Док — во.
Слайд 21
•
С
М
К
А
В
1
2
Дано:
Окр
(О;R), ΔАВС, А и В лежат на окр.
АС ∩ окр (О; R)=М
ВС ∩ окр (О; R)=К
Док — ть: ∆АВС подобен ∆СКМ
Док — во.
Слайд 22
•
С
М
К
А
В
1
2
Дано:
Окр
(О;R), ΔАВС, А и В лежат на окр.
АС ∩ окр (О; R)=М
ВС ∩ окр (О; R)=К
Док — ть: ∆АВС подобен ∆СКМ
Док — во.
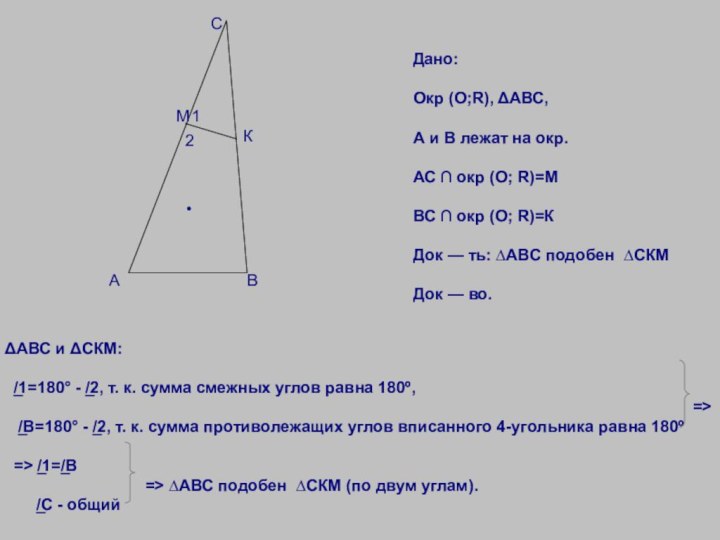
ΔАВС и ΔСКМ:
/̲1=180° - /̲2, т. к. сумма смежных углов равна 180º,
=>
/̲В=180° - /̲2, т. к. сумма противолежащих углов вписанного 4-угольника равна 180º
=> /̲1=/̲В
=> ∆АВС подобен ∆СКМ (по двум углам).
/̲С - общий
Слайд 23
•
С
М
К
А
В
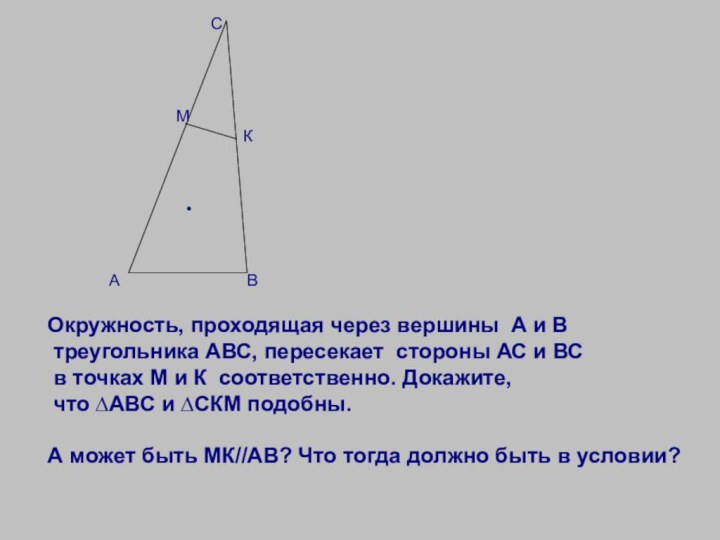
Окружность, проходящая
через вершины А и Втреугольника АВС, пересекает стороны АС и ВС
в точках М и К соответственно. Докажите,
что ∆АВС и ∆СКМ подобны.
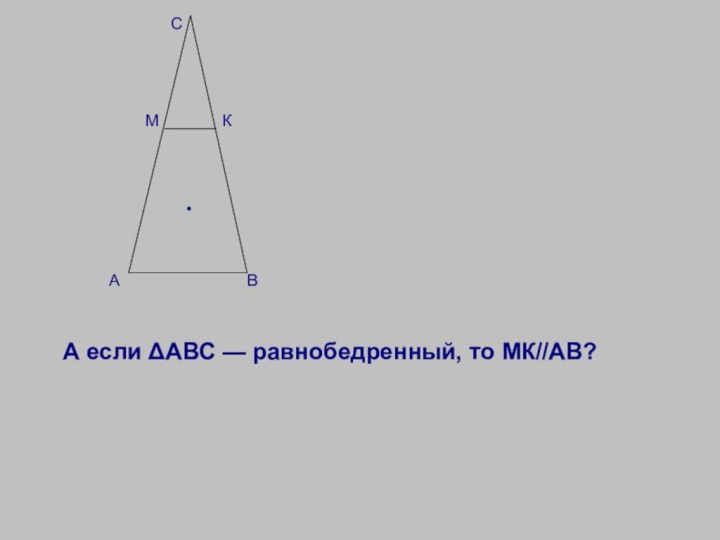
А может быть МК//АВ? Что тогда должно быть в условии?
Слайд 25
№3
Точка Н является основанием
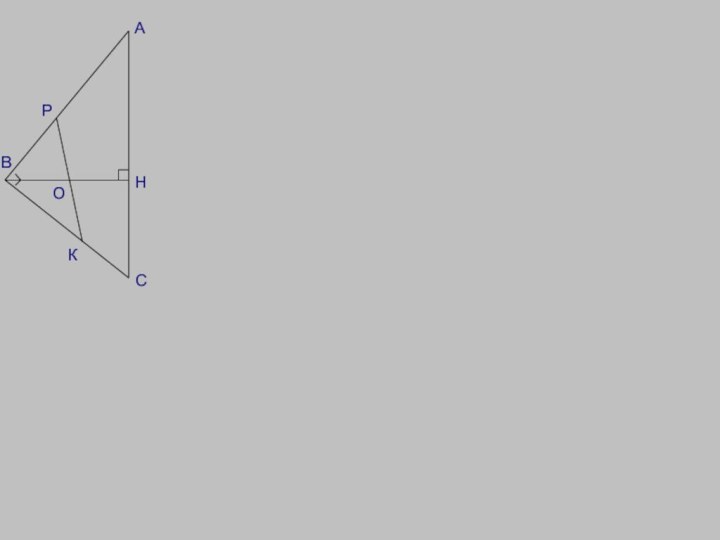
высоты ВН, проведенной из вершины прямого угла В прямоугольного треугольника АВС. Окружность с диаметром ВН пересекает стороны АВ и СВ в точках Р и К соответственно. Найдите ВН, если РК=37.
Слайд 27
В 37
А
Н
С
К
Р
О
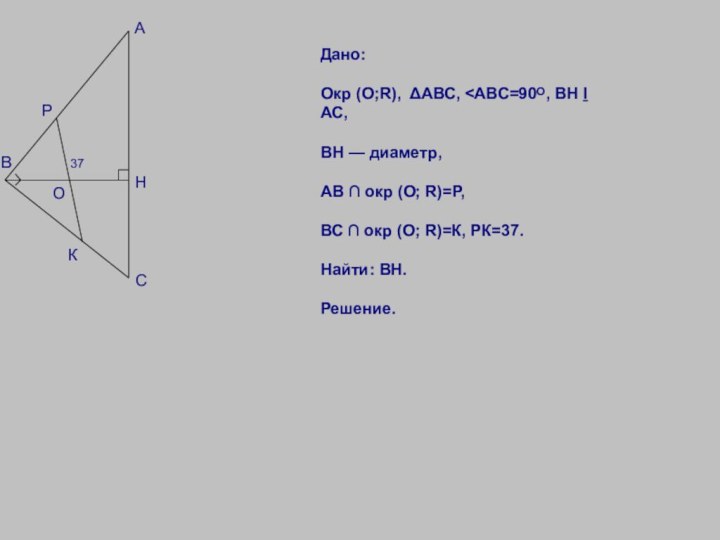
Дано:
Окр (О;R),
ΔАВС, <АВС=90ᴼ, ВН ḻ АС,ВН — диаметр,
АВ ∩ окр (О; R)=Р,
ВС ∩ окр (О; R)=К, РК=37.
Найти: ВН.
Решение.
Слайд 28
В
А
Н
С
К
Р
О
Дано:
Окр (О;R), ΔАВС,
<АВС=90ᴼ, ВН ḻ АС,ВН — диаметр,
АВ ∩ окр (О; R)=Р,
ВС ∩ окр (О; R)=К, РК=37.
Найти: ВН.
Решение.
37
половине дуги, на которую он опирается).
Слайд 29
В
А
Н
С
К
Р
О
Дано:
Окр (О;R), ΔАВС,
<АВС=90ᴼ, ВН ḻ АС,ВН — диаметр,
АВ ∩ окр (О; R)=Р,
ВС ∩ окр (О; R)=К, РК=37.
Найти: ВН.
Решение.
37
половине дуги, на которую он опирается).
ᴗРНК=180º, => РК — диаметр окружности, но и ВН — диаметр (по условию)
РК=ВН=37 как диаметры одной окружности.
Ответ: 37
Слайд 31
№4
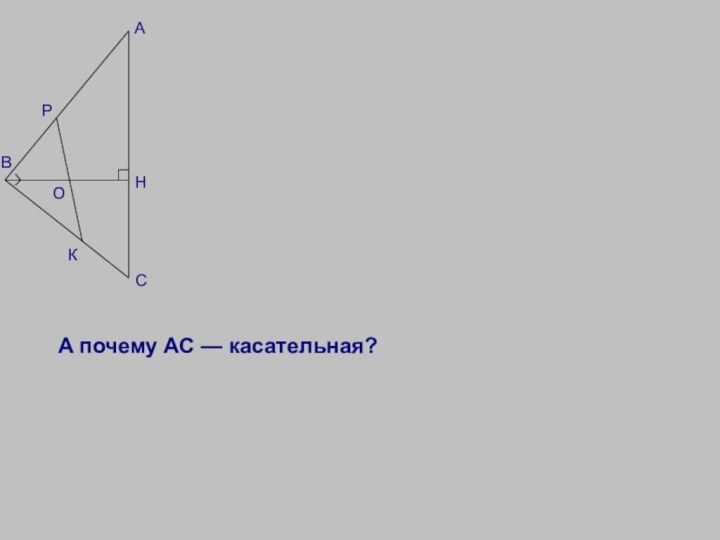
Окружность касается стороны
ВС треугольника АВС в точке К, а продолжений сторон АВ и АС — в точках Р и М соответственно. Докажите, что отрезок АР равен полупериметру ΔАВС.
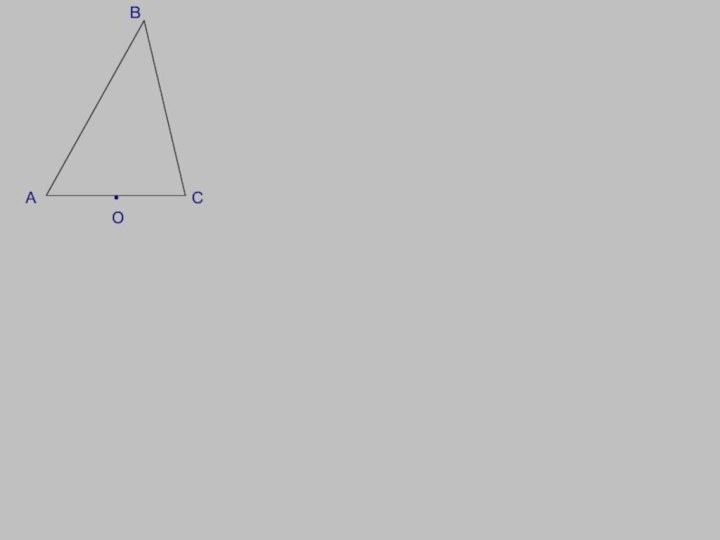
Слайд 33
В
С
К
А
Р
М
•
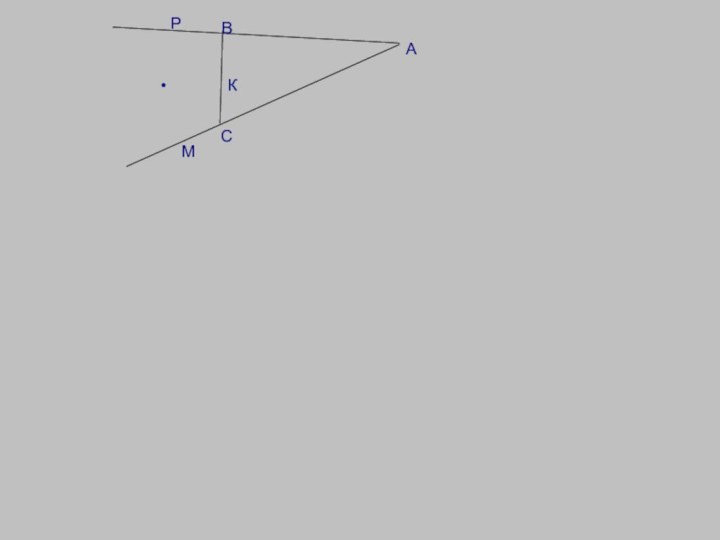
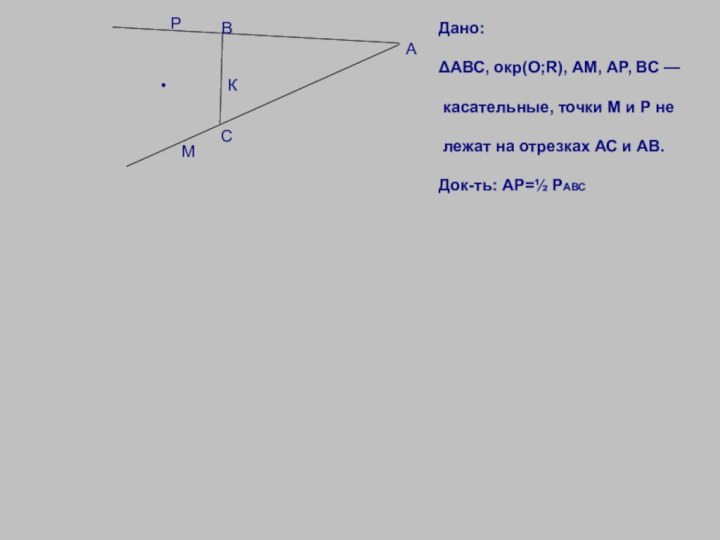
Дано:
ΔАВС, окр(О;R), АМ, АР, ВС —
касательные, точки М и Р не
лежат на отрезках
АС и АВ.Док-ть: АР=½ РАВС
Слайд 34
В
С
К
А
Р
М
•
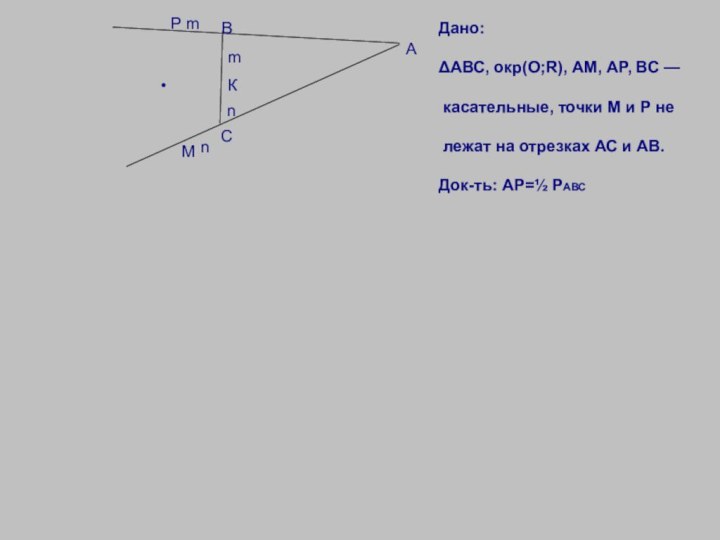
Дано:
ΔАВС, окр(О;R), АМ, АР, ВС —
касательные, точки М и Р не
лежат на отрезках
АС и АВ.Док-ть: АР=½ РАВС
m
m
n
n
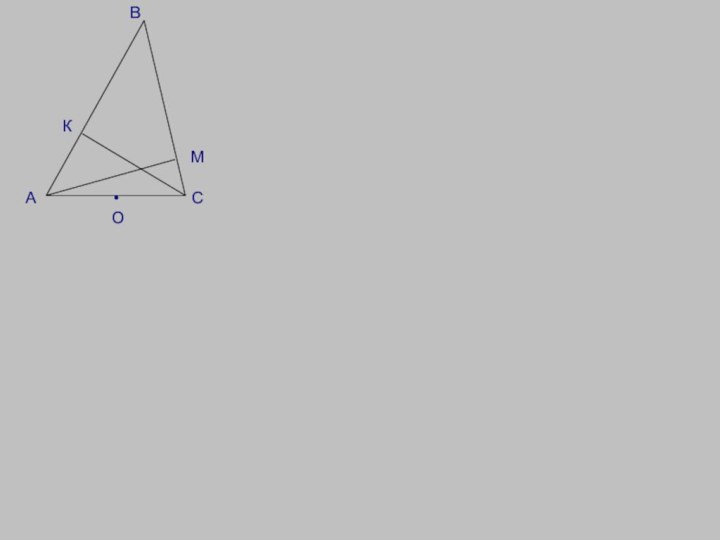
Слайд 35
В
С
К
А
Р
М
•
Дано:
ΔАВС, окр(О;R), АМ, АР, ВС —
касательные, точки М и Р не
лежат на отрезках
АС и АВ.Док-ть: АР=½ РАВС
Док-во.
1) Отрезки касательных, проведенных из одной точки, равны:
АР=АМ, ВР=ВК=m, СМ=СК=n
m
m
n
n
Слайд 36
В
С
К
А
Р
М
•
Дано:
ΔАВС, окр(О;R), АМ, АР, ВС —
касательные, точки М и Р не
лежат на отрезках
АС и АВ.Док-ть: АР=½ РАВС
Док-во.
1) Отрезки касательных, проведенных из одной точки, равны:
АР=АМ, ВР=ВК=m, СМ=СК=n
2) 2АР=АР+АМ=АВ+m+AC+n= AB+AC+(m+n)= АВ+АС+ВС
2АР=РАВС => АР=½ РАВС
m
m
n
n
Слайд 38
Чтобы решить задачу надо:
прочитав внимательно задачу несколько раз,
хорошо понять ее условие;
самостоятельно выполнить чертеж (аккуратный и достаточно
крупный);записать условие задачи;
вспомнить теорию по данной теме;
решить задачу, опираясь на теорию.