Слайд 2
Содержание
Цилиндр
Конус
Сфера
Исторические факты
Это интересно
Авторы
Слайд 3
Цилиндр
Цилиндр- тело, ограниченное цилиндрической поверхностью и двумя кругами
с границами.
Боковая поверхность- цилиндрическая поверхность
Основание- круги
Образующие-Образующие цилиндрической поверхности
Ось-прямая ОО1
Радиус-радиус
основания
Высота-длина образующей
Слайд 4
Виды сечений:
Осевое
Если секущая плоскость проходит через ось цилиндра
,то сечение представляет собой прямоугольник ,две стороны которого образующие,
а две другие- диаметры оснований цилиндра
Круговое
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон
Слайд 5
Площадь поверхности цилиндра
Площадью полной поверхности цилиндра называется сумма
площадей боковой поверхности и двух оснований. S=2πr(r+h)
Площадь боковой поверхности
цилиндра равна произведению длины окружности основания на высоту цилиндра.
За площадь боковой поверхности цилиндра принимается площадь ее развертки. S=2πrh
Слайд 6
Историческая справка про цилиндр
ЦИЛИНДР..
Слово "цилиндр" происходит от
греческого kylindros, что означает "валик", "каток".
Слайд 7
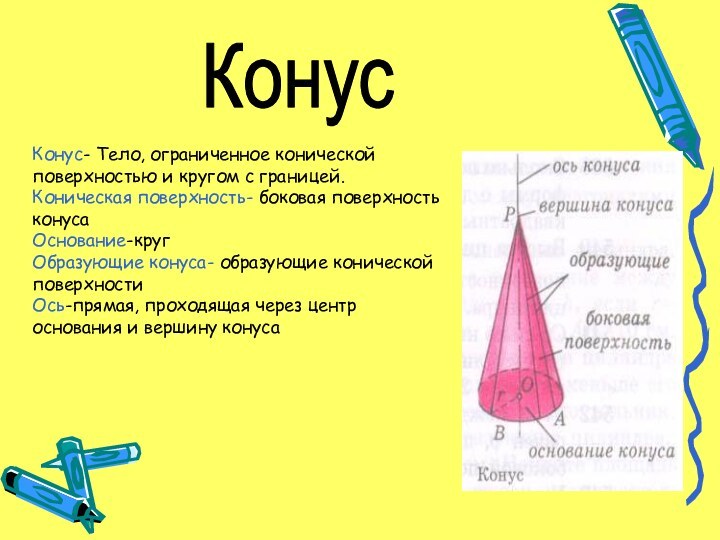
Конус
Конус- Тело, ограниченное конической поверхностью и кругом с
границей.
Коническая поверхность- боковая поверхность конуса
Основание-круг
Образующие конуса- образующие конической поверхности
Ось-прямая,
проходящая через центр основания и вершину конуса
Слайд 8
Виды сечений:
Осевое- Если секущая плоскость проходит через ось
конуса, то сечение представляет собой равнобедренный треугольник. Основание которого-диаметр
основания конуса, а боковые стороны-образующие конуса
Круговое- Если секущая плоскость перпендикулярна к оси конуса, то сечение является кругом
Конус может быть получен вращением прямоугольного треугольника вокруг одного из катетов.
Слайд 9
Площадь поверхности конуса
Площадь полной поверхности конуса называется сумма
площадей боковой поверхности и основанияS=πr(l+r)
Площадь боковой поверхности конуса равна
произведению половины длины окружности основания на образующую. S=πrl
За площадь боковой поверхности конуса принимается площадь ее развертки.
Слайд 11
Историческая справка про конус
ЦИЛИНДР.. Слово "цилиндр" происходит от
греческого kylindros, что означает "валик", "каток". КОНУС.
Латинское слово
conus заимствовано из греческого языка (konos - затычка, втулка, сосновая шишка). В XI книге "Начал" даётся следующее определение: если вращающийся около одного из своих катетов прямоугольный треугольник снова вернётся в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом. Евклид рассматривает только
Слайд 12
Сфера
Сфера- Поверхность, состоящая из всех точек пространства, расположенных
на данном расстоянии от данной точки.
Радиус-отрезок, соединяющий центр с
любой точкой сферы
Диаметр-отрезок, соединяющий две точки сферы и проходящий через ее центр.
Хорда-отрезок соединяющий любые две точки сферы.
Слайд 13
Площадь сферы
За площадь сферы примем предел последовательности площадей
поверхностей описанных около сферы многогранников при стремлении к нулю
наибольшего размера каждой грани. S=4πR^2
Слайд 14
Касательная плоскость к сфере
Касательная плоскость к сфере- плоскость,
имеющая со сферой только одну общую точку.
Точка касания- их
общая точка
Теорема:Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема:Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере
Слайд 15
Историческая справка про сферу
Однако оба слова "шар" и

"сфера" происходят от одного и того же греческого слова
"сфайра" - мяч. При этом слово "шар" образовалось от перехода согласных сф в ш. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы. Пифагорейцы учили о существовании десяти сфер Вселенной, по которым якобы двигаются небесные тела. Они утверждали, что расстояния этих тел друг от друга пропорциональны интервалам музыкальной гаммы. В этом усматривали элементы мировой гармонии. В подобных полумистических рассуждениях заключалась пифагорова "музыка сфер". Аристотель считал, что шарообразная форма, как наиболее совершенная, свойственна Луне, Солнцу, Земле и всем мировым телам. Развивая взгляды Евдокса, он полагал, что Земля окружена рядом концентрических сфер. Сфера всегда широко применялась в различных областях науки и техники. В XI книге "Начал" Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом.
Слайд 16
Это интересно
Водовзводная башня
Водовзводная башня была построена в
1488 году. Прежнее название башни - Свиблова - связано
с располагавшимся рядом двором боярина Свиблова. В 1633 году в башне была устроена водонапор-ная машина для перекачки воды в резервуар, расположенный на верху башни. Через трубы вода расходилась по всему Кремлю. В 1805-1806 годах башня была разобрана и сложена вновь по проекту архитектора И.В.Еготова. В 1812 году башня была взорвана французами, а в 1819 году восстановлена под руководством О.И.Бове. Высота башни до звезды - 57,7 метра, со звездой - 61,25 метра. Башня представляет собой цилиндр. В разрезе башня круглая.
Слайд 17
Кривоарбатский переулок, дом 10. Два огромных белых

цилиндра, прислоненных друг к другу. По периметру - шестьдесят
небольших ромбовидных окон, создающих образ улья. На фасаде - гигантское, в несколько метров окно. Над окном надпись: "Константин Мельников. Архитектор". Самая знаменитая (даже культовая) постройка 20-х годов в Москве. Константин Степанович Мельников родился в Москве в семье рабочего-строителя, выходца из крестьян, в 1890 г. Окончив приходскую школу, он работал "мальчиком" в фирме "Торговый дом Залесский и Чаплин". Чаплин помог ему поступить в 1905г. B Московское училище живописи, ваяния и зодчества, а затем после окончания Мельниковым в 1913г. живописного отделения посоветовал продолжить обучение на Архитектурном отделении, которое Константин Степанович окончил в 1917г. На старших курсах Училища и в первые годы после его окончания Мельников работает в духе неоклассики. Однако уже в начале 20-х годов Константин Степанович резко порывает с различного рода традиционалистскими стилизациями. Сам факт широкой реализации его произведений заставляет по-иному отнестись и к тем его произведениям, которые остались в проектах и которые в 20-е годы в острой полемике того периода нередко объявляли "фантастическими". В проектах Мельникова поражает степень раскованности творческой фантазии мастера в вопросах формообразования. Можно с полной уверенностью сказать, что в XX в. не было другого архитектора, который создал бы столько принципиально новых проектов и такого уровня новизны, что их оригинальность не только сильно оторвала их от работ других мастеров, но и столь же сильно отличала и от работ самого их автора.
Слайд 18
Пизанская башня
Пизанскую башню начали строить в 1174
году. Она задумывалась как колокольня расположенного рядом Домского собора.
Уже во время строительства, в 1298 году, выяснилось, что фундамент сооружения заложили криво. Кроме того, оказалось, что протекающая неподалеку подземная река смещает почвенные пласты и усиливает падение здания. Чтобы уменьшить скорость падения, архитекторы предложили изменить наклон её верней части. В результате к 1350 году, когда колокольню наконец достроили, она получилась не только наклонной, но и кривой. Однако падать Пизанская башня не перестала - к 1550 году отклонение её вершины от вертикали достигло уже 3,8 метра. После этого процесс падения несколько замедлился, однако к концу XX века вершина башни отклонилась от своего нормального положения уже на 4,7 метра.
Слайд 19
Гигантский шар в игрушечном городе
Это - космический
корабль "Земля", расположенный на окраине ДИСНЕЙЛЕНДА в штате Флорида.
По задумке эта сферическая конструкция должна олицетворять будущее человечества.
Слайд 20
Обман зрения в Праге
Так в Праге оформили
вход на станцию "Малостранска". Кольца соединены таким образом, что
создаётся иллюзия того, что мы видим сферу хотя на самом деле, кольца лежат в одной плоскости.
Слайд 21
Авторы
Демчишина Анна
Вечера Валентина