Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Сфера

Содержание

Примеры сферы:
СФЕРА Примеры сферы: Земля. Шар для игры в гольф. Определение сферыСферой называется поверхность, состоящая из всех точек пространства, расположенных на данном Как изобразить сферу?1. Отметить центр сферы (т.О)2. Начертить окружность с центром в Уравнение сферыЗададим прямоугольную систему координат ОxyzzхуМ(х;у;z)RC(x0;y0;z0)Построим сферу c центром в т. С Задача 1. Зная координаты центра С(2;-3;0) и радиус сферы R=5, записать уравнение сферы. Решение: так как уравнение сферы с радиусом R и центром Взаимное расположение сферы и плоскостиВведем прямоугольную систему координат OxyzПостроим плоскость α, совпадающую Взаимное расположение сферы и плоскостиrМРассмотрим 1 случай:d < R, т.е. если расстояние Взаимное расположение сферы и плоскостиРассмотрим 2 случай:d = R, т.е. если расстояние Взаимное расположение сферы и плоскостиРассмотрим 3 случай:d > R, т.е. если расстояние Площадь сферыСферу нельзя развернуть на плоскость.Опишем около сферы многогранник, так чтобы сфера Задача 2. Найти площадь поверхности сферы, радиус которой равен 6 см. Дано: сфера R = 6 смНайти: Sсф = ?Решение:Sсф = 4πR2Sсф =
Слайды презентации

Слайд 2 Примеры сферы:

Примеры сферы:

Слайд 3 Земля.

Земля.

Слайд 4 Шар для игры в гольф.

Шар для игры в гольф.

Слайд 5

Слайд 6

Слайд 7 Определение сферы
Сферой называется поверхность, состоящая из всех точек

Определение сферыСферой называется поверхность, состоящая из всех точек пространства, расположенных на


пространства, расположенных на данном расстоянии (R)
от данной точки

(центра т.О).

D

О

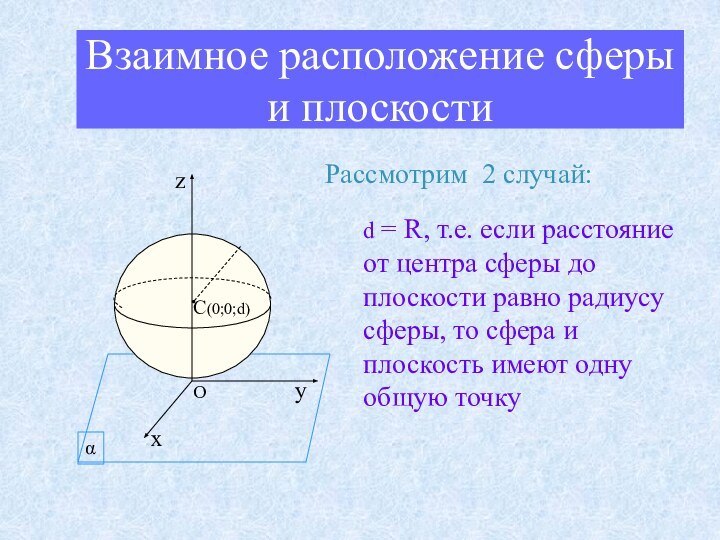
R – радиус сферы – отрезок,
соединяющий любую точку
сферы с центром.

D – диаметр сферы – отрезок,
соединяющий любые 2 точки
сферы и проходящий через центр.

т. О – центр сферы

Слайд 8 Как изобразить сферу?
1. Отметить центр сферы (т.О)
2. Начертить

Как изобразить сферу?1. Отметить центр сферы (т.О)2. Начертить окружность с центром

окружность с
центром в т.О
3. Изобразить видимую
вертикальную дугу
4.

Изобразить невидимую
вертикальную дугу

R

О

Изобразить видимую
горизонтальную дугу
6. Изобразить невидимую
горизонтальную дугу
7. Провести радиус сферы R

Слайд 9 Уравнение сферы
Зададим прямоугольную систему координат Оxyz
z
х
у
М(х;у;z)
R
C(x0;y0;z0)
Построим сферу c

Уравнение сферыЗададим прямоугольную систему координат ОxyzzхуМ(х;у;z)RC(x0;y0;z0)Построим сферу c центром в т.

центром в т. С и радиусом R
МС =

(x – x0)2 + (y – y0)2 + (z – z0)2

МС = R , или МС2 = R2

Следовательно, уравнение
сферы имеет вид:

(x – x0)2 + (y – y0)2 + (z – z0)2 = R2

Слайд 10 Задача 1. Зная координаты центра С(2;-3;0) и радиус сферы

Задача 1. Зная координаты центра С(2;-3;0) и радиус сферы R=5, записать уравнение сферы.

R=5, записать уравнение сферы.

Слайд 11 Решение:
так как уравнение сферы с

Решение: так как уравнение сферы с радиусом R и центром

радиусом R и центром в точке С(х0;у0;z0) имеет вид


(х-х0)2 + (у-у0)2 + (z-z0)2=R2, а координаты центра данной сферы С(2;-3;0) и радиус R=5, то уравнение данной сферы
(x-2)2 + (y+3)2 + z2=25

Ответ: (x-2)2 + (y+3)2 + z2=25

Слайд 12 Взаимное расположение сферы и плоскости
Введем прямоугольную систему координат

Взаимное расположение сферы и плоскостиВведем прямоугольную систему координат OxyzПостроим плоскость α,

Oxyz
Построим плоскость α, совпадающую с плоскостью Оху
Изобразим сферу с

центром в т.С, лежащей на положительной полуоси Oz и имеющей координаты (0;0;d), где d - расстояние (перпендикуляр) от центра сферы до плоскости α .

В зависимости от соотношения d и R возможны 3 случая…

Слайд 13 Взаимное расположение сферы и плоскости
r
М
Рассмотрим 1 случай:
d

Взаимное расположение сферы и плоскостиrМРассмотрим 1 случай:d < R, т.е. если

R, т.е. если расстояние от центра сферы до плоскости

меньше радиуса сферы, то сечение сферы плоскостью есть окружность радиусом r.

r = R2 - d2

Сечение шара плоскостью есть круг.

Слайд 14 Взаимное расположение сферы и плоскости
Рассмотрим 2 случай:
d =

Взаимное расположение сферы и плоскостиРассмотрим 2 случай:d = R, т.е. если

R, т.е. если расстояние от центра сферы до плоскости

равно радиусу сферы, то сфера и плоскость имеют одну общую точку

Слайд 15 Взаимное расположение сферы и плоскости
Рассмотрим 3 случай:
d >

Взаимное расположение сферы и плоскостиРассмотрим 3 случай:d > R, т.е. если

R, т.е. если расстояние от центра сферы до плоскости

больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Слайд 16 Площадь сферы
Сферу нельзя развернуть на плоскость.
Опишем около сферы

Площадь сферыСферу нельзя развернуть на плоскость.Опишем около сферы многогранник, так чтобы

многогранник, так чтобы сфера касалась всех его граней.
За площадь

сферы принимается предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани

Площадь сферы радиуса R: Sсф=4πR2

Sшара=4 Sкруга

т.е.: площадь поверхности шара равна учетверенной площади большего круга

Слайд 17 Задача 2. Найти площадь поверхности сферы, радиус которой равен

Задача 2. Найти площадь поверхности сферы, радиус которой равен 6 см.

6 см.

  • Имя файла: sfera.pptx
  • Количество просмотров: 175
  • Количество скачиваний: 0
- Предыдущая Дни воинской славы России
Следующая - Центры происхождения домашних животных

Похожие презентации

Конусы в нашей жизни Конусы в нашей жизни 172
Презентация по математике на тему Решение задач с помощью теоремы Пифагора Презентация по математике на тему Решение задач с помощью теоремы Пифагора 149
Нахождение суммы нескольких слагаемых Нахождение суммы нескольких слагаемых 167
ПЛОЩАДЬ ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ ПЛОЩАДЬ ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ 178
Цилиндр Цилиндр 134
Объём. Цилиндр, призма Объём. Цилиндр, призма 158
Формула Герона Формула Герона 209
9 класс Геометрия Презентация к уроку по геометрии Наложение 9 класс Геометрия Презентация к уроку по геометрии Наложение 161
Площади фигур Площади фигур 155
Двугранный угол Двугранный угол 174
Презентация по математике Решение геометрических задач при подготовке к ОГЭ Презентация по математике Решение геометрических задач при подготовке к ОГЭ 183
Квадрат Квадрат 142
Об углах между скрещивающимися прямыми Об углах между скрещивающимися прямыми 156
Презентация к уроку по теме Признаки параллельности прямых Презентация к уроку по теме Признаки параллельности прямых 151
Презентация по теме Начальные геометрические сведения Презентация по теме Начальные геометрические сведения 140
Окружность (7 класс) Окружность (7 класс) 190
Начальные понятия геометрии Начальные понятия геометрии 175
Тест по теме Усеченная пирамида Тест по теме Усеченная пирамида 308
Сущность и применение производной Сущность и применение производной 181
Методы решения тригонометрических уравнений Методы решения тригонометрических уравнений 146
Презентация по геометрии на темуГеометрические понятия и утверждения Презентация по геометрии на темуГеометрические понятия и утверждения 140
Теорема Пифагора Теорема Пифагора 152
Презентация урока геометрии в 10 классе по теме: Повторение. Углы и отрезки в окружности Презентация урока геометрии в 10 классе по теме: Повторение. Углы и отрезки в окружности 86
Практическая работа по теме треугольники Практическая работа по теме треугольники 225
Построение сечений Построение сечений 171
Изготовление набора для решения задач с пространственными телами Изготовление набора для решения задач с пространственными телами 155
Презентация Луч и угол Презентация Луч и угол 170
Параллелепипед Параллелепипед 171
Презентация к уроку Осевая симметрия Презентация к уроку Осевая симметрия 150
Решение задач на повторение Решение задач на повторение 179