- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему урока по геометрии на тему Признаки равенства прямоугольных треугольников
Содержание
- 2. Вопрос 1Какой треугольник называется прямоугольным? Ответ: Если один из углов треугольника прямой, то треугольник называется прямоугольным.1243
- 3. C B А ГипотенузаКатетКатетКак называются стороны прямоугольного треугольника?Вопрос 2
- 4. Назовите свойства прямоугольного треугольника.Вопрос 3Сумма острых углов
- 5. Решение задач по готовым чертежам
- 6. Решение задач по готовым чертежам1.Дано:
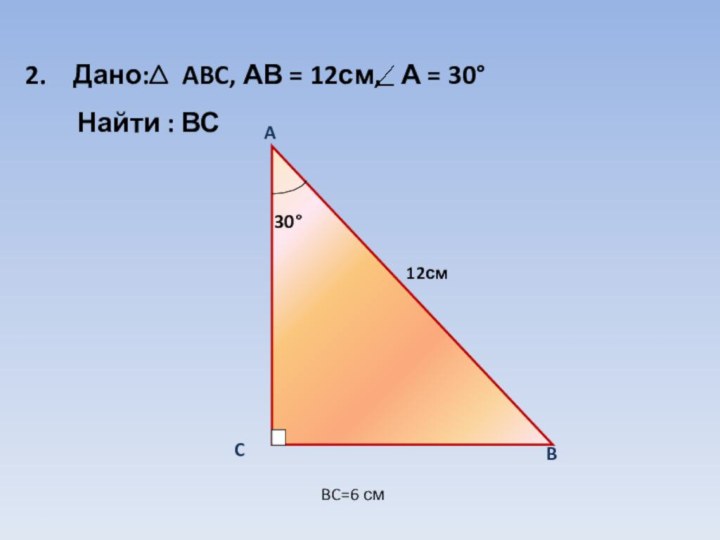
- 7. Дано: ABC, АВ = 12см,
- 8. 3. Дано:
- 9. A4,2см8,4смBC4. Дано: ABC, АВ = 4,2см, ВС = 8,4см. Найти:ВB=60
- 10. Признаки равенства прямоугольных треугольников.АCB А1 C1 B1
- 11. Решение задач с использованием признаковРавенства прямоугольных Треугольников.
- 12. Цели урока:научиться применять признаки равенства прямоугольных треугольников при решении типовых задач.
- 13. Задача 1АВСDДоказать: Δ АВD=Δ АСD
- 14. АВСDДоказать: Δ АВС=Δ АDСЗадача 2
- 15. АDВCДоказать: Δ АВD= Δ ВСDЗадача 3
- 16. Заполните пропуски в решении задачи.
- 17. № 261.
- 18. № 268. решить самостоятельно
- 19. Самопроверка.
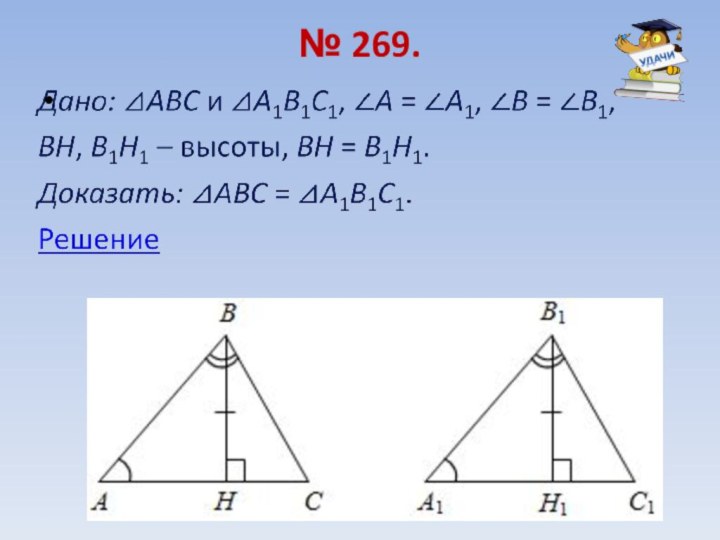
- 20. № 269.
- 21. Решите задачу.Докажите, что если треугольник прямоугольный,
- 22. Решите задачу.Дано: СМ = ВМ = МА.Доказать: ∆АВС – прямоугольныйРешение
- 23. Самостоятельная работа1. Дано: ∆ABC,BD – высота,
- 24. Самостоятельная работа Дано: ∆ABC,BD
- 25. Какой материал повторили на уроке?С какими трудностями
- 26. Домашнее задание:изучить п. 36; ответить на вопросы 12–13 на с. 88–89; решить задачи № 262, 264
- 27. Скачать презентацию
- 28. Похожие презентации























Слайд 2
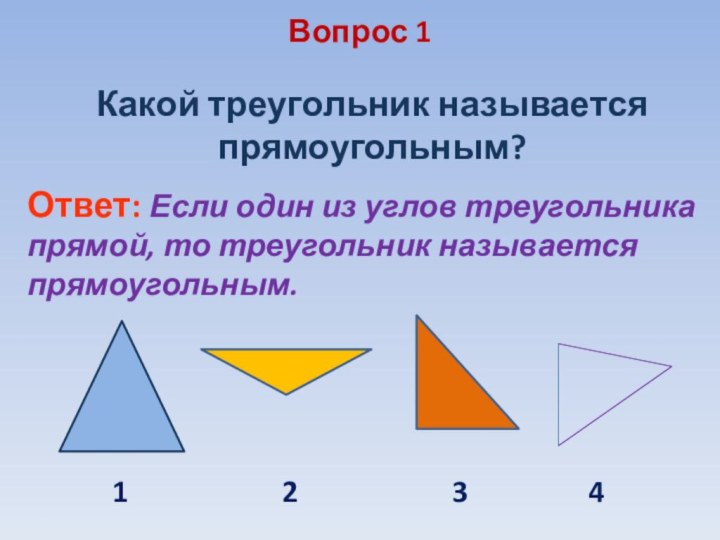
Вопрос 1
Какой треугольник называется прямоугольным?
Ответ: Если один
из углов треугольника прямой, то треугольник называется прямоугольным.
Слайд 4
Назовите свойства прямоугольного треугольника.
Вопрос 3
Сумма острых углов прямоугольного
треугольника равна 90°
Катет прямоугольного треугольника, лежащий против угла в
30° равен половине гипотенузы.Если катет равен половине гипотенузы то он лежит против угла в 30°.
Слайд 10
Признаки равенства прямоугольных треугольников.
А
C
B
А1
C1
B1
1.
=
2.
А
C
B
А1
C1
=
B1
Если катеты одного прямоугольного треугольника соответственно
равны катетам другого, то такие треугольники равны (по первому признаку равенства треугольников).Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны (по второму признаку равенства треугольников).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
А
C
B
А1
C1
B1
4.
3.
А1
C1
B1
=
=
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Слайд 12
Цели урока:
научиться применять признаки равенства прямоугольных треугольников при
решении типовых задач.
Слайд 21
Решите задачу.
Докажите, что если треугольник прямоугольный, то
медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
Решение
Слайд 23
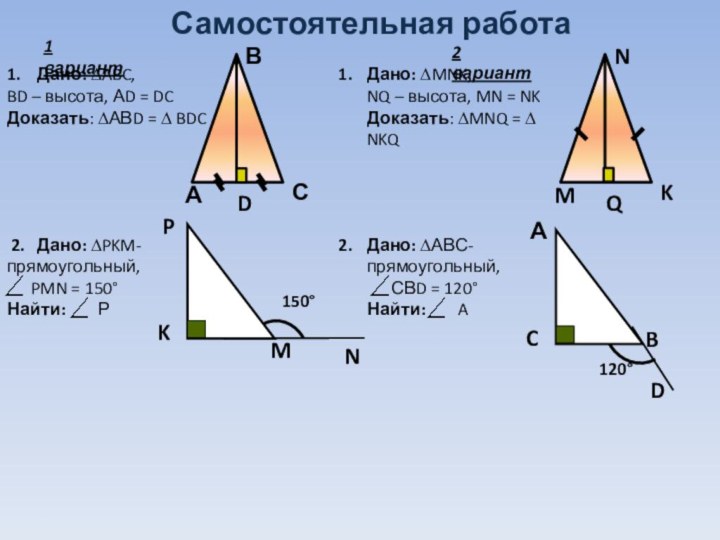
Самостоятельная работа
1. Дано: ∆ABC,
BD – высота, АD
= DC
Доказать: ∆АВD = ∆ BDC
Дано: ∆MNK,
NQ – высота,
MN = NKДоказать: ∆MNQ = ∆ NKQ
2. Дано: ∆PKM-прямоугольный,
PMN = 150
Найти: Р
Дано: ∆АВС-прямоугольный,
СВD = 120
Найти: A
1 вариант
2 вариант
1.
2.
Слайд 24
Самостоятельная работа
Дано: ∆ABC,
BD –
высота, АD = DC
Доказать: ∆АВD = ∆ BDC
Доказательство: АD
= DC по условию, BD – общая.Дано: ∆MNK,
NQ – высота, MN = NK
Доказать: ∆MNQ = ∆ NKQ
2. Дано: ∆PKM-прямоугольный,
PMN = 150
Найти: Р
Дано: ∆АВС-прямоугольный,
СВD = 120
Найти: A
∆АВD = ∆ BDC по
катетам.
1.
1.
2.
1 вариант
2 вариант
Доказательство:MN= NK по условию, NQ – общий катет.
∆MNQ = ∆ NKQ по гипотенузе и катету.
PMN = 180°-150 = 30°, как смежные углы.
Р = 90° - 30° = 60°, как сумма острых углов прямоугольного треугольника.
Ответ: 60°
Решение:
Решение:
АВС = 180°-120 = 60°,
как смежные углы.
А = 90° - 60° = 30°, как сумма острых углов прямоугольного треугольника.
Ответ: 30°
Слайд 25
Какой материал повторили на уроке?
С какими трудностями столкнулись?
Что необходимо повторить для успешной работы на
следующем уроке? Рефлексия.