фигур. Слово «геометрия» греческое, в переводе на русский
язык означает «землемерие».
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть























Основное свойство принадлежности точек и прямых на плоскости
А В
А
В
А
В
С
M N K
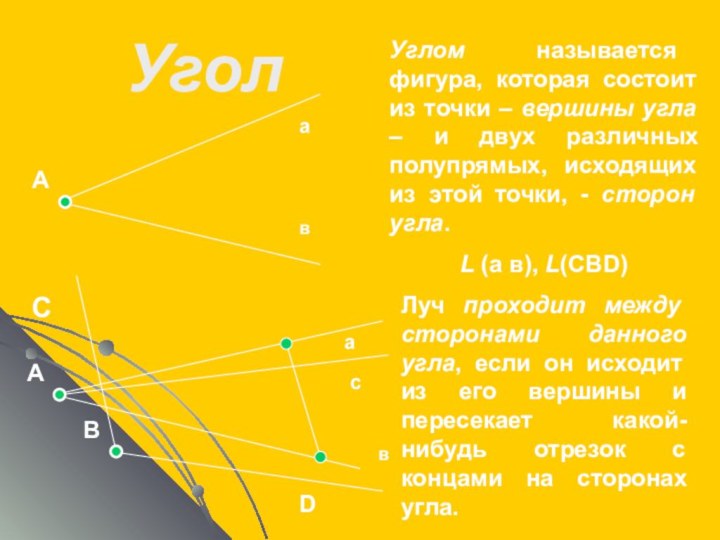
Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной ее точки
Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называют дополнительными.
А
а
в
с
Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.
Задача 1.
А
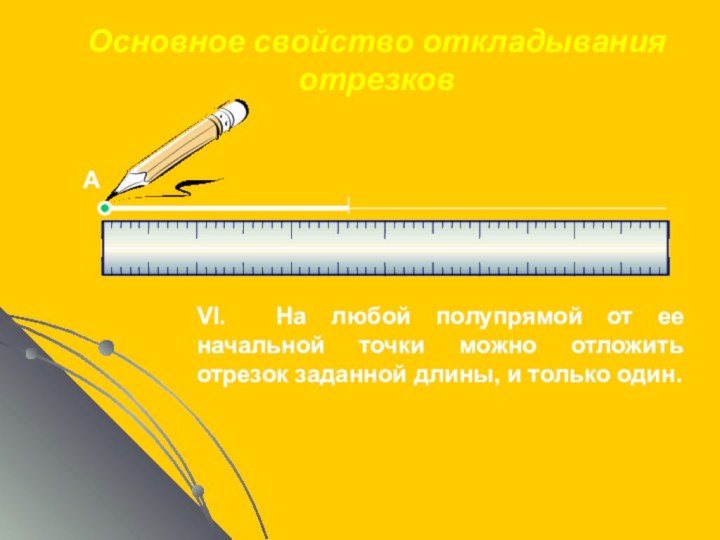
VII. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 1800 и только один.
А С
В
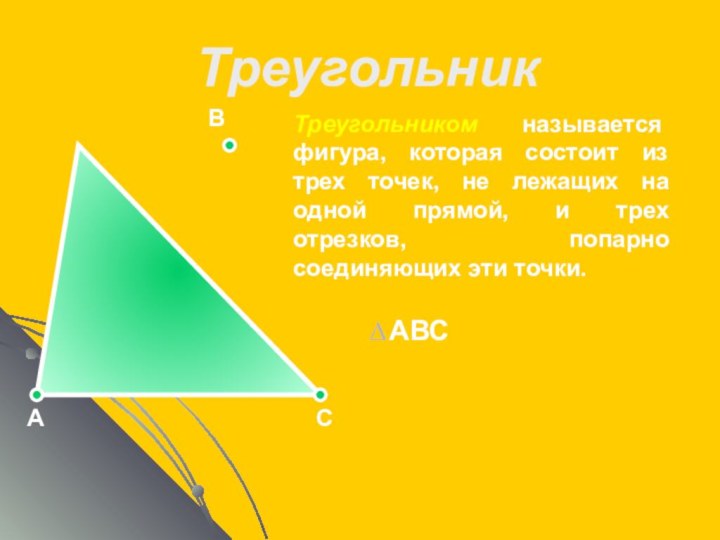
АВС
В1
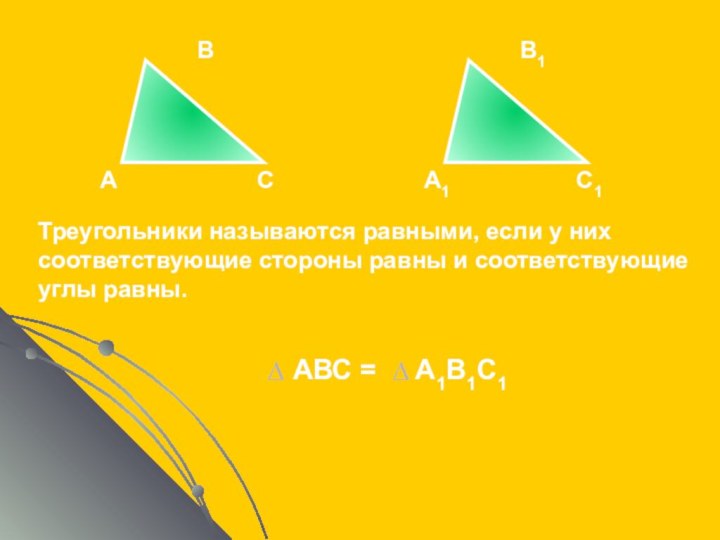
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны.
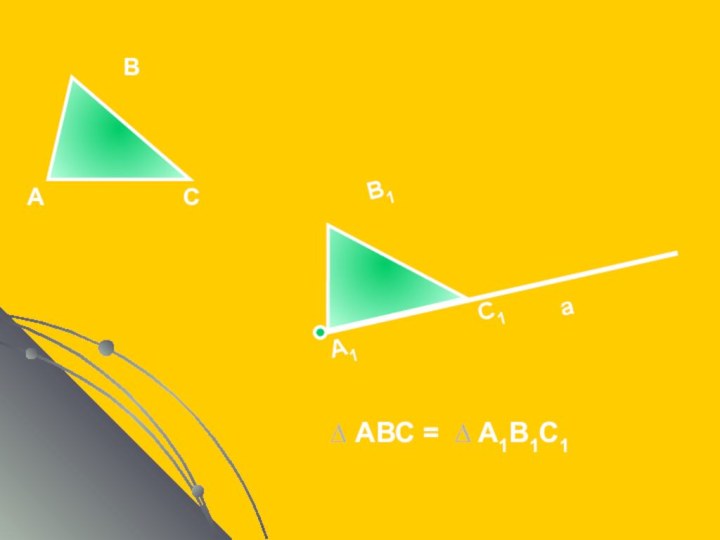
АВС = А1В1С1
Существование треугольника равного данному
Современной наукой установлено, что евклидова геометрия лишь приближенно, хотя и с очень большой точностью, описывает окружающее нас пространство, а в космических масштабах она имеет заметное отличие от геометрии реального пространства. Бурное развитие математики в XIX в привело к созданию выдающимся немецким математиком Б.Риманом (1826-1866 г.г) новой геометрии.