- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
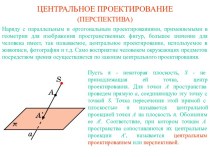
Презентация на тему по геометрии на тему: Признаки равенства треугольников (7 класс)
Содержание
- 2. Математический диктантВариант 1.1. Два угла, у которых
- 3. Математический диктантВариант 2.1. Два угла, у которых стороны одного угла являются продолжениями сторон другого, называются…
- 4. Математический диктантВариант 1.2. Сумма смежных углов равна…
- 5. Математический диктантВариант 2.2. Свойство вертикальных углов: вертикальные углы…
- 6. Математический диктантВариант 1.3. Треугольник, у которого две стороны равны, называется…
- 7. Математический диктантВариант 2.3. В равнобедренном треугольнике углы при основании …
- 8. Математический диктантВариант 1.4. В равнобедренном треугольнике биссектриса, проведенная к основанию, является…
- 9. Математический диктантВариант 2.4. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется…
- 10. Математический диктантВариант 1.5. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется…
- 11. Математический диктантВариант 2.5. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется…
- 12. Проверка математического диктантаВариант 1.1. Два угла, у
- 13. Признаки равенства треугольниковI признак равенства треугольниковΔABC =
- 14. Признаки равенства треугольниковII признак равенства треугольниковΔCDE =
- 15. Решение задачДано:Доказать:План.Задача №172AC = AD, AB⊥CDCB =BD,
- 16. Решение задачДано:Доказать:Задача №162(а)ADE-равнобедренный,AD = AE, DB = CEAB = AC, ∠CAD = ∠BAEADBCE
- 17. Тестовая работаАлгоритм работы с тестом1. Внимательно прочитай
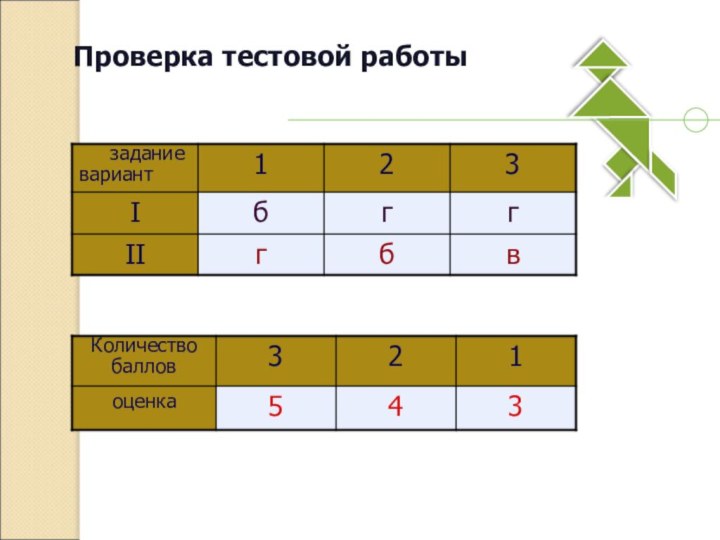
- 18. Проверка тестовой работы
- 19. Историческая справкаЕвклид (конец IV – III в.до
- 20. Историческая справкаЗадача Евклида1. Дан угол BAC.2. Возьмем
- 21. Домашнее заданиеЗавершить решение задачи Евклида. Доказать,
- 22. Скачать презентацию
- 23. Похожие презентации
Математический диктантВариант 1.1. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются…
















Слайд 3
Математический диктант
Вариант 2.
1. Два угла, у которых стороны
одного угла являются продолжениями сторон другого, называются…
Слайд 8
Математический диктант
Вариант 1.
4. В равнобедренном треугольнике биссектриса, проведенная
к основанию, является…
Слайд 9
Математический диктант
Вариант 2.
4. Отрезок, соединяющий вершину треугольника с
серединой противоположной стороны, называется…
Слайд 10
Математический диктант
Вариант 1.
5. Отрезок биссектрисы угла треугольника, соединяющий
вершину треугольника с точкой противоположной стороны,
называется…
Слайд 11
Математический диктант
Вариант 2.
5. Перпендикуляр, проведенный из вершины треугольника
к прямой, содержащей противоположную сторону, называется…
Слайд 12
Проверка математического диктанта
Вариант 1.
1. Два угла, у которых
одна сторона общая, а две другие являются продолжениями одна
другой, называютсясмежными.
2. Сумма смежных углов равна
180°.
3. Треугольник, у которого две стороны равны,
называется
равнобедренным.
4. В равнобедренном треугольнике биссектриса, проведенная к
основанию, является
медианой и высотой.
5. Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны,
называется
биссектрисой треугольника.
Слайд 13
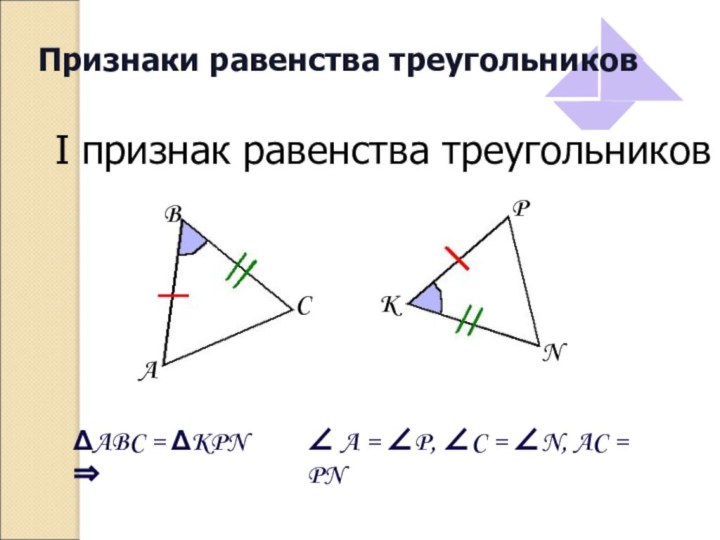
Признаки равенства треугольников
I признак равенства треугольников
ΔABC = ΔKPN
⇒
∠ A = ∠P, ∠C = ∠N, AC =
PNA
B
C
K
P
N
Слайд 14
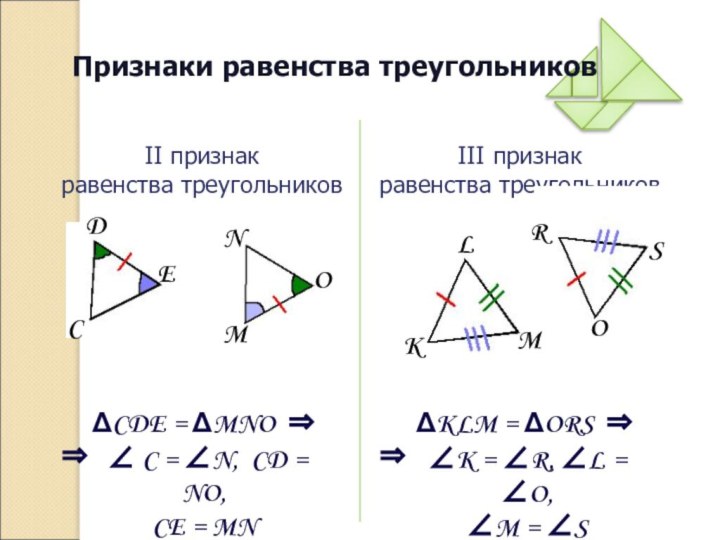
Признаки равенства треугольников
II признак
равенства треугольников
ΔCDE = ΔMNO
⇒
⇒
III признак
равенства треугольников
ΔKLM = ΔORS ⇒
⇒
∠ C = ∠N, CD = NO,CE = MN
∠K = ∠R, ∠L = ∠O,
∠M = ∠S
C
D
E
M
N
O
K
L
M
S
R
O
Слайд 15
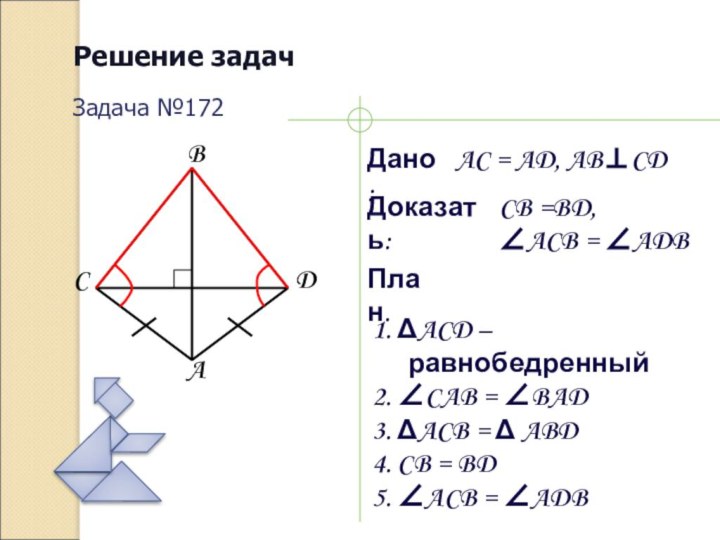
Решение задач
Дано:
Доказать:
План.
Задача №172
AC = AD, AB⊥CD
CB =BD,
∠ACB
= ∠ADB
1. ΔACD – равнобедренный
2. ∠CAB = ∠BAD
3. ΔACB
= Δ ABD4. CB = BD
5. ∠ACB = ∠ADB
A
B
D
C
Слайд 16
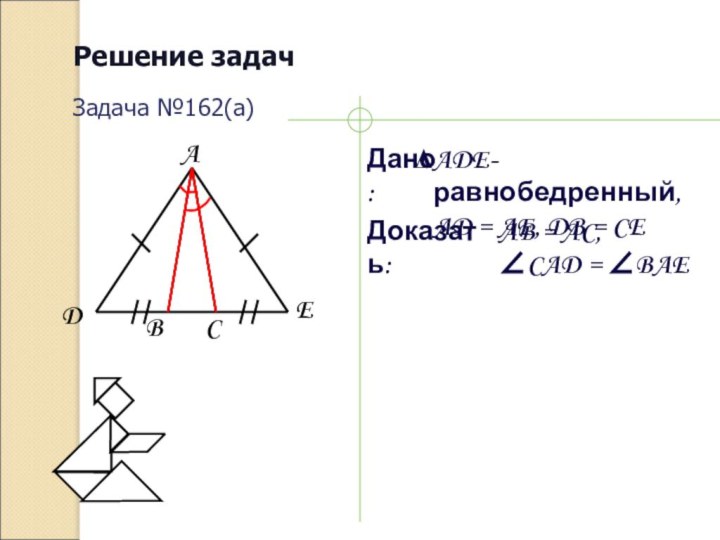
Решение задач
Дано:
Доказать:
Задача №162(а)
ADE-равнобедренный,
AD = AE, DB = CE
AB
= AC,
∠CAD = ∠BAE
A
D
B
C
E
Слайд 17
Тестовая работа
Алгоритм работы с тестом
1. Внимательно прочитай задачу.
2.
Реши задачу.
3. Из четырех предложенных ответов
выбери один правильный.
4.
Букву, соответствующую правильному ответу,
занеси в карточку ответов.5. Приступай к решению следующей задачи.
Слайд 19
Историческая справка
Евклид (конец IV – III в.до н.
э.)
Древнегреческий математик;
автор труда «Начала» в 13 книгах,
в котором
изложены основы
геометрии, теории чисел, метод
определения площадей и объемов;
оказал огромное влияние на
развитие математики.
Слайд 20
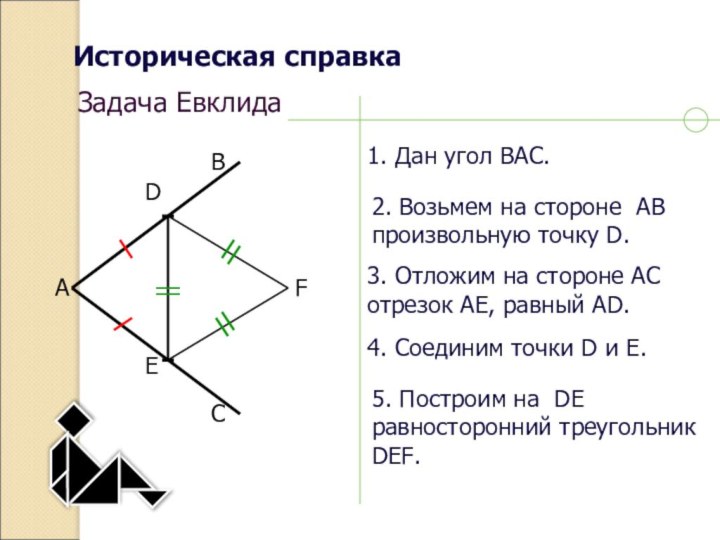
Историческая справка
Задача Евклида
1. Дан угол BAC.
2. Возьмем на
стороне AB
произвольную точку D.
3. Отложим на стороне AC
отрезок
AE, равный AD.4. Соединим точки D и E.
5. Построим на DE
равносторонний треугольник
DEF.
A
B
C
D
E
F
Слайд 21
Домашнее задание
Завершить решение задачи Евклида. Доказать,
что построенный
луч является биссектрисой угла BAC.
2. Подготовить ответы на вопросы
к главе II.