- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площадь
Содержание
- 2. СодержаниеЕдиница измеренияСвойства площадейПлощадь прямоугольникаПлощадь параллелограммаПлощадь треугольникаПлощадь трапецииТеорема ПифагораТеорема, обратная теореме Пифагора
- 3. Единица измеренияОсновная единица измерения – м2 (мм2,
- 4. Свойства площадейРавные многоугольники имеют равные площади.Если многоугольник
- 5. Площадь прямоугольникаДано: прямоугольник со сторонами a
- 6. Задача: Найти площадь прямоугольника со сторонами 4
- 7. Площадь параллелограмма Дано: параллелограмм ABCD.Доказать: S =
- 8. Задача: Найти площадь параллелограмма, если основание 8
- 9. Площадь треугольникаДано: ∆ABC, AB – основание, CH
- 10. Задача: Найти площадь треугольника с основанием 10
- 11. Площадь трапецииДано: трапеция ABCD; AD и BC
- 12. Задача: Найти площадь трапеции с основаниями 4
- 13. Теорема ПифагораДано: a, b, c – стороны
- 14. Задача: Найти гипотенузу прямоугольного треугольника с катетами
- 15. Скачать презентацию
- 16. Похожие презентации







Слайд 2
Содержание
Единица измерения
Свойства площадей
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Теорема,
обратная теореме Пифагора
Слайд 3
Единица измерения
Основная единица измерения – м2 (мм2, см2,
км2, ар, га)
1 см x 1 см = 1
см21 мм2 = 0,01 см2
1 см2 = 0,0001 м2
1 км2 = 1000000 м2
1 ар = 100 м2
1 гектар = 10000 м2
1 акр = 4046,8564224 м2
Назад
Слайд 4
Свойства площадей
Равные многоугольники имеют равные площади.
Если многоугольник составлен
из нескольких многоугольников, то его площадь равна сумме площадей
этих много- угольников.Площадь квадрата равна квадрату его стороны.
Назад
Слайд 5
Площадь прямоугольника
Дано: прямоугольник со
сторонами a и b.
Доказать:
S = ab.
Доказательство:
(a + b)2 = S + S
+ a2 + b2а2 + 2ab +b2 = 2S + a2 + b2
S = ab. Теорема доказана.
Назад
Теорема:
Площадь прямоугольника равна
произведению его смежных сторон.
Задача
Слайд 6 Задача: Найти площадь прямоугольника со сторонами 4 и
2.
Дано: прямоугольник со сторонами a и b,
a = 4
см, b = 2 см.Найти: S.
Решение:
S = ab
S = 4 см ∙ 2 см = 8 см2
Ответ: S = 8 см2
Назад
К теореме
Слайд 7
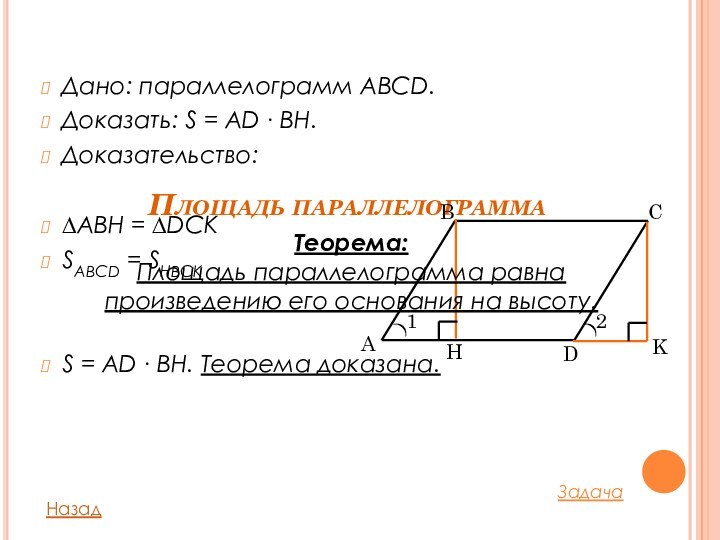
Площадь параллелограмма
Дано: параллелограмм ABCD.
Доказать: S = AD
∙ BH.
Доказательство:
∆ABH = ∆DCK
SABCD = SHBCK
S = AD ∙
BH. Теорема доказана.Назад
Теорема:
Площадь параллелограмма равна
произведению его основания на высоту.
Задача
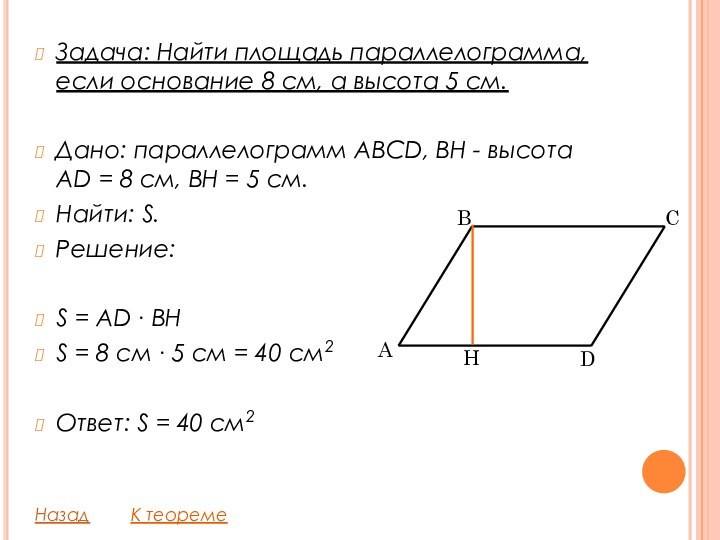
Слайд 8 Задача: Найти площадь параллелограмма, если основание 8 см,
а высота 5 см.
Дано: параллелограмм ABCD, BH - высота
AD
= 8 см, BH = 5 см.Найти: S.
Решение:
S = AD ∙ BH
S = 8 см ∙ 5 см = 40 см2
Ответ: S = 40 см2
Назад
К теореме
Слайд 9
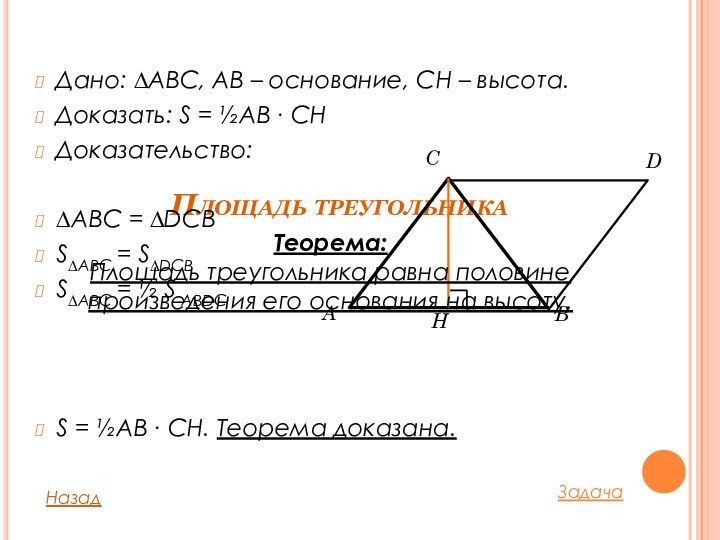
Площадь треугольника
Дано: ∆ABC, AB – основание, CH –
высота.
Доказать: S = ½AB ∙ CH
Доказательство:
∆ABC = ∆DCB
S∆ABC
= S∆DCBS∆ABC = ½ S ABDC
S = ½AB ∙ CH. Теорема доказана.
Назад
Теорема:
Площадь треугольника равна половине
произведения его основания на высоту.
Задача
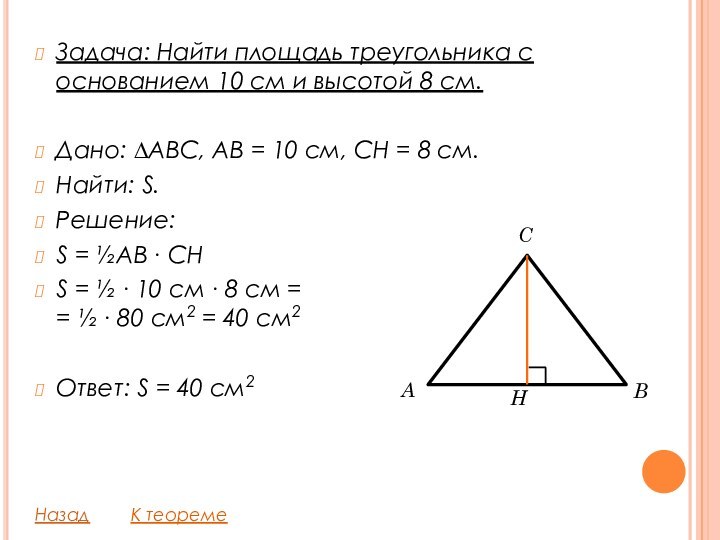
Слайд 10 Задача: Найти площадь треугольника с основанием 10 см
и высотой 8 см.
Дано: ∆ABC, AB = 10 см,
CH = 8 см. Найти: S.
Решение:
S = ½AB ∙ CH
S = ½ ∙ 10 см ∙ 8 см = = ½ ∙ 80 см2 = 40 см2
Ответ: S = 40 см2
Назад
К теореме
Слайд 11
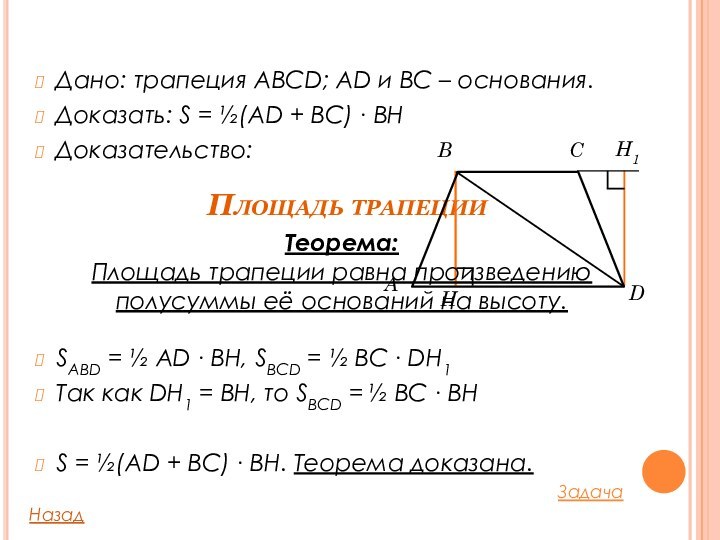
Площадь трапеции
Дано: трапеция ABCD; AD и BC –
основания.
Доказать: S = ½(AD + BC) ∙ BH
Доказательство:
SABD =
½ AD ∙ BH, SBCD = ½ BC ∙ DH1 Так как DH1 = BH, то SBCD = ½ BC ∙ BH
S = ½(AD + BC) ∙ BH. Теорема доказана.
Назад
Теорема:
Площадь трапеции равна произведению
полусуммы её оснований на высоту.
Задача
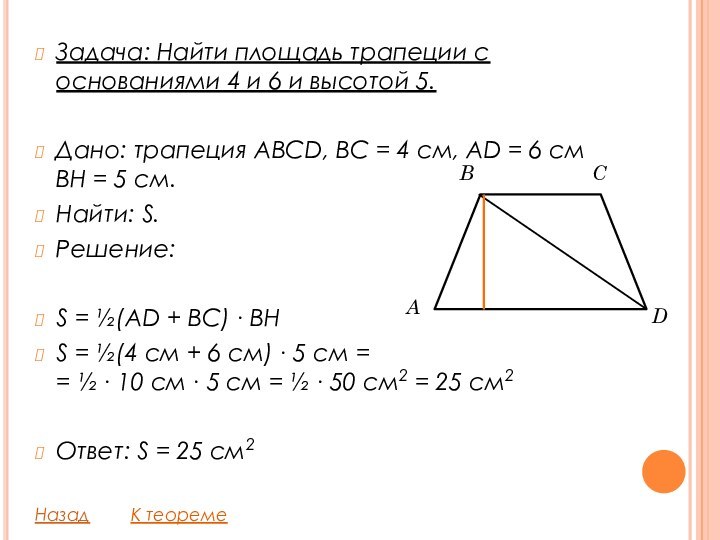
Слайд 12 Задача: Найти площадь трапеции с основаниями 4 и
6 и высотой 5.
Дано: трапеция ABCD, BC = 4
см, AD = 6 см
BH = 5 см.Найти: S.
Решение:
S = ½(AD + BC) ∙ BH
S = ½(4 см + 6 см) ∙ 5 см = = ½ ∙ 10 см ∙ 5 см = ½ ∙ 50 см2 = 25 см2
Ответ: S = 25 см2
Назад
К теореме
Слайд 13
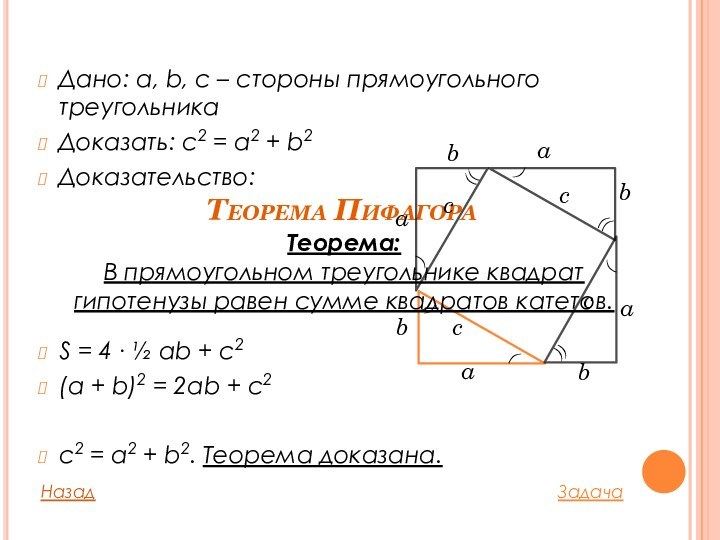
Теорема Пифагора
Дано: a, b, c – стороны прямоугольного
треугольника
Доказать: с2 = a2 + b2
Доказательство:
S = 4 ∙
½ ab + c2 (a + b)2 = 2ab + c2
с2 = a2 + b2. Теорема доказана.
Назад
Теорема:
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Задача
Слайд 14 Задача: Найти гипотенузу прямоугольного треугольника с катетами 4
и 3.
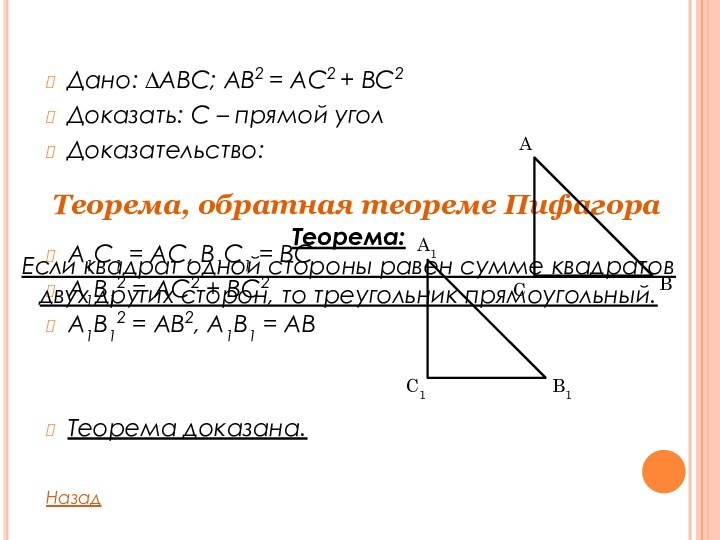
Дано: ∆ABC, AC = 3 см, BC =
4 см, C – прямой.Найти: AB.
Решение:
AB2 = AC2 + BC2
AB2 = 32 + 42 = 9 + 16 = 25
AB = = 5
Ответ: AB = 5 см
Назад
К теореме