Слайд 2
Цели урока
Систематизировать знания о сторонах, углах, вершинах, о
площади треугольника и обобщить эти знания для доказательства теоремы
Пифагора.
Формировать умения применять ранее полученные знания о треугольниках, для получения новых знаний.
Р азвивать математическое мышление.
Формировать учебно-интеллектуальные умения: анализировать, обобщать, сравнивать; коммуникативные умения.
Воспитывать интерес к математике.
Слайд 3
“Геометрия владеет двумя сокровищами: одно из них -
это теорема Пифагора, а другое - деление отрезка в
среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень”.
Иоганн Кеплер
Слайд 4
Хронология развития
теоремы до Пифагора:
Пифагор родился на острове Самос,
расположенном в Эгейском море.
Четыре года подряд был
олимпийским чемпионом .
По совету Фалеса 22 года Пифагор
набирался мудрости в Египте.
Во время завоевательных походов
попал в плен, был продан в рабство
и 10 лет жил в Вавилоне.
Вернувшись на Родину, Пифагор организовал
Пифагорейский орден – школу философов и математиков. Во время народного восстания в 496 г.
до нашей эры был убит в уличной схватке.
Слайд 8
Теорема Пифагора – важнейшее утверждение геометрии.
Даже те, кто в своей жизни навсегда «распрощался» с
математикой, сохраняют воспоминания о «пифагоровых штанах». Причина такой популярности теоремы Пифагора объясняется её простотой, красотой, значимостью.
Слайд 9
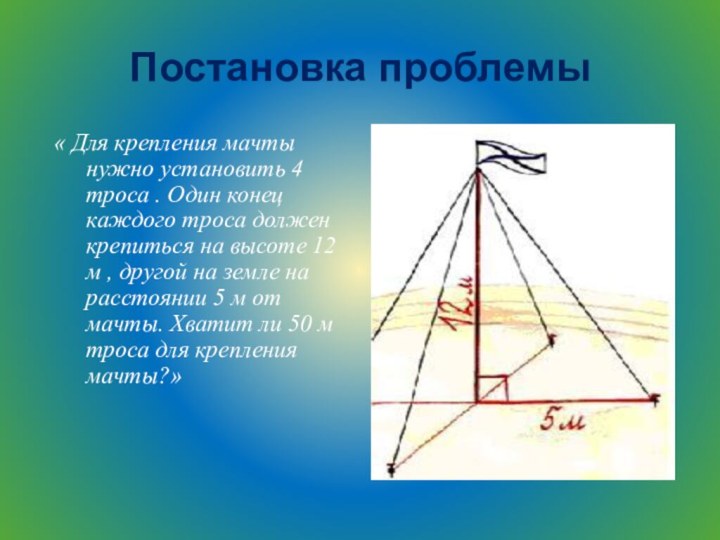
Постановка проблемы
« Для крепления мачты нужно установить 4
троса . Один конец каждого троса должен крепиться на
высоте 12 м , другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?»
Слайд 10
ГИПОТЕНУЗА
КАТЕТ
КАТЕТ
Это прямоугольный треугольник
Слайд 11
Современная формулировка
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов.
Слайд 12
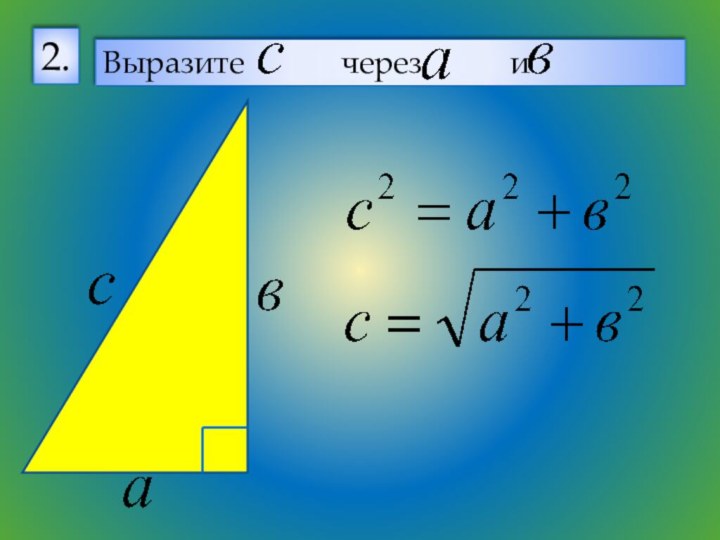
Дано:
прямоугольный
треугольник,
- катеты,
- гипотенуза
Доказать:
Слайд 15
.
Если дан нам треугольник
И притом с прямым
углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму
степеней находим —
И таким простым путем
К результату мы придём.
Слайд 16
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме
квадратов, построенных на его катетах.
Слайд 17
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме
квадратов, построенных на его катетах.
Почтовая марка
по случаю переименования острова Самос в остров Пифагорейон. На марке надпись: « т.Пифагора. Эллас. 350 драхи».
Слайд 18
Дано:
∆АВС – прямоугольный
а = ВС –
катет
в = АС – катет,
с = АВ – гипотенуза.
A
B
C
с
S = c2
в
S = в2
a
S = a2
Док-ть: с2 = а2 + в2
или
АВ2 = АС2 + ВС2
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах...
Док-во:
Слайд 19
Эпилог.
Вечный кладезь
мудрости.
Слайд 20
Учение Пифагора не погибло в кротонском
пожаре. Подобранные горсткой оставшихся в живых учеников зерна этого
учения не только были сохранены, но и дали обильные всходы. Благодарная память единомышленников сохранила для человечества имя Пифагора — выдающегося математического гения, творца акустики, основоположника теории музыки, «Коперника древней астрономии», основателя религиозного братства — прообраза средневековых монашеских орденов, богослова и реформатора, человека высокой нравственности, личности богатой, противоречивой и загадочной, стоящей на рубеже пробуждающейся науки и пышно цветущей мифологии.
Слайд 21
И чем дальше неумолимое время уносит
нас от времени Пифагора, тем острее видится поразительная прозорливость
эллинского мудреца, объявившего два с половиной тысячелетия назад, что «Всё есть число». Если снять с этого тезиса мистическую паутину, то нам откроется гениальное пророчество, определившее весь последующий путь развития науки. Тогда древний пифагорейский тезис примет современное звучание: математика есть ключ к познанию всех тайн природы.
Слайд 22
Именно так определяет роль Пифагора
в истории естествознания современный американский математик и историк науки
М. Клайн: «Но то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило всё последующее развитие науки: во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики; во-вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы».
Слайд 23
В Абдерах в 430—420-х гг. до
н. э. (т. е. менее чем через 100 лет
после смерти Пифагора) произошло невиданное событие: в Абдерах были выпущены монеты с изображением Пифагора и подписью. Абдерские монеты — это не только первый в истории чеканный портрет философа, но это и первое на греческих монетах подписанное изображение человека. И таким человеком оказался не царь, не тиран, не полководец, а мудрец! Что касается Пифагора-математика, то он, видимо, навсегда останется первым и последним математиком в истории человечества, чей профиль удостоился столь высокой чести!
Слайд 24
Самосская монета с изображением Пифагора. II-III
вв. Прорисовка. Конечно, это не портрет Пифагора, а обобщённый
образ учёного.
Слайд 25
Но для учёного важнее не
внешние атрибуты славы, а признание и дальнейшая жизнь его
идей. И здесь Пифагору также светила счастливая звезда. Идеями Пифагора пронизано творчество Платона — величайшего философа в истории человечества. Плотин, Порфирий, Ямвлих, Прокл, первая женщина философ и математик Гипатия, растерзанная толпой фанатиков-христиан,— все они были страстными приверженцами Пифагора. Неоплатонизм, уходящий корнями в древнее пифагорейство, стал мощным философским течением, идущим из античности в современность. Идеи неоплатоников питали Аврелия Августина (354—430) и Иоанна Скота Эриугену (810—877), Николая Кузанского (1401 —1464) и Джероламо Кардано (1501 —1576), Томмазо Кампанеллу (1568—1639) и Джордано Бруно (1548—1600), Фридриха Шеллинга (1775— 1854) и Георга Гегеля (1770—1831), Владимира Соловьева (1853—1900) и Сергея Булгакова (1871 —1944), Павла Флоренского (1882—1937?) и Алексея Лосева (1893—1988).
Слайд 26
Заложенная Пифагором вера в красоту и
гармонию природы, в мудрую простоту и целесообразность её законов,
построенных на единых математических принципах, окрыляла творчество титанов современного естествознания от Иоганна Кеплера (1571 —1630) до Альберта Эйнштейна (1879—1955). Это и есть путеводная звезда современного естествознания, тот вечный кладезь мудрости, который открыл человечеству Пифагор.
Слайд 27
“Геометрия владеет двумя сокровищами: одно из них -
это теорема Пифагора, а другое - деление отрезка в
среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень”.
Иоганн Кеплер
Слайд 28
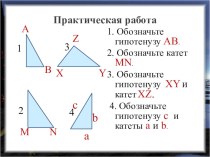
1.
Запишите теорему Пифагора для каждого треугольника
А
В
С
О
N
M
X
Y
Z
Треугольник не прямоугольный
F
K
S
Слайд 33
Темы сообщений
Различные формулировки теоремы Пифагора.
Различные доказательства теоремы Пифагора.
Практические
задачи, решаемые с помощью теоремы Пифагора.
Пифагор в литературе. Легенды
о Пифагоре.