Презентация на тему Треугольники

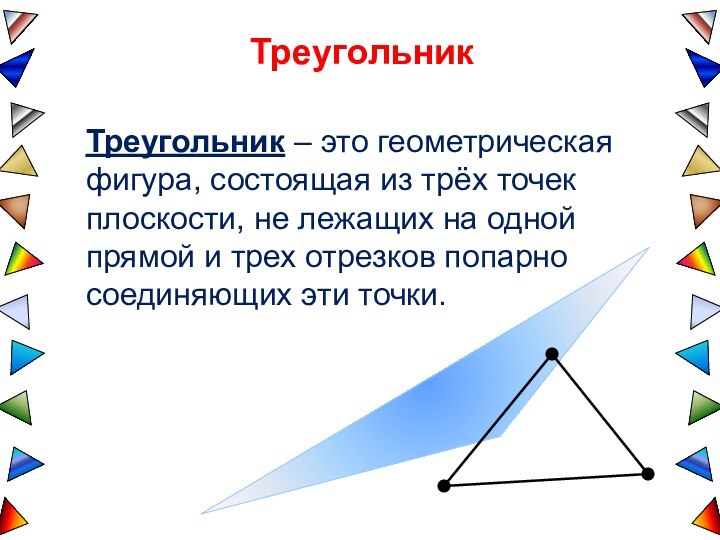
точек плоскости, не лежащих на одной прямой и трех

стороны, называется медианой треугольника

треугольника с точкой противоположной стороны, называется

содержащей противоположную сторону, называется
высотой треугольника.

если все его стороны равны

треугольнике углы при основании равны
Теорема. В

угол между ними одного треугольника соответственно равны двум сторонам

прилежащих к ней угла одного треугольника соответственно равны стороне

треугольника соответственно равны трём сторонам другого треугольника, то такие

из линий треугольника всегда лежат внутри треугольника?

Какие из линий

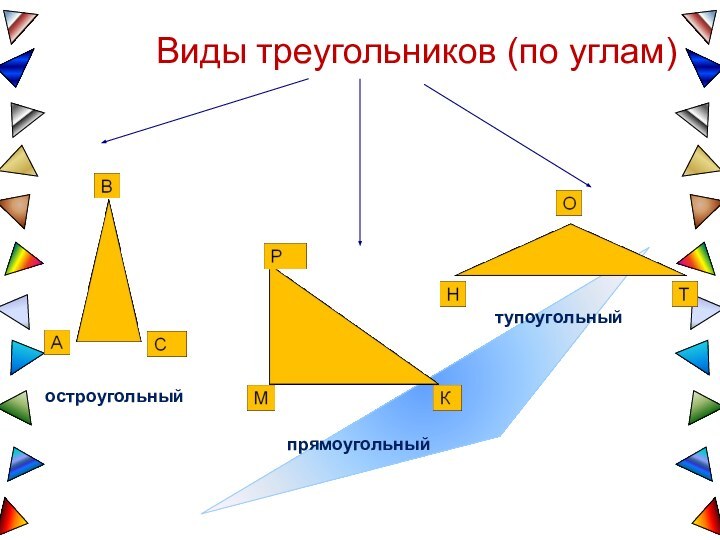
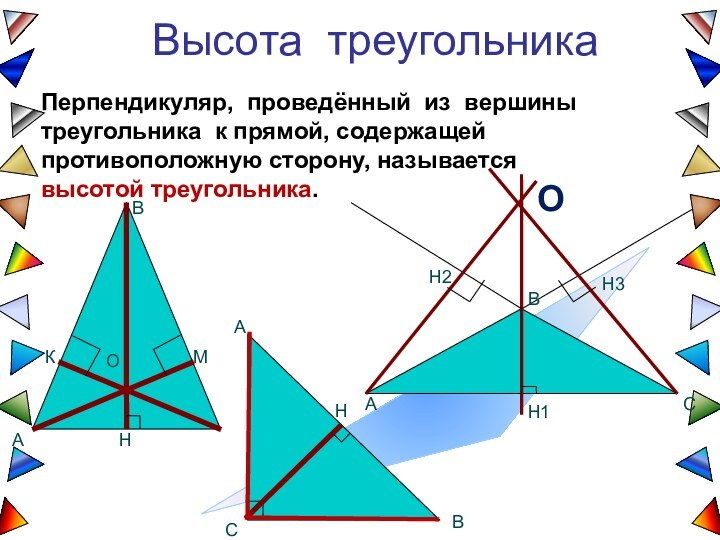
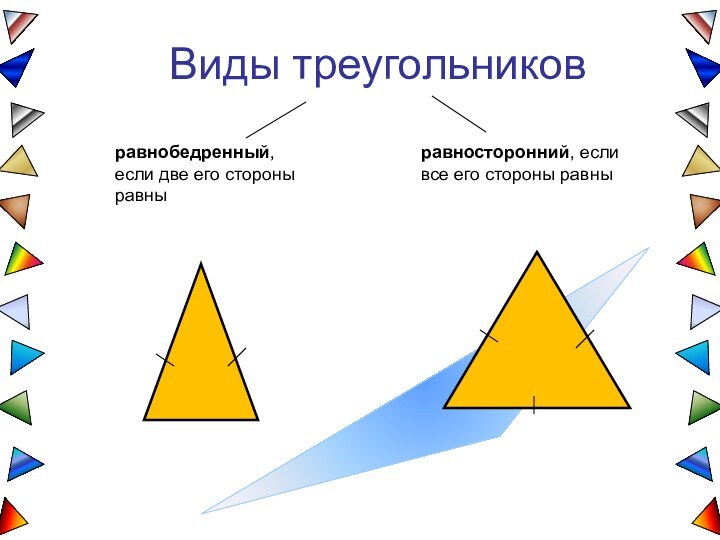
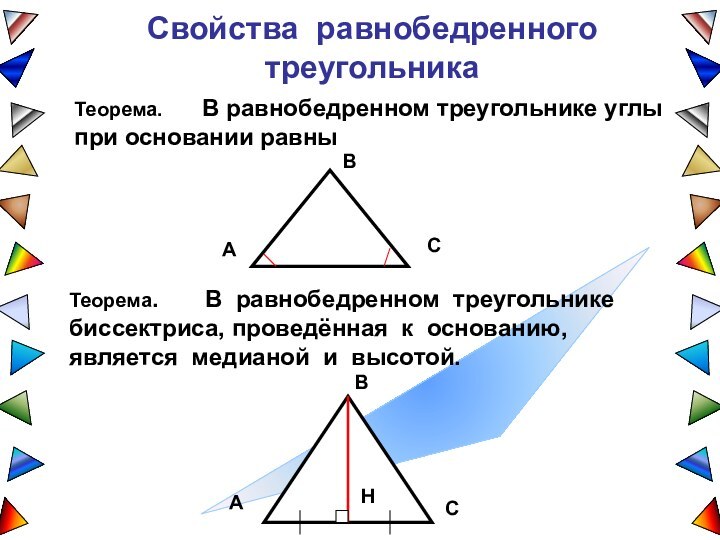
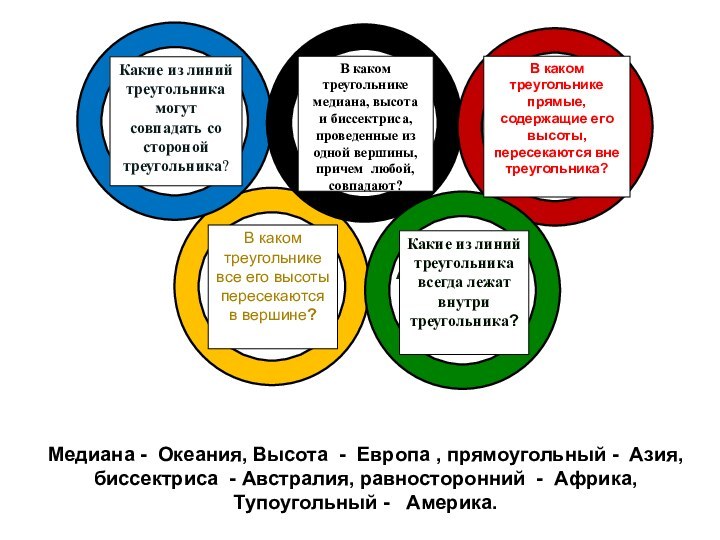
В каком треугольнике медиана, высота и биссектриса, проведенные из одной вершины, причем любой, совпадают?

В каком треугольнике прямые, содержащие его высоты, пересекаются вне треугольника?

В каком треугольнике все его высоты пересекаются в вершине?

Медиана - Океания, Высота - Европа , прямоугольный - Азия,
биссектриса - Австралия, равносторонний - Африка,
Тупоугольный - Америка.

честной спортивной борьбы.
« Быстрее, выше, сильнее! »
«По 1

двум углам, на которые медиана разбивает угол треугольника.
Дано: BM=B1M1,

B1M1=M1D1.
1.ΔAMD= ΔCMB, ΔA1M1D1= ΔC1M1B1 (1 признак)

равенства этих треугольников следуют равенства: AD=BC, A1D1=B1C1 и

3. ΔABC=

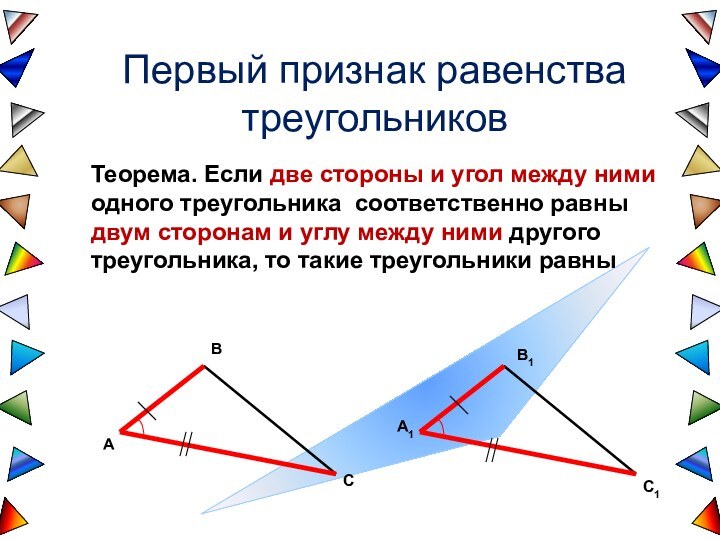
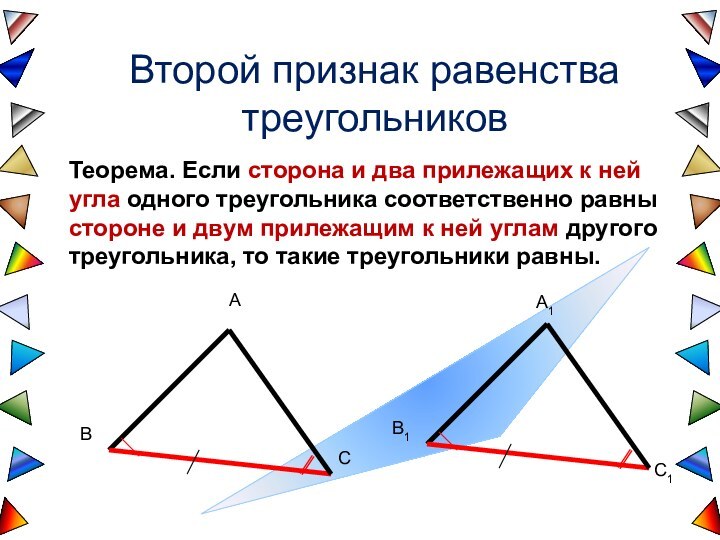
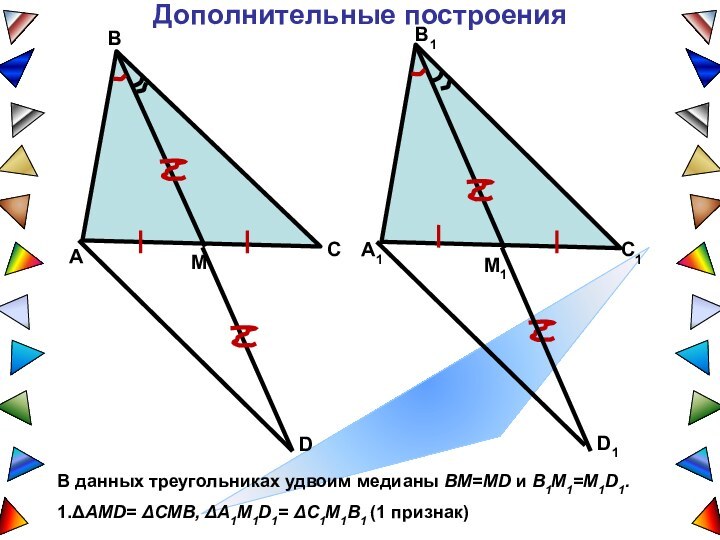
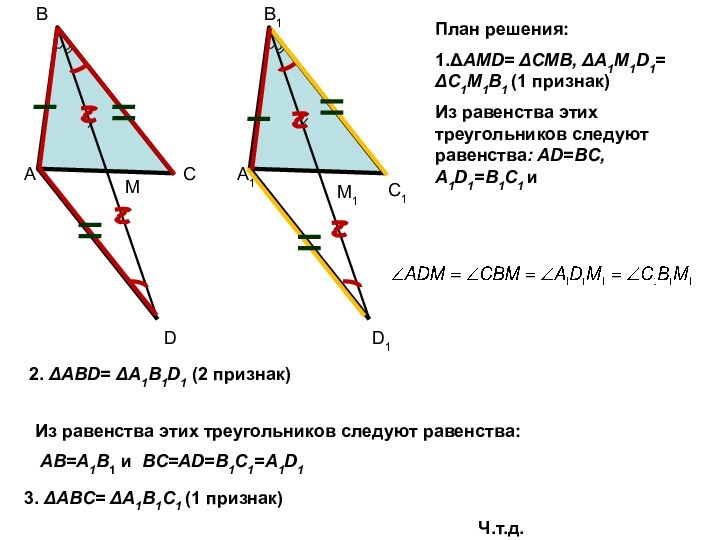
2. ΔABD= ΔA1B1D1 (2 признак)

Из равенства этих треугольников следуют равенства:
AB=A1B1 и BC=AD=B1C1=A1D1

на которые медиана разбивает угол треугольника.

и A 1 B 1 C 1 равны, если

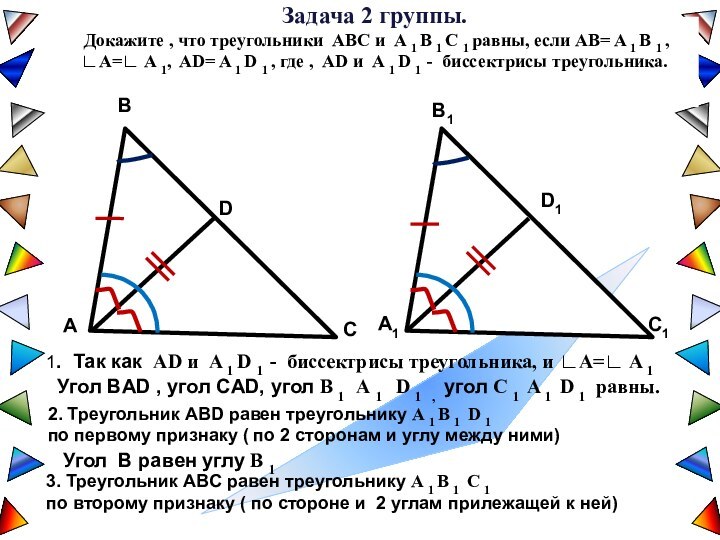
1. Так как AD и A 1 D 1 - биссектрисы треугольника, и ∟А=∟ A 1

Угол BAD , угол CAD, угол В 1 А 1 D 1 , угол С 1 A 1 D 1 равны.

2. Треугольник ABD равен треугольнику A 1 B 1 D 1
по первому признаку ( по 2 сторонам и углу между ними)

Угол В равен углу B 1

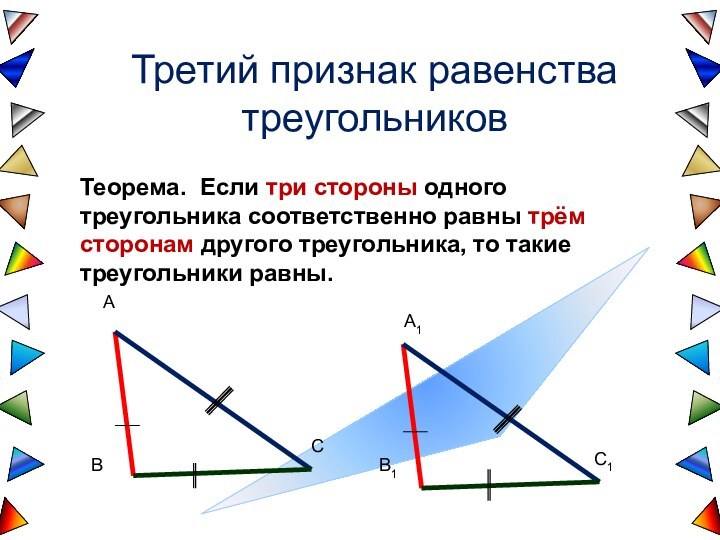
3. Треугольник ABС равен треугольнику A 1 B 1 С 1
по второму признаку ( по стороне и 2 углам прилежащей к ней)

биссектрисе и стороне.