- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение простейших тригонометрических неравенств
Содержание
- 2. Решение неравенств, содержащих тригонометрические функции обычно сводится
- 4. Неравенства : sin x > a, sin
- 6. Тригонометрическое неравенство sin(t)≥a.
- 7. Пример 1 Решите неравенство Нарисуем тригонометрическую окружность и
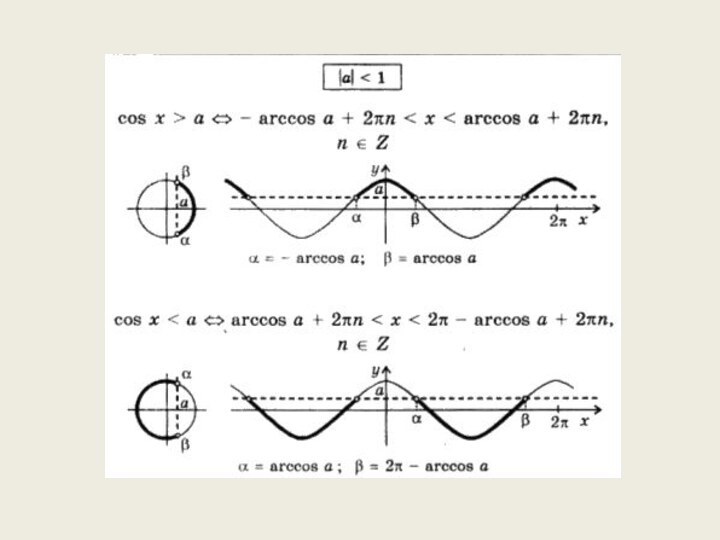
- 10. Тригонометрическое неравенство cos(t)
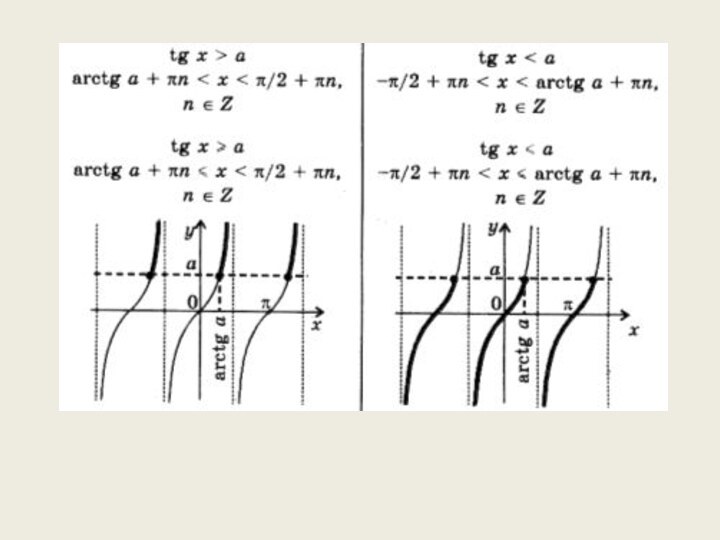
- 12. Тригонометрическое неравенство tg(t)≤a Рассмотрим способ решения
- 13. Скачать презентацию
- 14. Похожие презентации
Решение неравенств, содержащих тригонометрические функции обычно сводится к решению простейших неравенств вида: sin(t);≥)a; cos(t);≥)a; tg(t);≥)a; ctg(t);≥)a; Способы решения этих неравенств совершенно очевидным образом вытекают из представления











Слайд 6
Тригонометрическое неравенство sin(t)≥a.
Все
точки Pt единичной окружности при значениях t, удовлетворяющих данному
неравенству, имеют ординату, большую или равную -1/2. Множество таких точек это дуга l, которая выделена жирным на рисунке ниже. Найдем условие принадлежности точки Pt этой дуге. Точка Pt лежит на правой полуокружности, ордината Pt равна 1/2, и, следовательно, в качестве t1 удобно взять значение t1=arcsin(-1/2)=-π/6. Представим себе, что мы совершаем обход дуги l от точки Pt1 к Pt2 против часовой стрелки. Тогда t2 > t1, и, как легко понять, t2=π-arcsin(-1/2)=7*π/6. Таким образом, получаем, что точка Pt принадлежит дуге l, если -π/6 ≤ t ≤ 7*π/6. Таким образом, решения неравенства, принадлежащие промежутку [-π/2 ; 3*π/2] длиной 2*π таковы: -π/6 ≤ t ≤ 7*π/6. Вследствие периодичности синуса остальные решения получаются добавлением к найденным чисел вида 2πn, где n - целое. Таким образом, мы приходим к ответу: -π/6+2πn≤t≤7π/6+2πn, n - целое.
Слайд 7
Пример 1
Решите неравенство
Нарисуем тригонометрическую окружность и отметим
на ней точки, для которых ордината превосходит
Для x
[0; 2π] решением данного неравенства будут Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2π n то sin x также будет не меньше Следовательно, к концам найденного отрезка решения нужно просто добавить 2π n , где Окончательно, получаем, что решениями исходного неравенства будут все где
Ответ. где