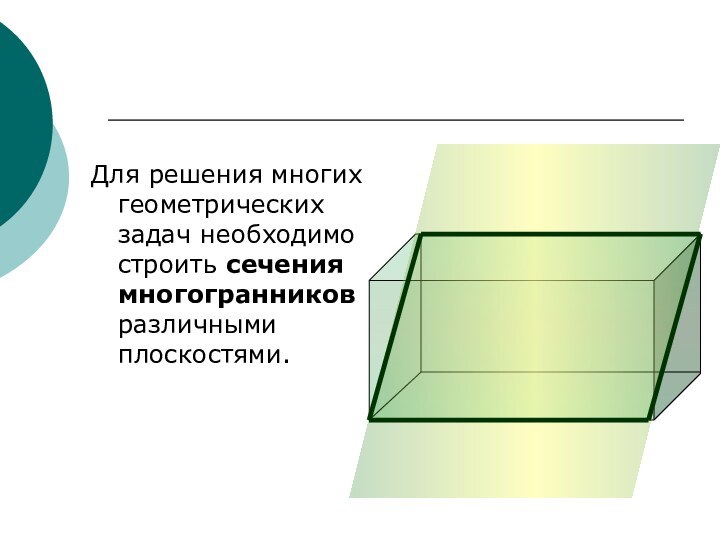
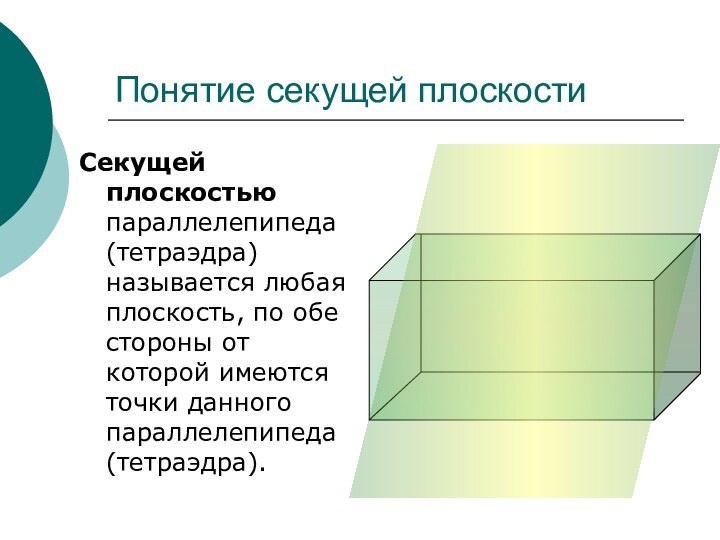
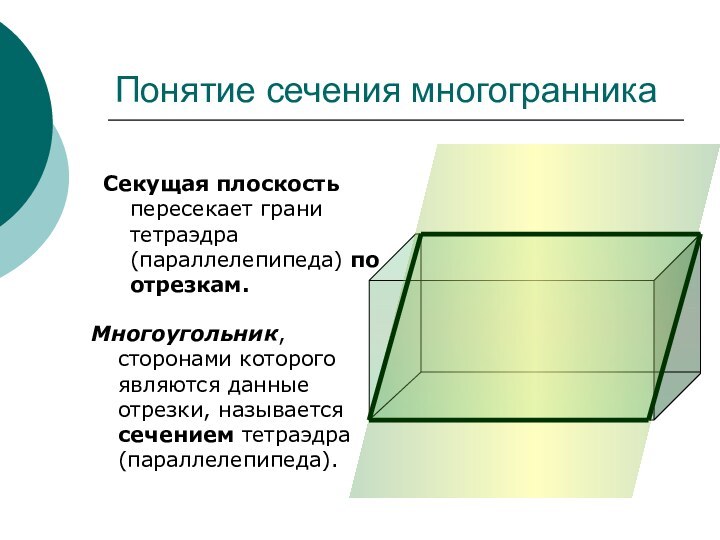
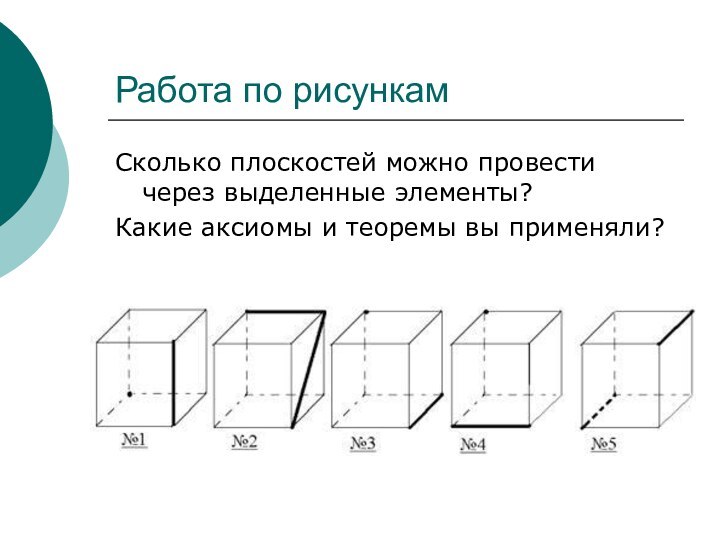
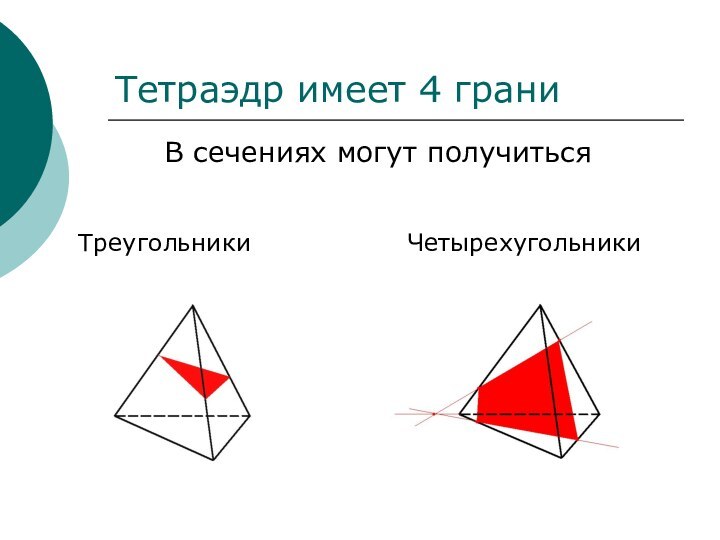
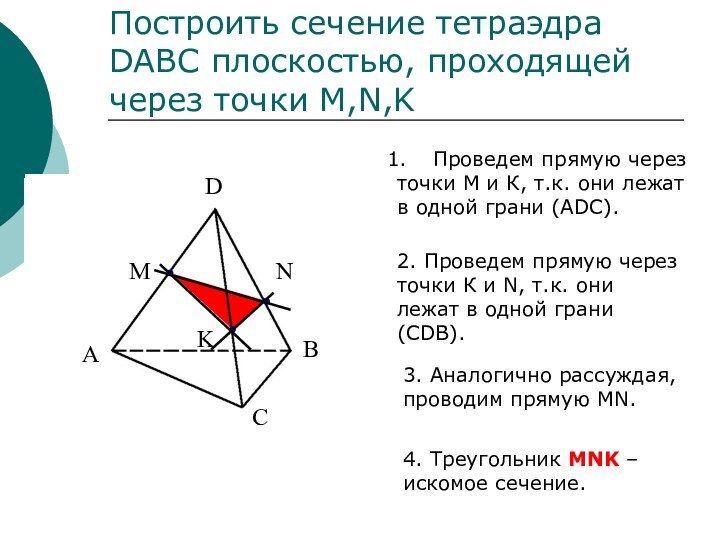
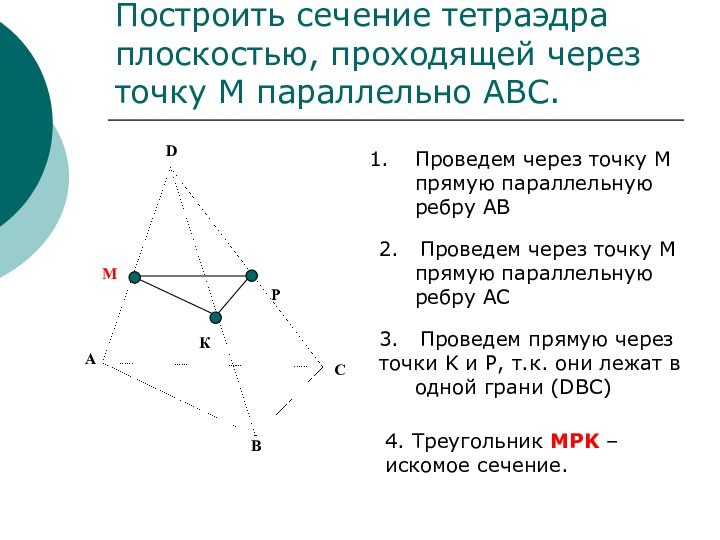
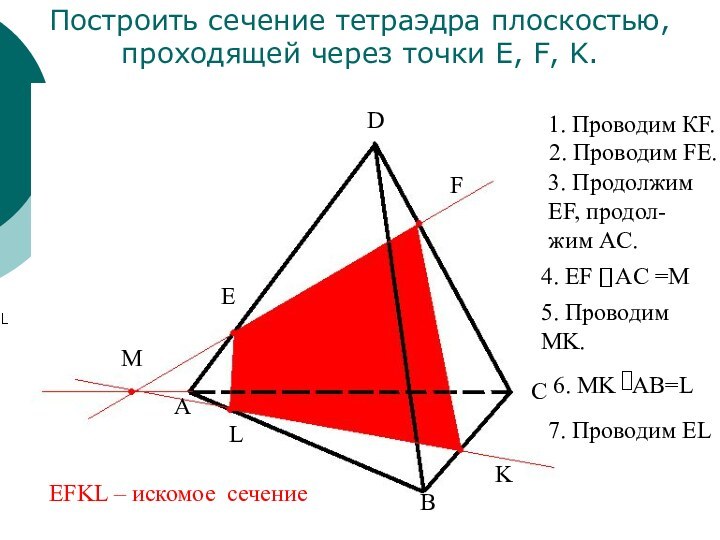
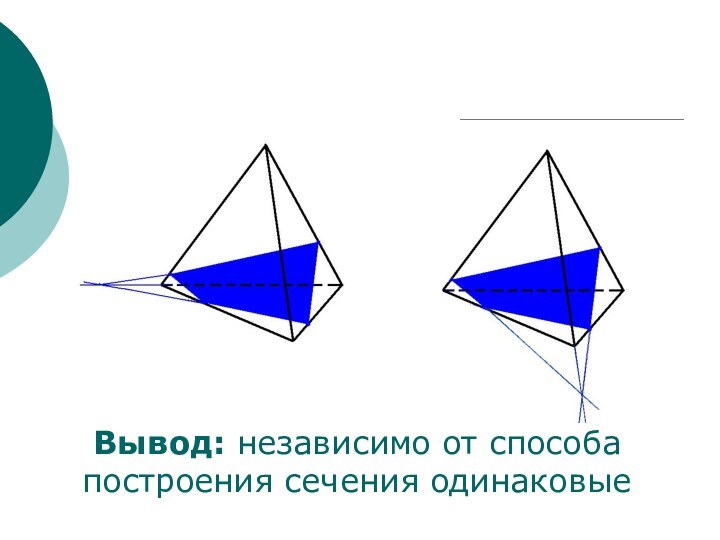
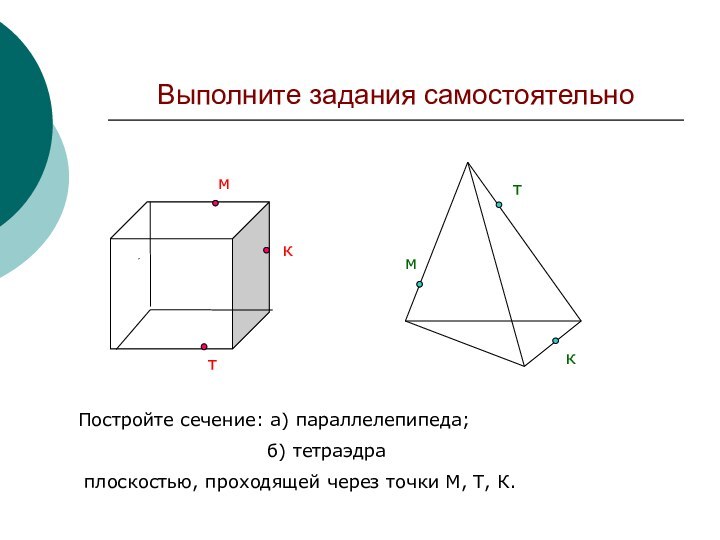
сечений.
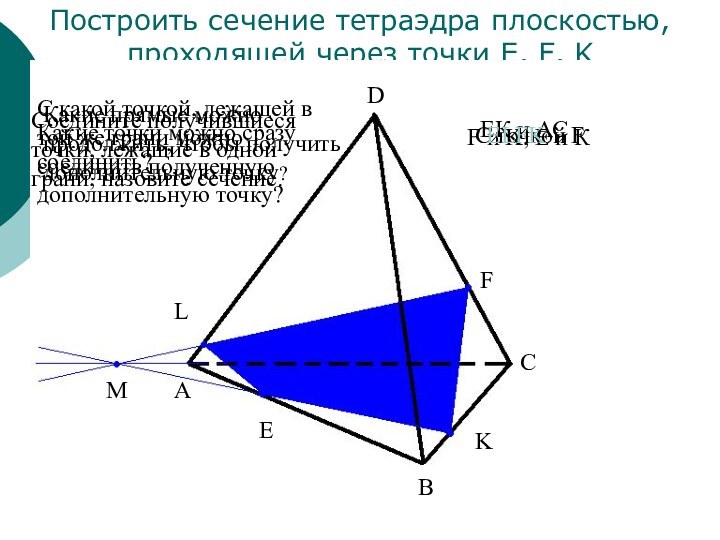
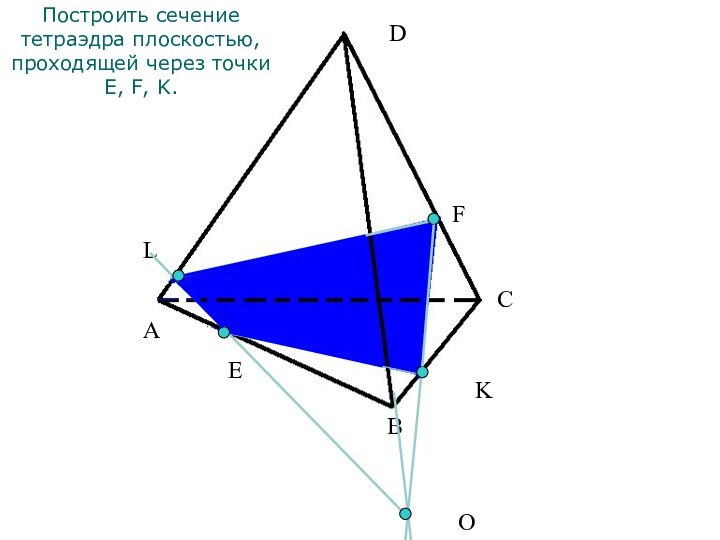
Выработать навыки построения сечений тетраэдра и параллелепипеда при различных
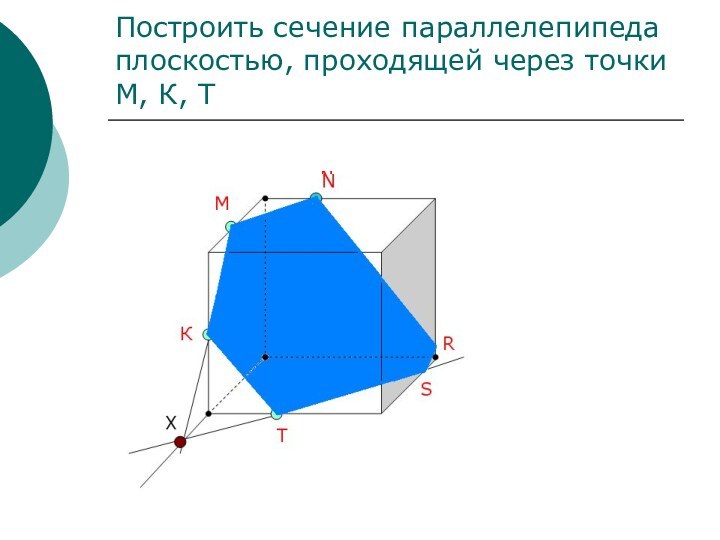
случаях задания секущей плоскости.Сформировать умение применять правила построения сечений при решении задач по темам «Многогранники».