- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрия Лобачевского
Содержание
- 2. Сотни профессиональных геометров разных времён
- 3. Ближе всех к победе над
- 4. Цель:Ознакомление с
- 5. Николай Иванович Лобачевский (1792 – 1856 гг.)Все!
- 6. Отправной пункт геометрии ЛобачевскогоОтправным пунктом геометрии Лобачевского
- 7. Аксиома параллельности ЛобачевскогоВ плоскости Лобачевского через точку C вне
- 8. Три модели геометрии ЛобачевскогоОдной из моих задач
- 9. Модель ПуанкареМодель Пуанкаре (часто называется диск Пуанкаре) —
- 10. Модель КлейнаВ модели Клейна за плоскость принимается
- 11. Интерпретация БельтрамиПервой найденной реальной моделью для планиметрии
- 12. «Чем отличается геометрия Лобачевского от геометрии Евклида?»
- 13. Лобачевский всю жизнь занимался созданной
- 14. Геометрия Лобачевского в нашем миреГеометрия Лобачевского находит
- 15. Данную часть трубы можно считать частью псевдосферы.
- 16. Выводы Ознакомившись с содержанием геометрии Лобачевского, рассмотрев три
- 17. Скачать презентацию
- 18. Похожие презентации
Сотни профессиональных геометров разных времён и народов, тысячи любителей математики в течение 20-х веков искали доказательство пятого постулата. Дальше всех в этих математических битвах зашли учёные XVIII века Саккери (Италия), Ламберт (Швейцария) и Лежандр



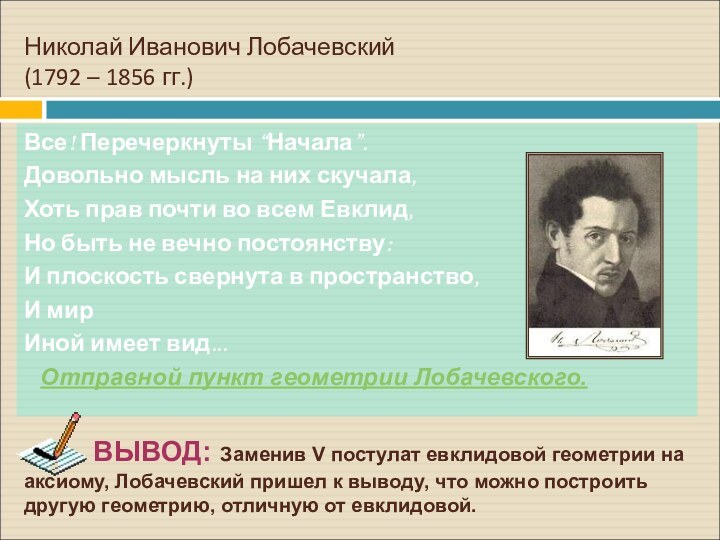








Слайд 3 Ближе всех к победе над пятым
постулатом приблизился великий русский математик Николай Иванович Лобачевский (1792-1856)
Слайд 4
Цель:
Ознакомление с основным
содержанием геометрии Лобачевского
Задачи:
изучить аксиому параллельности геометрии Лобачевского;
изучить три модели
геометрии Лобачевского;сделать сравнительный анализ двух геометрий;
сделать выводы.
Слайд 5
Николай Иванович Лобачевский
(1792 – 1856 гг.)
Все! Перечеркнуты “Начала”.
Довольно мысль на них скучала,
Хоть прав почти во
всем Евклид, Но быть не вечно постоянству:
И плоскость свернута в пространство,
И мир
Иной имеет вид...
Отправной пункт геометрии Лобачевского.
ВЫВОД: Заменив V постулат евклидовой геометрии на аксиому, Лобачевский пришел к выводу, что можно построить другую геометрию, отличную от евклидовой.
Слайд 6
Отправной пункт геометрии Лобачевского
Отправным пунктом геометрии Лобачевского послужил V
постулат Евклида — аксиома, о параллельных прямых. Оказалось то, что
пятый постулат не зависит от предыдущих, а значит, его можно заменить на ему эквивалентный.Аксиоматика планиметрии Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского.
Слайд 7
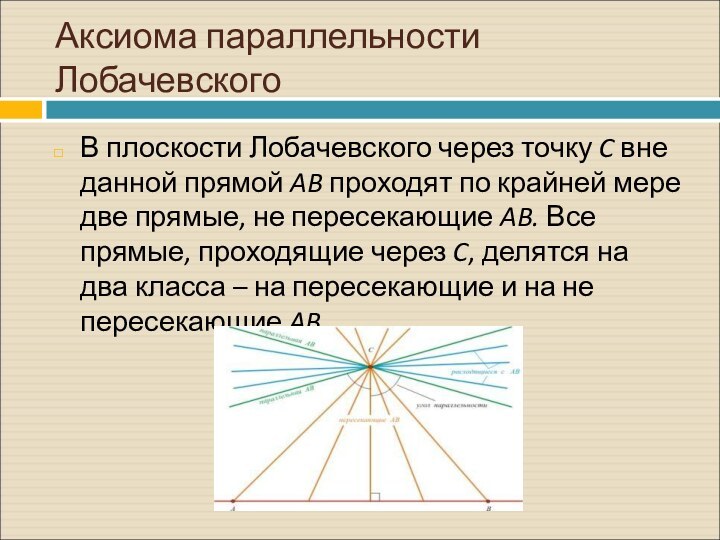
Аксиома параллельности Лобачевского
В плоскости Лобачевского через точку C вне данной
прямой AB проходят по крайней мере две прямые, не пересекающие AB. Все
прямые, проходящие через C, делятся на два класса – на пересекающие и на не пересекающие AB.
Слайд 8
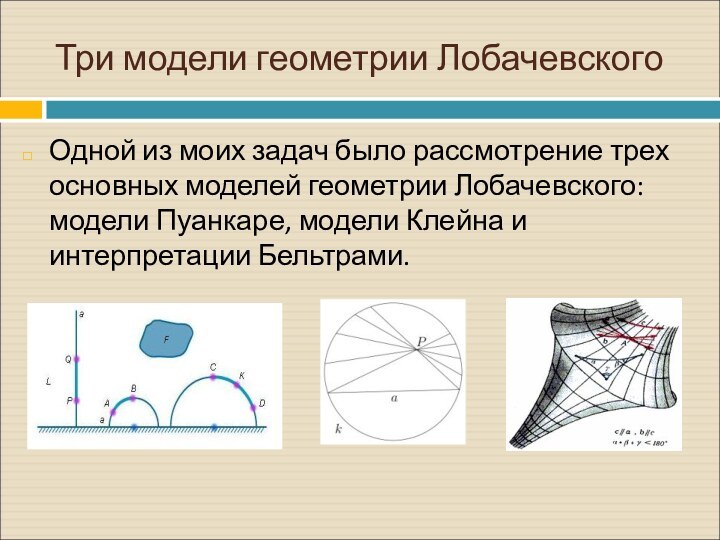
Три модели геометрии Лобачевского
Одной из моих задач было
рассмотрение трех основных моделей геометрии Лобачевского: модели Пуанкаре, модели
Клейна и интерпретации Бельтрами.
Слайд 9
Модель Пуанкаре
Модель Пуанкаре (часто называется диск Пуанкаре) — модель
пространства Лобачевского, предложенная Анри Пуанкаре в 1882 году в связи с задачами теории
функций комплексного переменного. Существуют разновидности модели — в круге и на полуплоскости для планиметрии Лобачевского, а также в шаре и в полупространстве — для стереометрии Лобачевского, соответственно.
Слайд 10
Модель Клейна
В модели Клейна за плоскость принимается внутренность
какой-либо окружности, за точки - точки принадлежащие этому кругу,
за прямые - хорды - конечно, с исключением концов, поскольку рассматривается только внутренность круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями.
Слайд 11
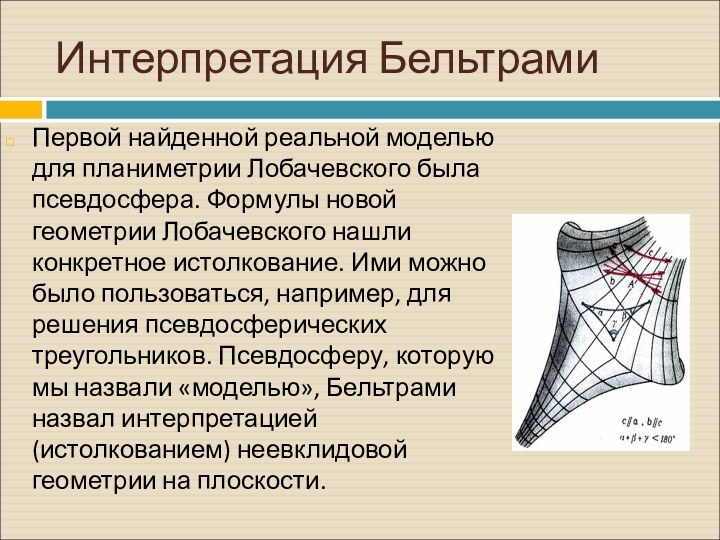
Интерпретация Бельтрами
Первой найденной реальной моделью для планиметрии Лобачевского
была псевдосфера. Формулы новой геометрии Лобачевского нашли конкретное истолкование.
Ими можно было пользоваться, например, для решения псевдосферических треугольников. Псевдосферу, которую мы назвали «моделью», Бельтрами назвал интерпретацией (истолкованием) неевклидовой геометрии на плоскости.
Слайд 12
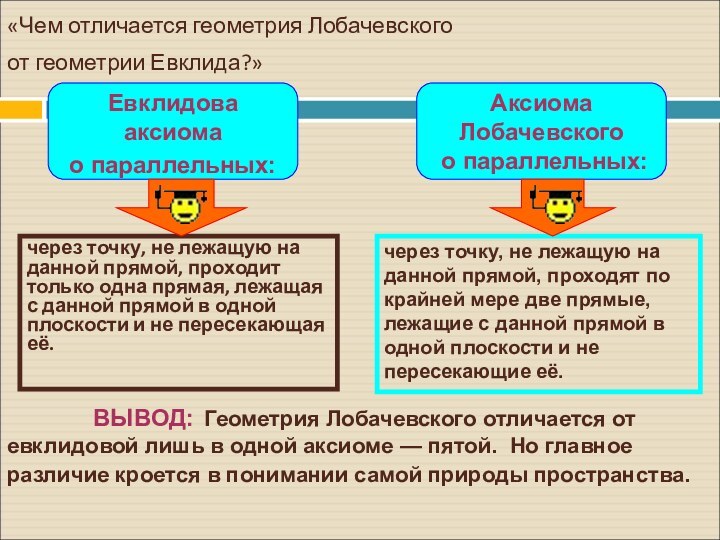
«Чем отличается геометрия Лобачевского
от геометрии Евклида?»
через точку,
не лежащую на данной прямой, проходит только одна прямая,
лежащая с данной прямой в одной плоскости и не пересекающая её.через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
ВЫВОД: Геометрия Лобачевского отличается от евклидовой лишь в одной аксиоме — пятой. Но главное различие кроется в понимании самой природы пространства.
Евклидова аксиома
о параллельных:
Аксиома
Лобачевского
о параллельных: