- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Окружность и круг (9 класс)
Содержание
- 2. КолесоКолесо́ — движитель, круглый (как правило), свободно вращающийся или
- 3. История Самым ранним "колесом" считается находка в
- 4. Геометрия колесаГеометрия колеса основана на геометрии окружности. Параметры
- 5. Изобретая колесоТреугольник Рело — плоская фигура постоянной
- 6. Добавим еще пару параллельных прямых, касающихся треугольника
- 7. Если быть более точным, то надо рассматривать
- 8. Продолжим какую–нибудь сторону правильного треугольника за обе
- 9. Получившаяся красная кривая будет состоять из трех
- 10. Значит, таким образом можно устроить подвеску некруглого колеса с краем в виде красной кривой
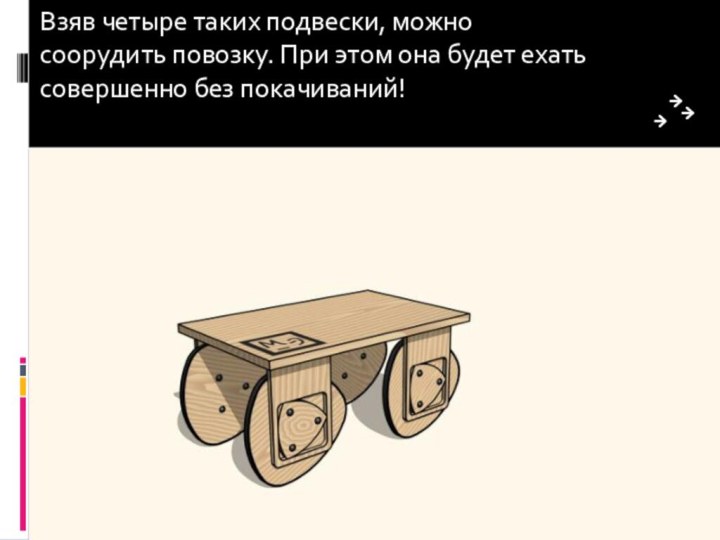
- 11. Взяв четыре таких подвески, можно соорудить повозку. При этом она будет ехать совершенно без покачиваний!
- 12. Дабы убедиться, что тряски нет, поставим, как
- 13. Скачать презентацию
- 14. Похожие презентации
КолесоКолесо́ — движитель, круглый (как правило), свободно вращающийся или закреплённый на оси диск, позволяющий поставленному на него телу катиться, а не скользить. Широко применяется для транспортировки грузов, повсеместно используется в различных механизмах и инструментах.










Слайд 3
История
Самым ранним "колесом" считается находка в Румынии
- ее относят к последней четверти V тысячелетия до
н. э. На одном из поселений в Кукутени румынский археолог М. Дину нашел глиняные модельки колес от игрушечных повозок. Об этом он сообщил в 1981 году. То есть самое первое колесо в истории человечества "появилось" в эпоху неолита на Балканах.Следующие по времени модели колёс были обнаружены археологами А. Д. Резепкиным на Северном Кавказе и А. В. Кондрашовым на Кубани (середина IV тысячелетия).
Таким образом, всё больше материальных доказательств говорят в пользу того, что «самое первое» колесо появилось не на Ближнем Востоке, как это было принято считать до сих пор[3][4][5].
Следующие упоминания о колесе встречаются в Древней Месопотамии в конце 4-го тысячелетия до н. э. Предшественником колеса можно считать известный до этого деревянный каток, который подкладывался под перемещаемый груз. Первоначально колесо представляло собой деревянный диск, насаженный на ось и зафиксированный клином. Изображения салазок с колёсиками (3000 г. до н. э.) найдены в Месопотамии в шумерском городе Урук. К 2700 году до н. э. там же появляются рисунки повозок. В это же время шумеры начинают хоронить своих царей вместе с колесницами. Эти погребения найдены в Кише, Уре, в эламскомгороде Сузы.
Слайд 4
Геометрия колеса
Геометрия колеса основана на геометрии окружности. Параметры окружности
следующие:
Диаметр. Колёса обычно определяются своим диаметром, так как это
определяет их максимальный габарит и, следовательно, является весьма серьёзным ограничивающим фактором в связи с вопросом занимаемого объёма в том или ином механизме.Периметр. Это расстояние, которое проходит колесо по плоскости за один оборот. Таким образом, расстояние, пройденное за заданное число оборотов, определяется периметром, который в свою очередь зависит от диаметра согласно следующему выражению:
Более общее выражение:
Где:
— пройденное расстояние
— угол оборота
r — радиус колеса (D=2r)
Слайд 5
Изобретая колесо
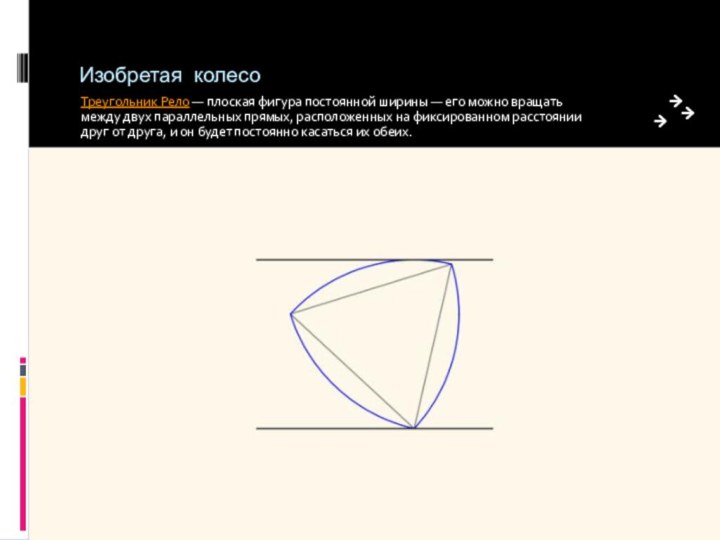
Треугольник Рело — плоская фигура постоянной ширины
— его можно вращать между двух параллельных прямых, расположенных
на фиксированном расстоянии друг от друга, и он будет постоянно касаться их обеих.Слайд 6 Добавим еще пару параллельных прямых, касающихся треугольника Рело
и образующих с уже имеющимися прямой угол. Тем самым
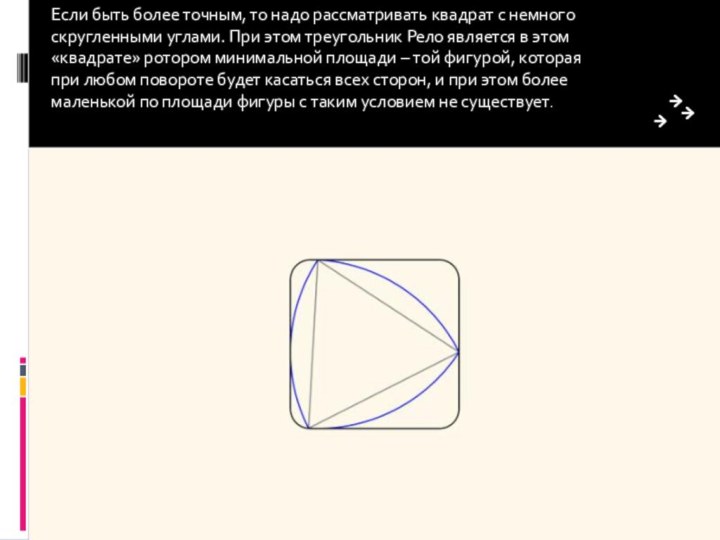
получим квадрат. Если вращать треугольник Рело специальным образом, то он будет постоянно находиться внутри квадрата и в любой момент касаться всех его сторон.Слайд 7 Если быть более точным, то надо рассматривать квадрат
с немного скругленными углами. При этом треугольник Рело является
в этом «квадрате» ротором минимальной площади – той фигурой, которая при любом повороте будет касаться всех сторон, и при этом более маленькой по площади фигуры с таким условием не существует.Слайд 8 Продолжим какую–нибудь сторону правильного треугольника за обе вершины
на одинаковое расстояние. Провращаем получившийся отрезок вокруг одной из
вершин и проследим за траекториями его концов. Полученные большая и малая дуги будут частью кривой, ограничивающей фигуру постоянной ширины, которая строится. Провращаем этот же отрезок вокруг другой вершины, а затем вокруг оставшейся третьей вершины.Слайд 9 Получившаяся красная кривая будет состоять из трех дуг
большого радиуса и трех — малого. Можно доказать, что
она является границей фигуры постоянной ширины. При этом неважно, насколько продолжать сторону за вершины, главное, чтобы за обе вершины сторона продолжалась на одинаковое расстояние.Если начать вращать треугольник Рело в квадрате, то связанная с ним красная кривая будет вращаться между двух параллельных прямых, неподвижных относительно квадрата.