- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по Геометрии Теорема об углах, образованных двумя параллельными прямыми и секущей
Содержание
- 2. Как называются углы при прямых m и l и секущей h?
- 3. Если при пересечении двух
- 4. Аксиома параллельных прямых
- 5. Через точку, не лежащую
- 6. Теоремы об углах, образованных двумя параллельными прямыми и секущей
- 7. Если две параллельные прямые пересечены
- 8. bаc3Дано: а II b, c- секущая. Доказать:
- 9. 12bаc3Дано: а II b, c- секущая. Доказать:
- 10. ab 2 1ab 136 1 440 440aIIbaIIb
- 11. Домашнее задание:стр. 58 – 63, учить аксиомы,
- 12. Используя данные рисунка, найдите углы 1, 2 и 3.аbсd 2001200 1600123
- 13. Может ли еще один из семи остальных
- 14. 2х+300х1х 2= х+30
- 15. Тренировочные упражнения21bаcУгол 1 в 4 раза больше угла 2х4х
- 16. Тренировочные упражнения21bаcДано: а II b, с –
- 17. Тренировочные упражнения21bаcДано: а II b, с –
- 18. Тренировочные упражнения21bаcДано: а II b, с –
- 19. Тренировочные упражнения21bаcДано: а II b, с –
- 20. 21bаcДано: а II b, с – секущая
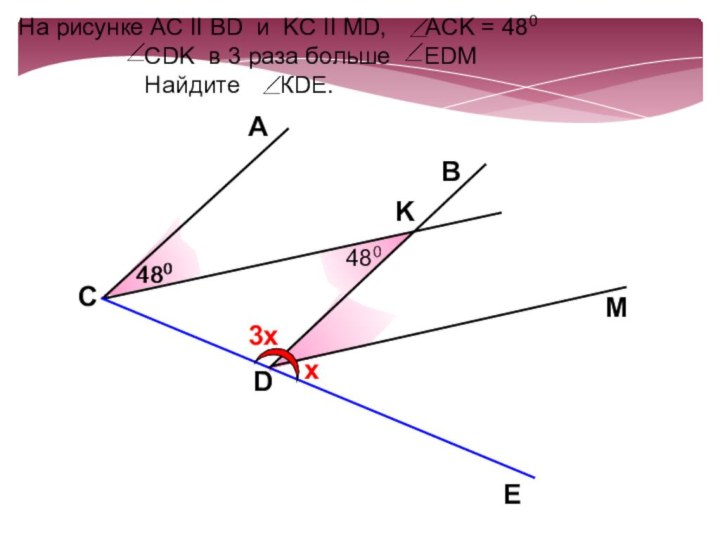
- 21. На рисунке АС II ВD и
- 22. EDAПостроим CN II ABBCПодсказка
- 23. EDAПостроим CN II ABBCПодсказка14001300400500На рисунке АВ II
- 24. На рисунке a II b, c –
- 25. ADE 340BCMK1460 340?N
- 26. Скачать презентацию
- 27. Похожие презентации
























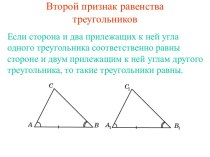
Слайд 3 Если при пересечении двух прямых
секущей соответственные углы равны,
то прямые параллельны. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
1
2
а
b
c
c
а
b
1
2
c
а
b
1
2
Если при пересечении двух прямых
секущей накрест лежащие углы равны,
то прямые параллельны.
Признаки параллельности прямых
Слайд 5 Через точку, не лежащую на
данной
прямой, проходит только одна прямая, параллельная
данной. Следствие 1.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
a II b, c ∩ b ⇒ c ∩ a
а
А
Следствие 2.
Если две прямые параллельны третьей прямой, то они параллельны.
a II с, b II с ⇒ a II b
c
b
Слайд 7 Если две параллельные прямые пересечены секущей,
то накрест лежащие углы равны.
а
b
M
N
Дано: a II b, MN-
секущая.Доказать: 1= 2 (НЛУ)
Доказательство:
способ от противного.
Допустим, что 1 2.
1
2
Р
Слайд 8
b
а
c
3
Дано: а II b, c- секущая.
Доказать: OУ
1+ 2=1800.
Доказательство:
3+
2 =1800, т. к. они смежные.1= 3, т. к. это НЛУ при а II b
3 + 2 =1800
1
Теорема доказана.
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800.
Слайд 9
1
2
b
а
c
3
Дано: а II b, c- секущая.
Доказать: СУ
1 = 2.
Доказательство:
2
= 3, т. к. они вертикальные.3 = 1, т. к. это НЛУ при а II b
1 = 3 = 2
Теорема доказана.
Если две параллельные прямые пересечены секущей, соответственные углы равны.
Слайд 11
Домашнее задание:
стр. 58 – 63, учить аксиомы, теоремы
и их доказательства; решить задачи № 205, 207, 209.
Слайд 13 Может ли еще один из семи остальных углов,
образованных при пересечении прямых a и b с прямой
d, быть равен 1100? 600? Почему?а
b
m
d
1100
400
400
400
1100
1100
1100
Слайд 14
2
х+300
х
1
х
2= х+30
1800,
т.к. ОУ при а II bВОА=х,
Составь уравнение…
Найди сам угол.
М
N
В
A
B
Задача
Если MN II AB, а угол 2 больше угла 1 на 300, то угол 2 равен…
Решение:
1= х,
2= х+30
1= ВОС,
они вертикальные.
С
Слайд 16
Тренировочные упражнения
2
1
b
а
c
Дано: а II b, с – секущая
1 –
2 = 300Найдите: 1 и 2
х
х+30
Угол 1 на 300 больше угла 2
Слайд 17
Тренировочные упражнения
2
1
b
а
c
Дано: а II b, с – секущая
2 =
0,8 1Найдите: 1 и 2
Угол 2 составляет 0,8 части угла 1
х
0,8х
Слайд 18
Тренировочные упражнения
2
1
b
а
c
Дано: а II b, с – секущая
1 :
2 = 5 : 4Найдите: 1 и 2
5х
4х
Пусть х – 1 часть
Слайд 19
Тренировочные упражнения
2
1
b
а
c
Дано: а II b, с – секущая
2 составляет 80% от 1
Найдите:
1 и 2х
0,8х
Слайд 20
2
1
b
а
c
Дано: а II b, с – секущая
1 :
2 = 5 : 4Найдите: 1 и 2
5х
4х
AB = BC, A=600,
CD – биссектриса угла ВСЕ.
Докажите, что АВ II CD.
A
С
B
D
E
600
600
1200
600
600
биссектриса
Пусть х – 1 часть
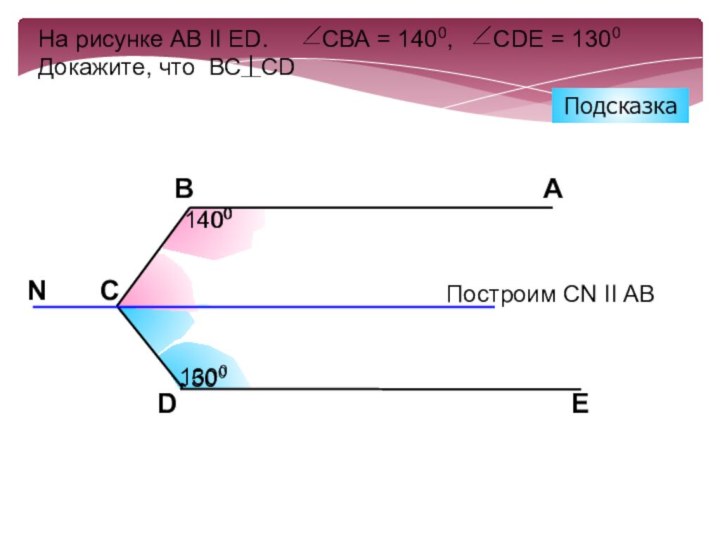
Слайд 23
E
D
A
Построим CN II AB
B
C
Подсказка
1400
1300
400
500
На рисунке АВ II ЕD.
CВА = 1400, СDE
= 1300Докажите, что ВС СD
Слайд 24 На рисунке a II b, c – секущая,
DM и DN – биссектрисы смежных углов, образованных прямыми
a и c. DE = 5,8 смНайдите MN.
с
D
M
400
E
а
b
N
5,8 см
?