- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Этот самый знаменитый
Содержание
- 2. (Отрывок из стихотворения А. Шамиссо)теорема Пифагора
- 3. Пифагор
- 4. О жизни
- 6. Теорема Пифагора "Пифагоровы штаны Во все стороны равны"
- 7. Доказательство теоремы считалось в кругах учащихся средних
- 8. В некоторых списках «Начал» Евклида теорема Пифагора
- 9. «В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 10. Доказательство:Достроим данный треугольник до квадрата со стороной
- 11. История теоремы В истории древнего
- 12. Кантор (крупнейший немецкий математик) считает, что равенство
- 13. В самом древнем индийском геометрическом сборнике «Сульвасутра»
- 14. Как свидетельствуют летописи, в Древнем Китае уже
- 15. Не подлежит, однако, сомнению, что эту теорему
- 16. В конце
- 17. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА
- 18. Трудно
- 19. О теореме
- 20. Этот
- 21. Старинные задачи:
- 22. 125² = 117² + Х²X² = 125²
- 23. Часто математики записывали свои задачи в стихотворной
- 24. Решение:3² + 4² = x²X² = 25X
- 25. Еще одна задача древних индусов также предложенная в стихах:
- 26. Решение:(Х + ½)² – X² = 2²X²
- 27. С аэродрома вылетели одновременно два самолёта: один
- 28. По теореме Пифагора: 4x2+(0,75x·2)2=20002 6,25x2=20002 2,5x=2000 x=800 0,75x=0,75·800=600.Ответ: 800 км/ч.; 600 км/ч РЕШЕНИЕ:
- 29. Скачать презентацию
- 30. Похожие презентации
























Слайд 4
О жизни
Пифагора известно немного. Он родился в 580 г. до
н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.
Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки.
Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги – в образе полулюдей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки.
Слайд 5
Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и
применяли при счёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений.Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне.
Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.
Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду.
Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов.
Наука Вавилона была более развитой, нежели египетская.
Слайд 7
Доказательство теоремы считалось в кругах учащихся средних веков
очень трудным и называлось:
“Dons asinorum” -
«ослиный мост»
или
“elefuga”
-«бегство убогих»
«ветряной мельницей»,
«теоремой – бабочкой»
или
«теоремой невесты»
а сама теорема –
Слайд 8 В некоторых списках «Начал» Евклида теорема Пифагора называлась
теоремой Нимфы, «теорема – бабочка», по-видимому из-за сходства чертежа
с бабочкой, поскольку словом «нимфа» греки называли бабочек. Нимфами греки называли еще и невест, а также некоторых богинь.При переводе с греческого арабский переводчик, вероятно, не обратил внимания на чертеж и перевел слово «нимфа» не как «бабочка», а как «невеста». Так и появилось ласковое название знаменитой теоремы – «Теорема Невесты».
Слайд 9
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов
катетовкатетов».
Формулировки теоремы Пифагора различны.Общепринятой считается следующая:
Во времена
Пифагора формулировка теоремы звучала так:
Слайд 10
Доказательство:
Достроим данный треугольник до квадрата со стороной (a
+ b) так, как показано на рисунке.
Sкв. = (a
+ b)² или Sкв. = 4Sтр. + S`кв.Sтр. = ab; Sкв. = c², тогда
Sкв. = 4· ab + c²
Таким образом, (a + b)² = 4· ab + c²
a² + 2ab + b² = 2ab + c²
a² + b²= c²
Слайд 11
История теоремы
В истории древнего Китая
особое внимание привлекает
математическая книга Чу-пей.
В этом сочинении так говорится о пифагоровом
треугольнике со сторонами 3, 4 и 5:
"Если прямой угол разложить на составные
части, то линия, соединяющая концы его
сторон, будет 5, когда основание есть 3,
а высота 4".
В этой же книге предложен рисунок, который совпадает с
одним из чертежей индусской геометрии Басхары.
Слайд 12 Кантор (крупнейший немецкий математик) считает, что равенство 3 ² + 4 ² = 5² было известно
уже египтянам еще около 2300 г. до н. э.,
во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.
Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.
Слайд 13 В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила
веревки», 600 год до н.э.), представляющем собой своеобразную инструкцию
по сооружению алтарей в храмах, даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины). Алтари по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта.4
3
5
Слайд 14 Как свидетельствуют летописи, в Древнем Китае уже около
2200 года до н.э. для треугольника со сторонами 3,
4, 5 было найдено правило «гоу-гу», с помощью которого можно было по известным гипотенузе и одному из катетов находить другой неизвестный катет, а также гипотенузу, если известны оба катета.Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике.
Слайд 15 Не подлежит, однако, сомнению, что эту теорему знали
за много лет до Пифагора. Так, за 1500 лет
до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий.Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол.
Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий.
Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол.
Слайд 16 В конце девятнадцатого
века высказывались разнообразные предположения о существовании обитателей Марса подобных
человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы которые долгое время считались исскуственными) .Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора.Неизвестно,как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.Слайд 18 Трудно найти
человека, у которого имя Пифагора не ассоциировалось бы с
его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о "пифагоровых штанах" - квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора это её простота, красота, значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о её широком применении.
Слайд 19
О теореме Пифагора
в своих работах писали многие учёные: греческий писатель-моралист Плутарх,
математик V века Прокл и другие. Возможно, кто-то из вас читал сонет немецкого писателя - романиста Шамиссо: Пребудет вечной истина, как скоро Её узнает слабый человек! И ныне теорема Пифагора Верна, как и в его далёкий век. Обильно было жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, её почуя, вслед. Они не в силах свету помешать, А могут лишь, закрыв глаза, дрожать От страха, что вселил в них Пифагор.Слайд 20 Этот рассказ
о жертвоприношении, сообщаемый Диогеном, Лаэртом и Плутархом, конечно вымышлен.
А поэтому, увы, лишено основания и то насмешливое замечание о переселении душ, которое встречается у Генриха Гейне: "Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принёс в жертву бессмертным богам".
Слайд 22
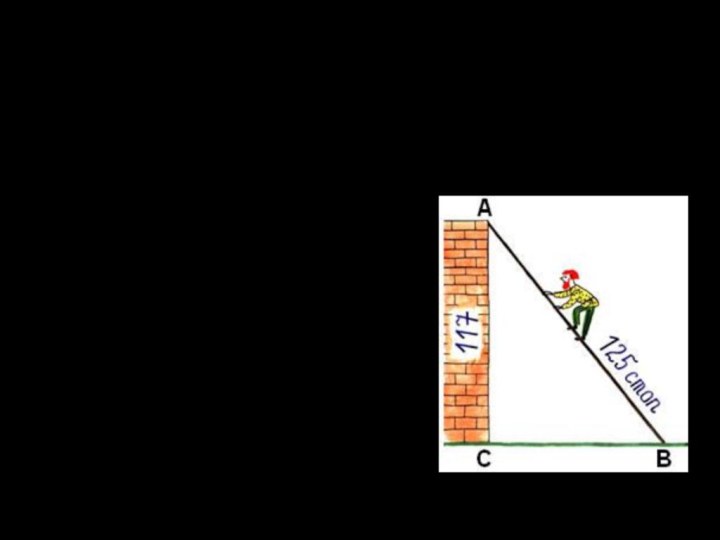
125² = 117² + Х²
X² = 125² –
117²
X² = (125 – 117)·(125 + 117)
X² = 8·242
X²
= 4·4·121X = 2·2·11
X = 44(стопы) – нижний конец лестницы отстоит от стены
Решение:
Эта задача взята из первого учебника математики на Руси. Называется этот учебник «Арифметика», а автор его Леонтий Филиппович Магницкий.
Слайд 23 Часто математики записывали свои задачи в стихотворной форме.
Вот одна из задач индийского математика XII века Бхаскары:
Слайд 24
Решение:
3² + 4² = x²
X² = 25
X =
5(футов) – длина отломленной части ствола;
3 + 5 =
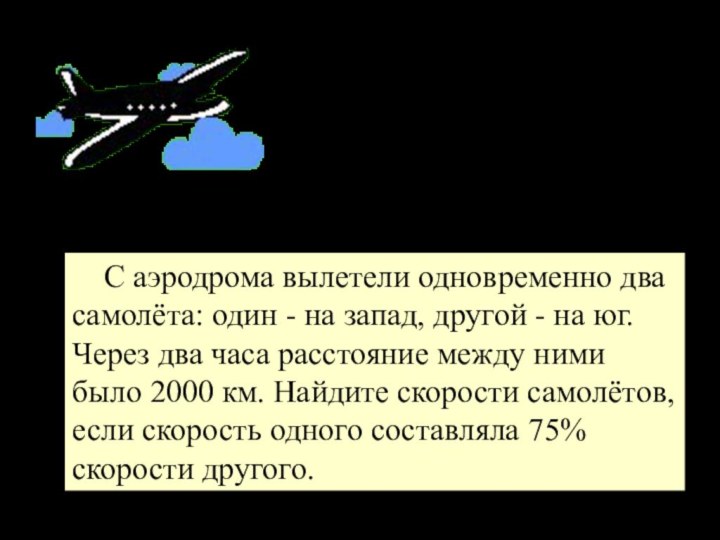
8(футов) – высота тополя.Слайд 27 С аэродрома вылетели одновременно два самолёта: один -
на запад, другой - на юг. Через два часа
расстояние между ними было 2000 км. Найдите скорости самолётов, если скорость одного составляла 75% скорости другого.ЗАДАЧА