- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Материалы к уроку по стереометрии на тему Перпендикуляр и наклонные (10 класс)
Содержание
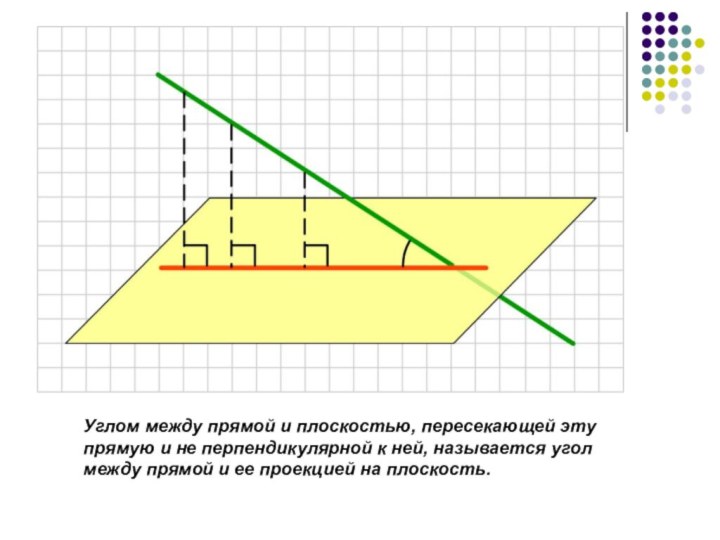
- 2. Расстояние от точки до плоскостиТеорема о трех перпендикулярахПроекция на плоскостьУгол между прямой и плоскостью
- 3. Расстояние от точки до плоскостиАαМHПерпендикуляр, проведенный из
- 4. Перпендикуляр, наклонная и ее проекция образуют прямоугольный
- 5. Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.α║β
- 6. m║αРасстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
- 7. abРасстояние между одной из скрещивающихся прямых и
- 8. Теорема о трех перпендикулярахПрямая, проведенная в плоскости
- 9. αАМНаОбратная теоремаПрямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
- 10. Проекцией точки на плоскость называется основание перпендикуляра,
- 11. ABA1B1Проекцией отрезка АВ, не перпендикулярного к плоскости,
- 12. Если построить проекции всех точек фигуры F
- 13. Проекция детали
- 14. Свойства проекцииПусть из одной точки к плоскости проведены перпендикуляр и несколько наклонных.Тогда справедливы следующие утверждения:
- 15. Любая наклонная длиннее как перпендикуляра, так и проекции наклонной на эту плоскость.
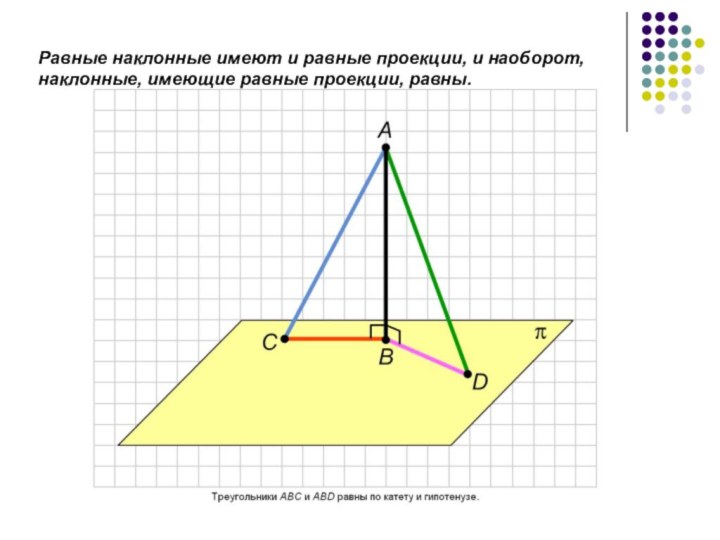
- 16. Равные наклонные имеют и равные проекции, и наоборот, наклонные, имеющие равные проекции, равны.
- 17. Одна наклонная длиннее другой тогда и только тогда, когда проекция первой наклонной длиннее проекции второй наклонной.
- 18. Скачать презентацию
- 19. Похожие презентации
Расстояние от точки до плоскостиТеорема о трех перпендикулярахПроекция на плоскостьУгол между прямой и плоскостью












Слайд 3
Расстояние от точки до плоскости
А
α
М
H
Перпендикуляр, проведенный из данной
точки к плоскости, меньше любой наклонной, проведенной из той
же точки к этой плоскости.АН – перпендикуляр,
точка Н – основание перпендикуляра,
отрезок АМ – наклонная,
точка М – основание наклонной,
отрезок НМ – проекция наклонной на плоскость.
•
•
Слайд 4
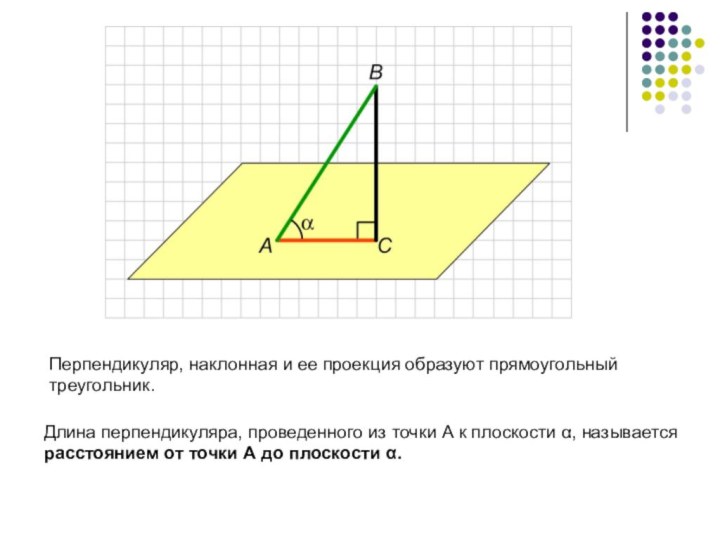
Перпендикуляр, наклонная и ее проекция образуют прямоугольный треугольник.
Длина
перпендикуляра, проведенного из точки А к плоскости α, называется
расстоянием от точки А до плоскости α.Слайд 5 Расстояние от произвольной точки одной из параллельных плоскостей
до другой плоскости называется расстоянием между параллельными плоскостями.
α║β
Слайд 6
m║α
Расстояние от произвольной точки прямой до плоскости называется
расстоянием между прямой и параллельной ей плоскостью.
Слайд 7
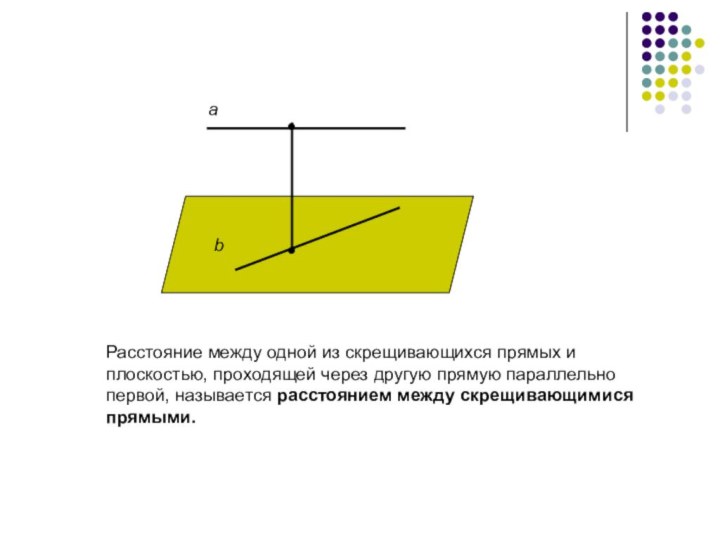
a
b
Расстояние между одной из скрещивающихся прямых и плоскостью,
проходящей через другую прямую параллельно первой, называется расстоянием между
скрещивающимися прямыми.•
•
Слайд 8
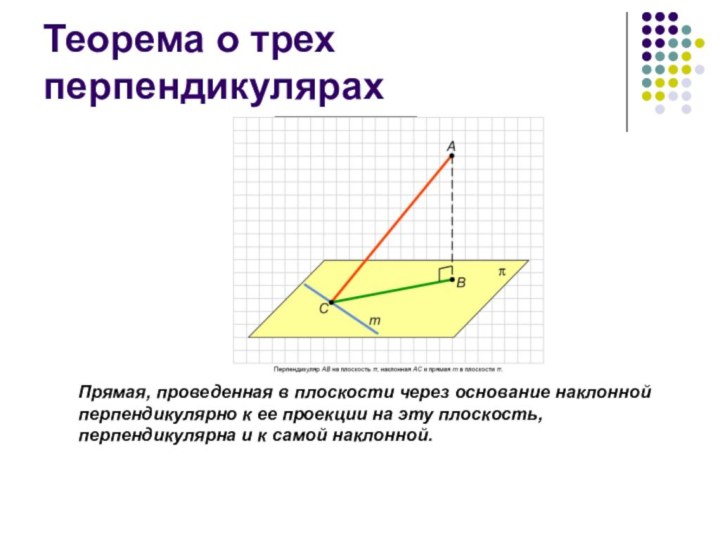
Теорема о трех перпендикулярах
Прямая, проведенная в плоскости через
основание наклонной перпендикулярно к ее проекции на эту плоскость,
перпендикулярна и к самой наклонной.α
А
М
Н
а
Слайд 9
α
А
М
Н
а
Обратная теорема
Прямая, проведенная в плоскости через основание наклонной
перпендикулярно к ней, перпендикулярна и к ее проекции.
Слайд 10 Проекцией точки на плоскость называется основание перпендикуляра, проведенного
из этой точки к плоскости, если точка не лежит
в плоскости, и сама точка, если она лежит в плоскости.
Слайд 11
A
B
A1
B1
Проекцией отрезка АВ, не перпендикулярного к плоскости, является
отрезок, концами которого служат проекции точек А и В.
Слайд 12 Если построить проекции всех точек фигуры F на
данную плоскость, то получим фигуру F1, которая называется проекцией
фигуры F на данную плоскость.F
F1