- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме: Теорема Пифагора
Содержание
- 2. Тема урока:"Теорема Пифогора"
- 3. Устная работа. 2. Историческая справка. 3. Доказательство
- 4. Цель урока: Расмотреть теорему Пифагора и показать ее применение в ходе решения задач.
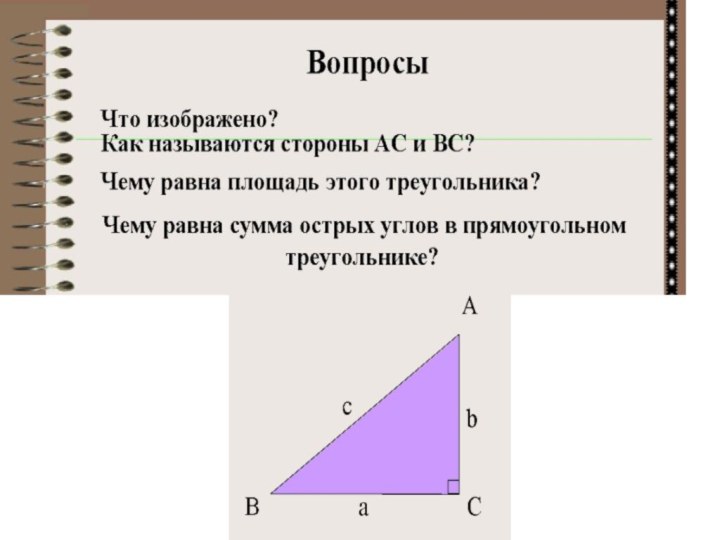
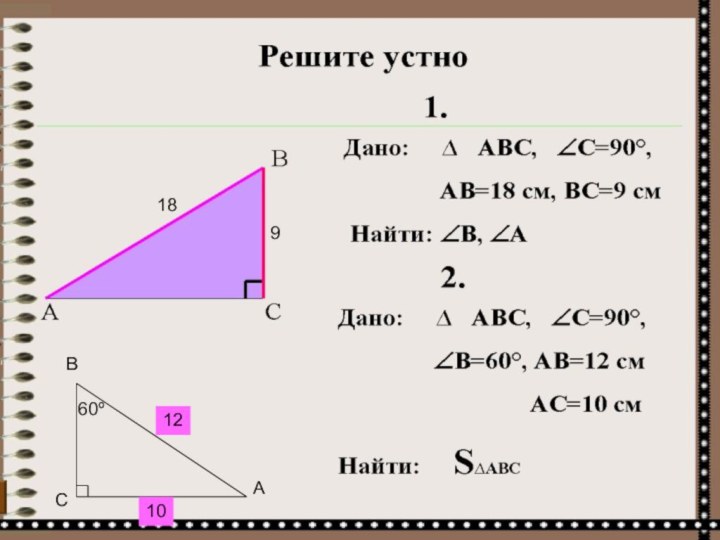
- 5. Устная работа
- 8. 18 9ABC121060º
- 9. Историческая справка
- 10. ПифагорПифагор Самосский(около 570-около 500 до н.э.) древнегреческий
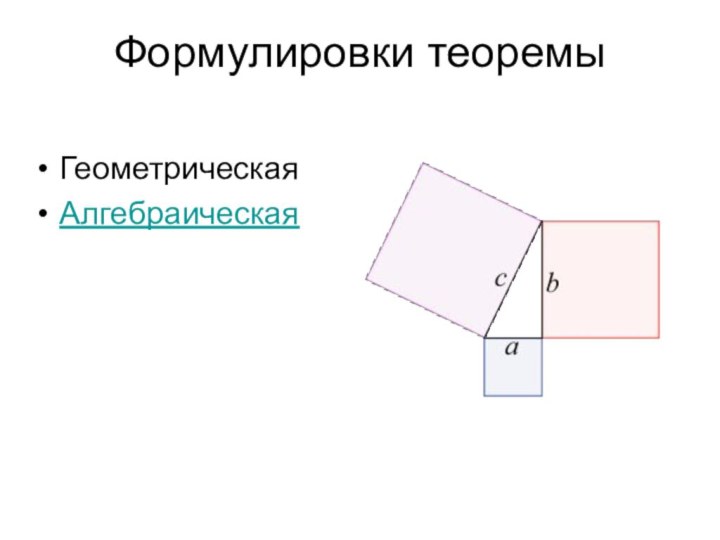
- 11. Формулировки теоремыГеометрическаяАлгебраическая
- 12. ГеометрическаяВ прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
- 13. АлгебраическаяВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. a²+b²=c² АВ²=АС²+ВС²АвСсаb
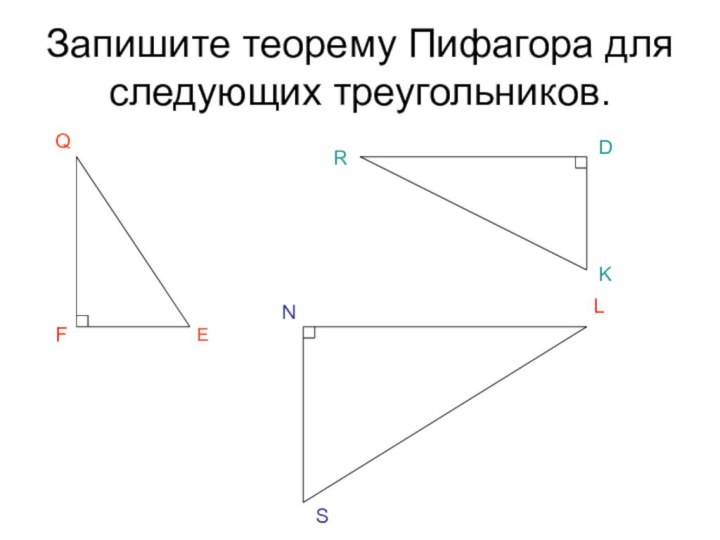
- 14. Запишите теорему Пифагора для следующих треугольников. EFQRDKNLS
- 15. EFQRDKNLSQE²=QF²+EF²RK²=RD²+DK²LS²=NS²+NL²
- 16. Доказательство теоремы Пифагора
- 17. ДоказательстваВ научной литературе зафиксировано 367 доказательств данной
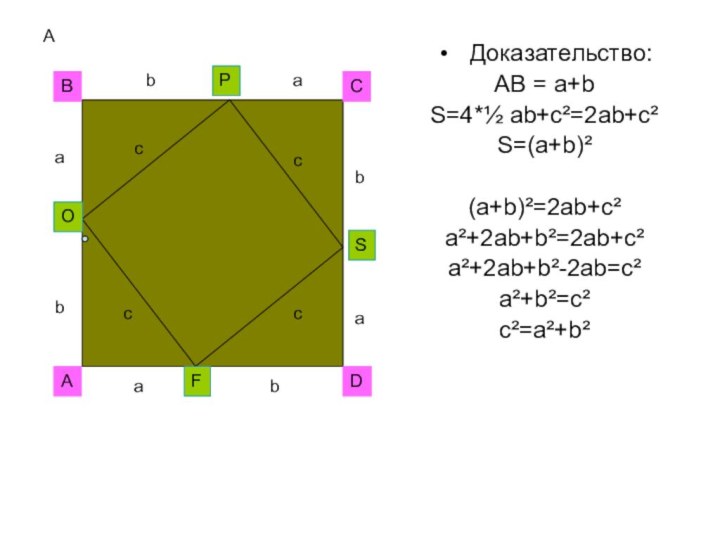
- 18. А Доказательство:AB = a+bS=4*½ ab+c²=2ab+c²S=(a+b)²(a+b)²=2ab+c²a²+2ab+b²=2ab+c²a²+2ab+b²-2ab=c²a²+b²=c²c²=a²+b² АВСDааааbbbbOPSFcccc
- 22. Решение задач по готовым чертежам.
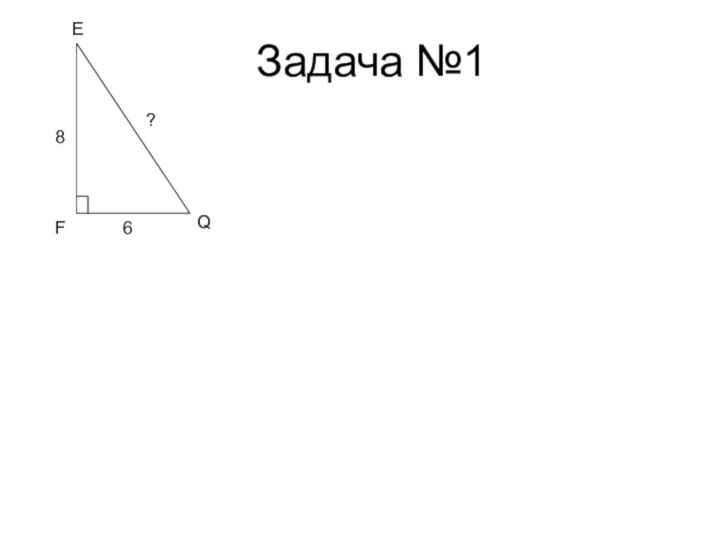
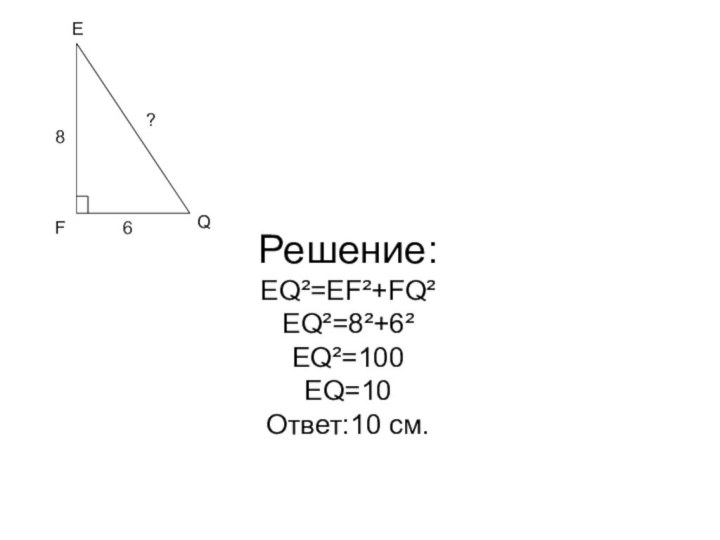
- 23. Задача №1FEQ68?
- 24. Решение: EQ²=EF²+FQ² EQ²=8²+6² EQ²=100 EQ=10 Ответ:10 см. FEQ68?
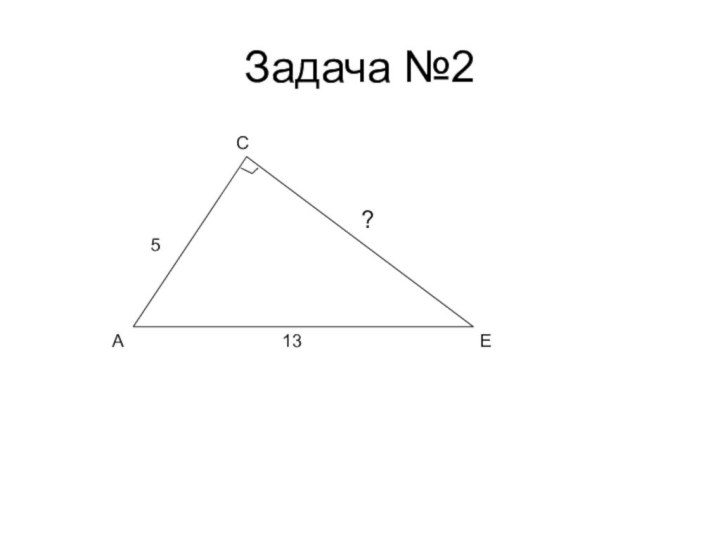
- 25. Задача №2AEC135?
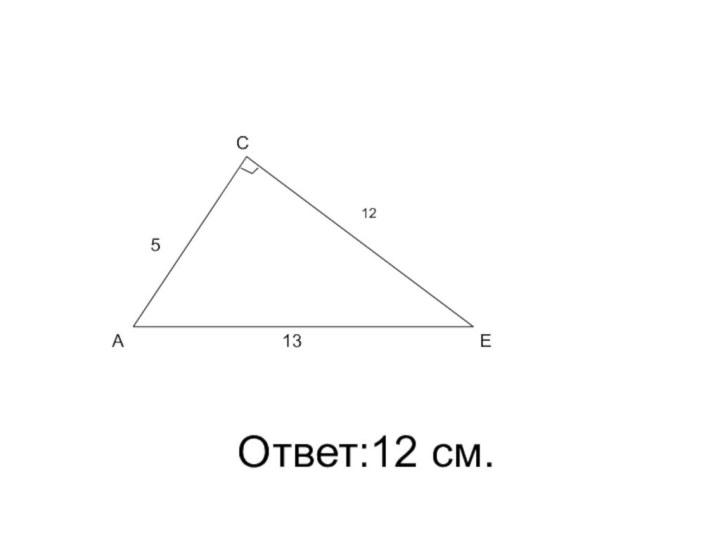
- 26. Ответ:12 см.AEC13512
- 27. Решение задач из учебника.
- 28. 1 вариант №483 (б) 2 вариант №484 (а)
- 29. Задача №486 (а)
- 30. Возможно ли было решение задач данного типа
- 31. Скачать презентацию
- 32. Похожие презентации
Тема урока:"Теорема Пифогора"





















Слайд 10
Пифагор
Пифагор Самосский
(около 570-около 500 до н.э.)
древнегреческий мыслитель,
религиозный политический деятель.
Пифагор 12 лет, пробыл в Вавилоне, общаясь
с магами, пока не вернулся на Самос в 56-летнем возрасте, где соотечественники признали его мудрым человекомВ популярной литературе иногда приписывают Пифагору Олимпийскую победу в боксе, путая Пифагора-философа с его тёзкой
Слайд 12
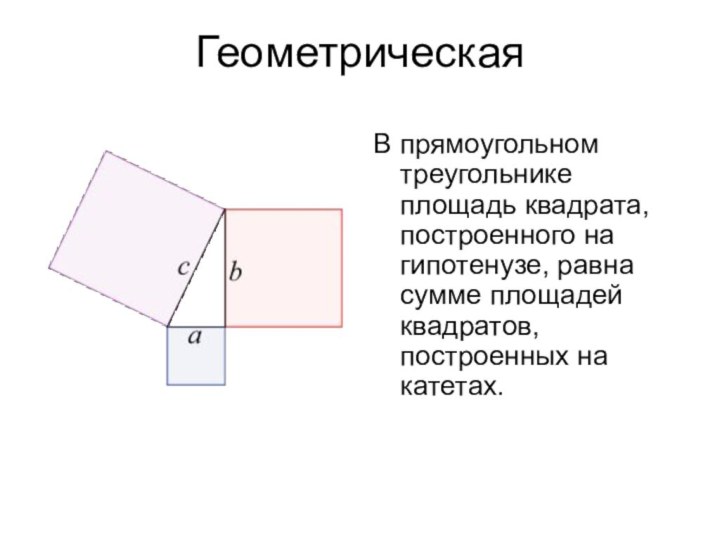
Геометрическая
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе,
равна сумме площадей квадратов, построенных на катетах.
Слайд 13
Алгебраическая
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов.
a²+b²=c²
АВ²=АС²+ВС²
А
в
С
с
а
b
Слайд 17
Доказательства
В научной литературе зафиксировано 367 доказательств данной теоремы.
Теорема Пифагора является единственной теоремой со столь внушительным числом
доказательств. Способы доказательства теоремы:
Через подобные треугольники.
Доказательство методом площадей.
Доказательство через равнодополняемость.
Доказательство через равносоставленность.
Доказательство Евклида.