Слайд 2
Геометрия – это не просто наука о свойствах
геометрических
фигур. Геометрия – это целый мир, который окружает
нас с
самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.
В качестве эпиграфа своего выступления я взяла слова известного математика Пойа:
«Лучше решить одну задачу несколькими способами,
чем несколько задач – одним»
Слайд 3
И это не случайно. Я хочу показать, что
при подготовке к экзаменам, необходимо отрабатывать умения решать задачи
именно так как сказал великий математик, т.е. решать задачи несколькими способами.
Начну с решения задачи из первой части.
Слайд 4
Задача 1.
Найдите длину отрезка АN, если радиус изображенной
на рисунке окружности ОК =3, АК = 2.
Решение.
1 способ.
АN – касательная к окружности, АМ – секущая. Если
из точки А к окружности проведены
касательная и секущая, то квадрат
отрезка касательной от точки А до
точки касания равен произведению
отрезков секущей от точки А до
точек пересечения секущей с
окружностью. АN2 = АК ∙ АМ = 2 ∙ 8 = 16
АN = 4.
Проведем радиус ОN. Касательная к
окружности перпендикулярна к радиусу,
проведенному в точку касания.
Значит, ∆АNО – прямоугольный.
АО = 5, NО = 3. По теореме Пифагора
3 способ
По основному тригонометрическому тождеству
Слайд 6
Задачи из второй части экзаменационной работы
Задача 2.
В трапеции
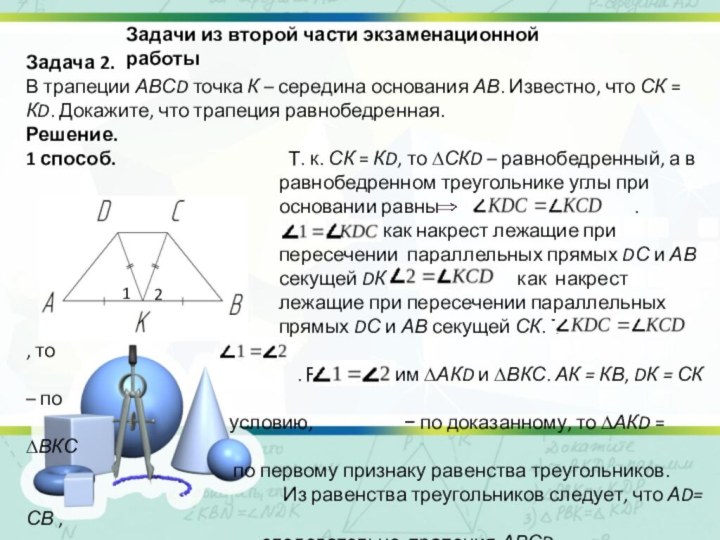
АВСD точка К – середина основания АВ. Известно, что
СК = КD. Докажите, что трапеция равнобедренная.
Решение.
1 способ. Т. к. СК = КD, то ∆СКD – равнобедренный, а в
равнобедренном треугольнике углы при
основании равны .
как накрест лежащие при
пересечении параллельных прямых DС и АВ
секущей DК, как накрест
лежащие при пересечении параллельных
прямых DС и АВ секущей СК. Т. к. , то
. Рассмотрим ∆АКD и ∆ВКС. АК = КВ, DК = СК – по
условию, − по доказанному, то ∆АКD = ∆ВКС
по первому признаку равенства треугольников.
Из равенства треугольников следует, что АD= СВ ,
следовательно трапеция АВСD – равнобедренная
.
Слайд 7
2 способ
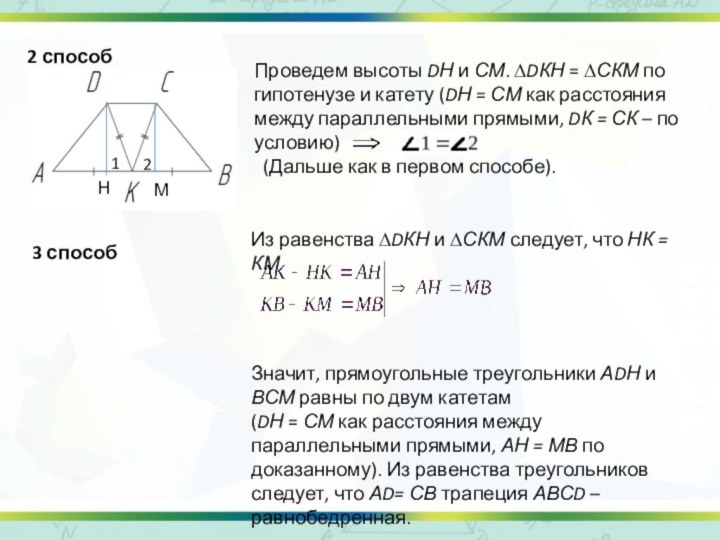
Проведем высоты DН и СМ. ∆DКН =
∆СКМ по гипотенузе и катету (DН = СМ как
расстояния между параллельными прямыми, DК = СК – по условию)
(Дальше как в первом способе).
Н
М
3 способ
Из равенства ∆DКН и ∆СКМ следует, что НК = КМ.
Значит, прямоугольные треугольники АDН и ВСМ равны по двум катетам
(DН = СМ как расстояния между параллельными прямыми, АН = МВ по доказанному). Из равенства треугольников следует, что АD= СВ трапеция АВСD – равнобедренная.
Слайд 8
Задача 3
В равнобедренном треугольнике АВС стороны АВ =
ВС = 10,
соs АВС =
. Найдите радиус окружности, вписанной в треугольник.
Решение.
1 способ.
По теореме косинусов
Радиус окружности, вписанной в треугольник, можно найти с помощью формулы . Площадь данного треугольника можно найти следующими способами: 1.
2. 3.
р =
Значит,
н
Слайд 9
Мы знаем, что центром окружности, вписанной в треугольник,
является точка пересечения его биссектрис. Проведем биссектрису ВН. Т.
к. в равнобедренном треугольнике высота, медиана и биссектриса, проведенные к основанию, совпадают, то биссектриса ВН будет и медианой, и высотой.
Из ∆АВН по теореме Пифагора .
2 способ
D
Проведем радиус ОD в точку касания. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Прямоугольные треугольники АВН и ОВD подобны по двум углам (угол АВН – общий, углы Н и D равны как прямые). В подобных треугольниках сходственные стороны пропорциональны.
Пусть ОН= х, тогда ВО = 8 – х.
х = 3. Значит, радиус НО = 3.
Слайд 10
3 способ
Начало такое же, как во 2-м способе.
Только рассмотрим не подобные треугольники, а прямоугольный треугольник ОВD.
Отрезки касательных к окружности, проведенные из одной точки, равны. Значит, АD = АН = 6. ВD = 10 – 6 = 4.
Пусть ОН = ОD = х, тогда ВО = 8 – х. По теореме Пифагора имеем уравнение:
Значит, радиус НО = 3.
4 способ
Проведем ВН (не будем проводить ОD, но точку касания D обозначим). Из второго способа
Из ∆АВН по теореме Пифагора
Отрезки касательных к окружности, проведенные из одной точки, равны. Значит, АD = АН = 6. ВD = 10 – 6 = 4.
По теореме о касательной и секущей ВD2 = ВМ ∙ ВН
16 = ВМ ∙ 8, ВМ = 2
МН = 2r = 8 – 2 = 6 r = 3. Значит, радиус НО = 3.
М
Слайд 11
5 способ
Проведем ВН и АО. Т.к. центром окружности,
вписанной в треугольник, является точка пересечения биссектрис, то АО
– биссектриса угла А, а значит, и биссектриса треугольника АВН. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Пусть ОН = х, тогда ВО = 8 – х.
16х = 48, х = 3. Значит, радиус НО = 3.
6 способ
Из ∆АВН: ВD = 4.
Из ∆ОВD: ОD = 3.
Значит, радиус НО = 3
Ответ: радиус вписанной окружности равен 3.
Слайд 12
Задача 4.
Основание AC равнобедренного треугольника ABC равно 12.
Окружность радиуса 8 с центром вне этого треугольника касается
продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Слайд 13
Решение.
1 способ.
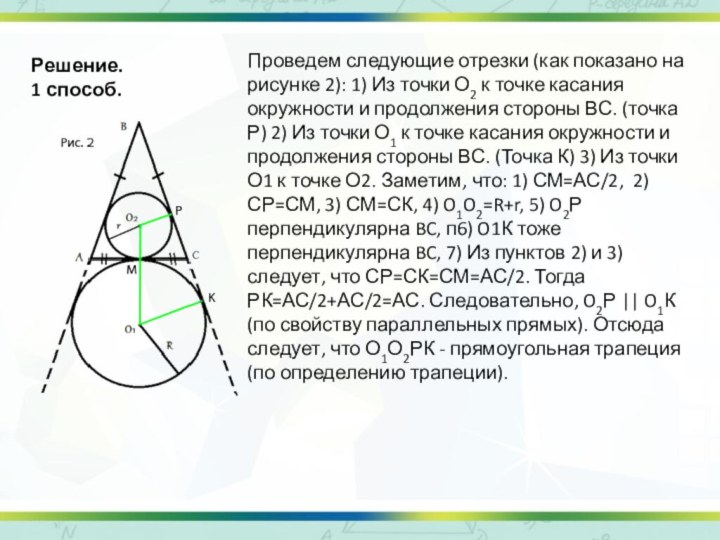
Проведем следующие отрезки (как показано на рисунке
2): 1) Из точки О2 к точке касания окружности
и продолжения стороны ВС. (точка Р) 2) Из точки О1 к точке касания окружности и продолжения стороны ВС. (Точка К) 3) Из точки О1 к точке О2. Заметим, что: 1) СМ=АС/2, 2) СР=СМ, 3) СМ=СК, 4) O1O2=R+r, 5) O2Р перпендикулярна BC, п6) O1К тоже перпендикулярна BC, 7) Из пунктов 2) и 3) следует, что СР=СК=СМ=АС/2. Тогда РК=АС/2+АС/2=АС. Следовательно, O2Р || O1К (по свойству параллельных прямых). Отсюда следует, что О1О2РК - прямоугольная трапеция (по определению трапеции).
Слайд 14
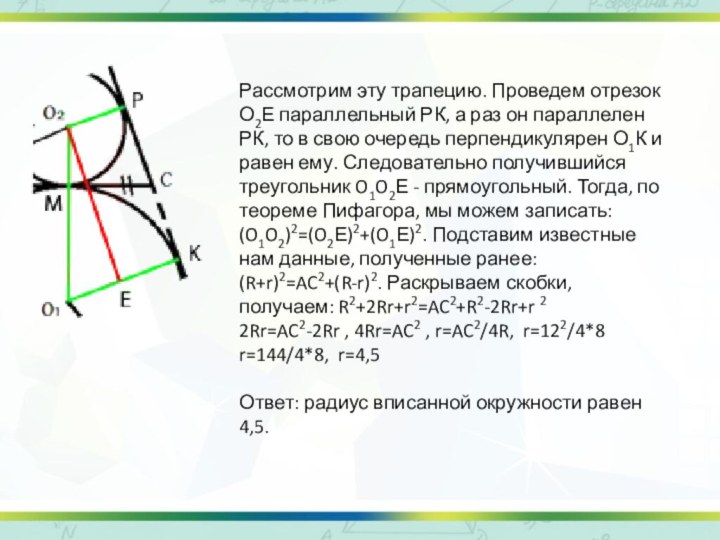
Рассмотрим эту трапецию. Проведем отрезок О2Е параллельный РК,
а раз он параллелен РК, то в свою очередь
перпендикулярен О1К и равен ему. Следовательно получившийся треугольник O1O2Е - прямоугольный. Тогда, по теореме Пифагора, мы можем записать: (O1O2)2=(O2Е)2+(O1Е)2. Подставим известные нам данные, полученные ранее: (R+r)2=AC2+(R-r)2. Раскрываем скобки, получаем: R2+2Rr+r2=AC2+R2-2Rr+r 2
2Rr=AC2-2Rr , 4Rr=AC2 , r=AC2/4R, r=122/4*8 r=144/4*8, r=4,5
Ответ: радиус вписанной окружности равен 4,5.
Слайд 15
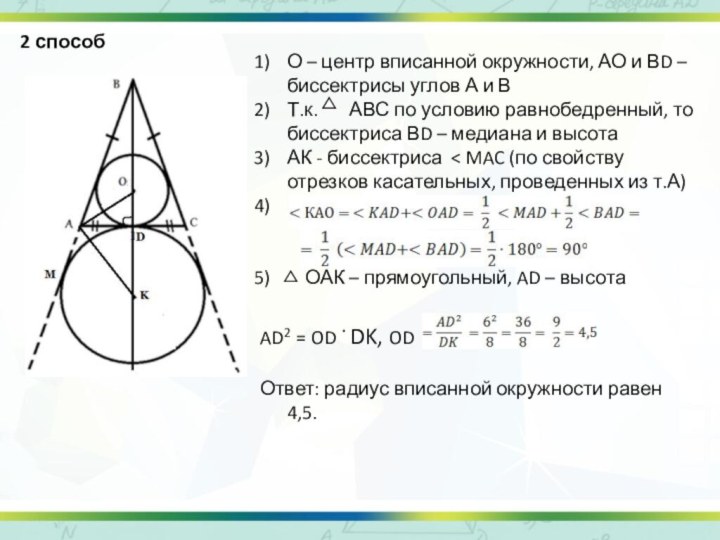
2 способ
О – центр вписанной окружности, АО и
ВD – биссектрисы углов А и В
Т.к.
АВС по условию равнобедренный, то биссектриса ВD – медиана и высота
АК - биссектриса < MAC (по свойству отрезков касательных, проведенных из т.А)
ОАК – прямоугольный, AD – высота
AD2 = OD . DK, OD
Ответ: радиус вписанной окружности равен 4,5.