- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение сечений многогранников
Содержание
- 2. Определение сечения. Секущей плоскостью многогранника назовем любую
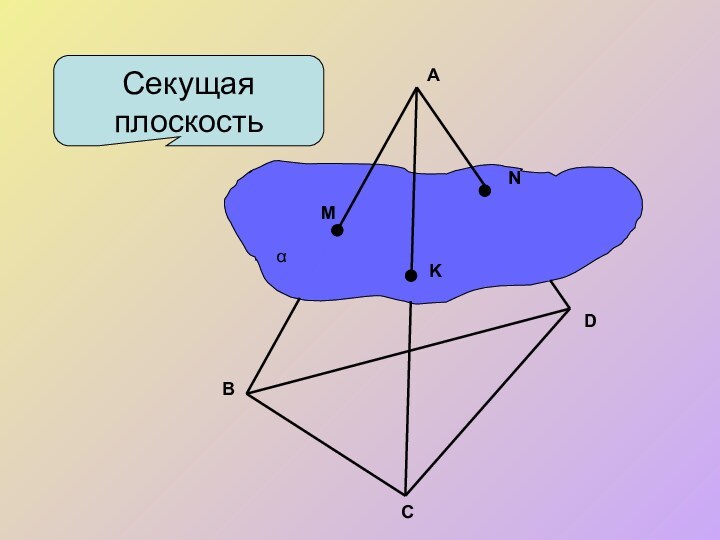
- 3. Секущая плоскостьАВСDMNKα
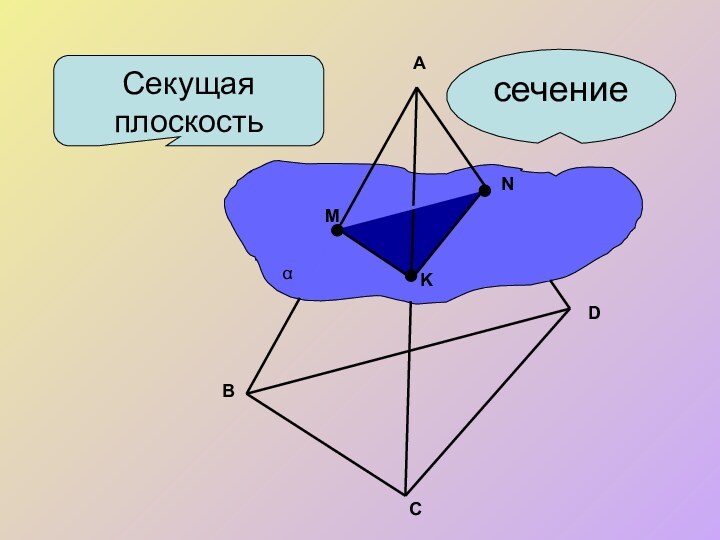
- 4. Секущая плоскостьсечениеABCDMNKα
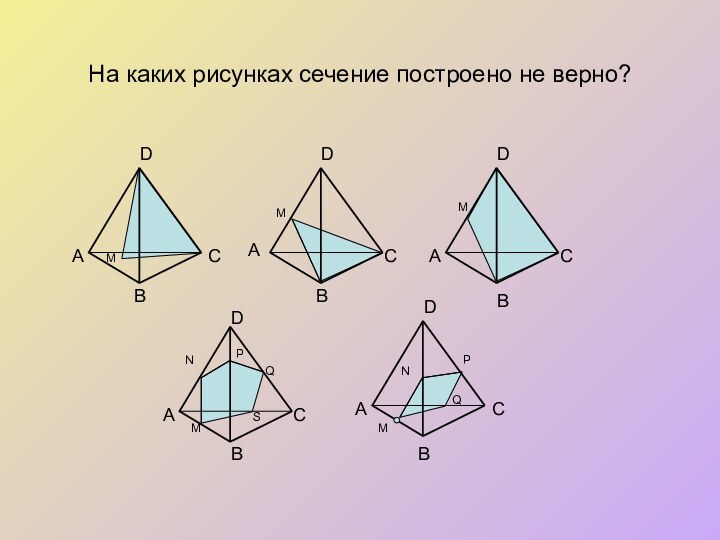
- 5. На каких рисунках сечение построено не верно? BАААААDDDDDBBBBCCCCCNMMMMMNQPPQS
- 6. PNПостроить сечение тетраэдра плоскостью, заданной тремя точками.
- 7. Построить сечение тетраэдра плоскостью, заданной тремя точками.Построение:АСВDNPQRE1.
- 8. Построить сечение тетраэдра плоскостью, заданной тремя точками.Построение:АBCDMNPXKSL1.
- 9. Аксиоматический метод
- 10. Постройте сечение пирамиды плоскостью, проходящей через
- 11. XY – след секущей плоскости
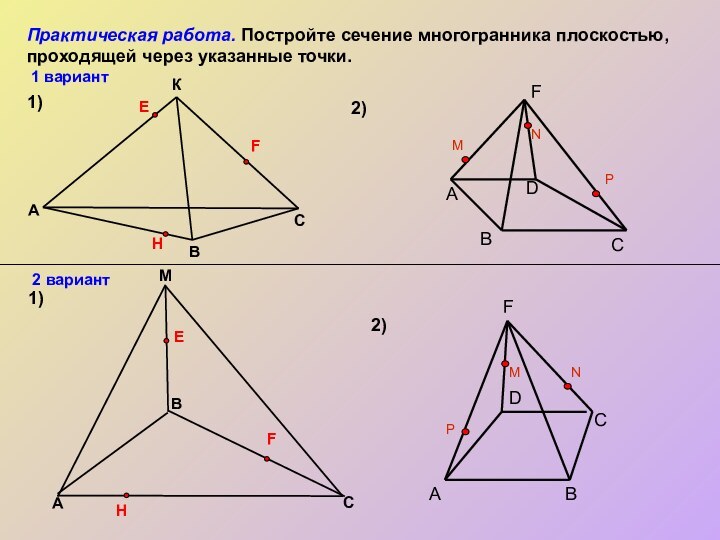
- 12. Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки.MA1)1)2)2)ВСКВAСEFHEHF1 вариант2 вариантDCBMNPАFDCBMNPАF
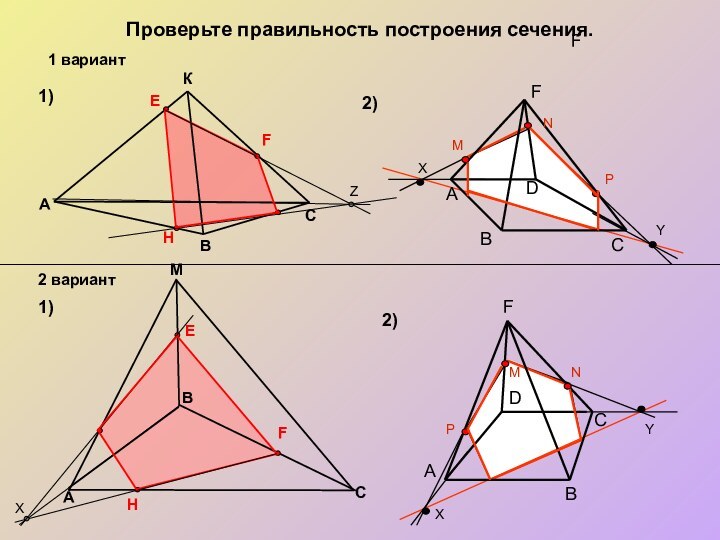
- 13. Проверьте правильность построения сечения. MA1)1)2)2)ВСКВAСEFHEHF1 вариант2 вариантDCBMNPАFFXYZXDCBMNPАFXY
- 14. Скачать презентацию
- 15. Похожие презентации
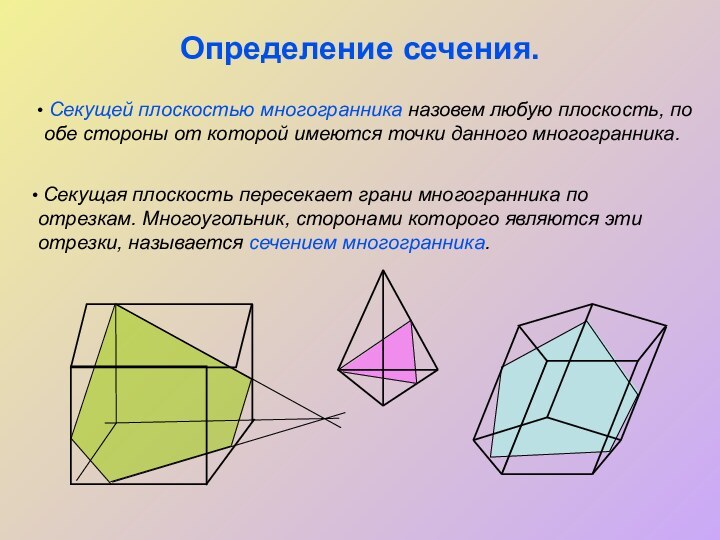
Определение сечения. Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Слайд 2
Определение сечения.
Секущей плоскостью многогранника назовем любую плоскость,
по обе стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Слайд 6
P
N
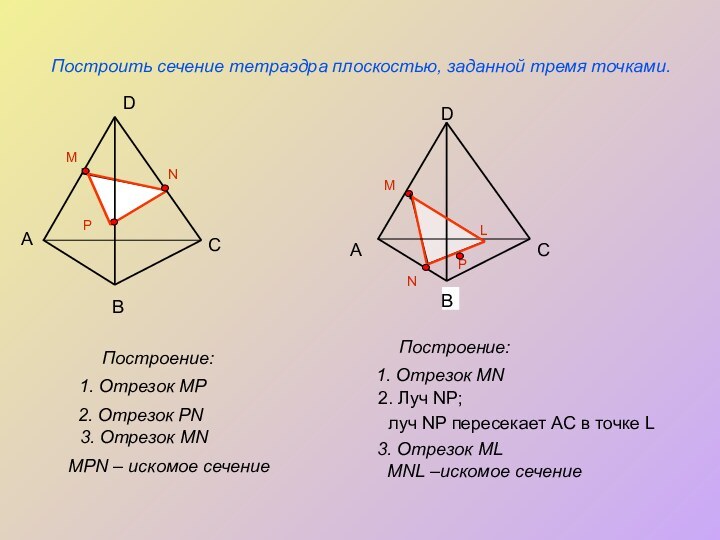
Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
В
С
D
P
M
N
2. Отрезок PN
А
В
С
D
M
L
1. Отрезок MP
Построение:
3.
Отрезок MNMPN – искомое сечение
1. Отрезок MN
2. Луч NP;
луч NP пересекает АС в точке L
3. Отрезок ML
MNL –искомое сечение
Слайд 7
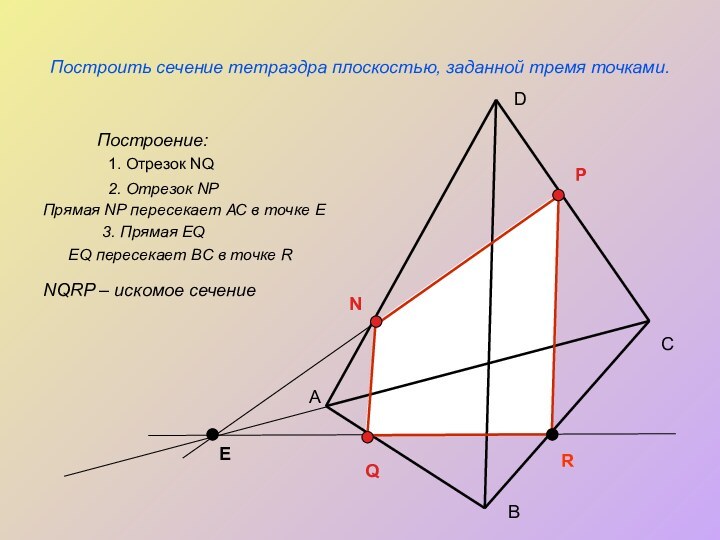
Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
С
В
D
N
P
Q
R
E
1. Отрезок
NQ
2. Отрезок NP
Прямая NP пересекает АС в точке
Е3. Прямая EQ
EQ пересекает BC в точке R
NQRP – искомое сечение
Слайд 8
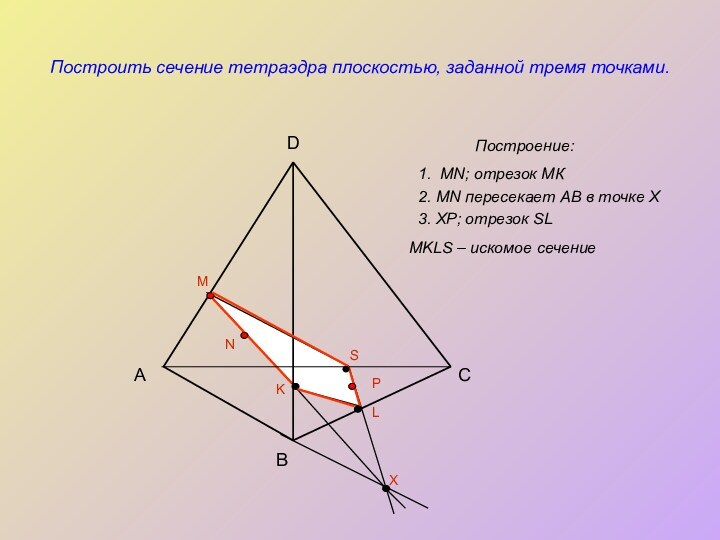
Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
B
C
D
M
N
P
X
K
S
L
1. MN;
отрезок МК
2. MN пересекает АВ в точке Х
3. ХР;
отрезок SLMKLS – искомое сечение
Слайд 9
Аксиоматический метод
Метод следов
Суть метода
заключается в построении вспомогательной прямой, являющейся изображением линии пересечения
секущей плоскости с плоскостью какой-либо грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры .
Слайд 10
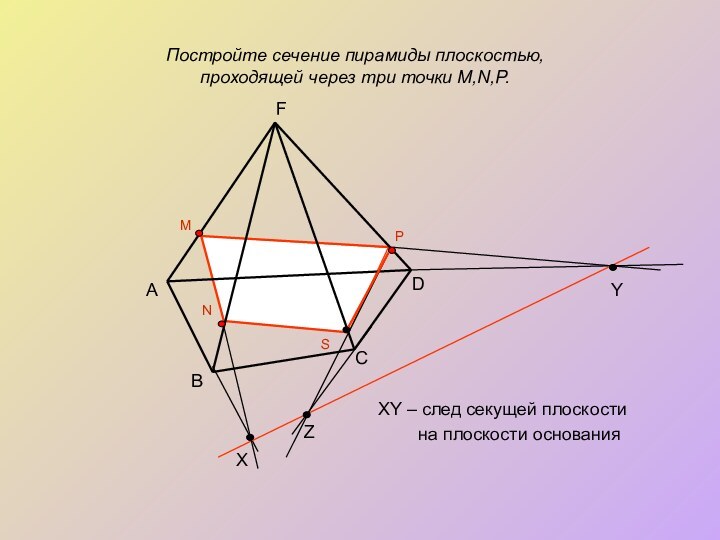
Постройте сечение пирамиды плоскостью,
проходящей через три точки
M,N,P.
XY – след секущей плоскости
на плоскости основанияD
C
B
А
Z
Y
X
M
N
P
S
F
Слайд 11
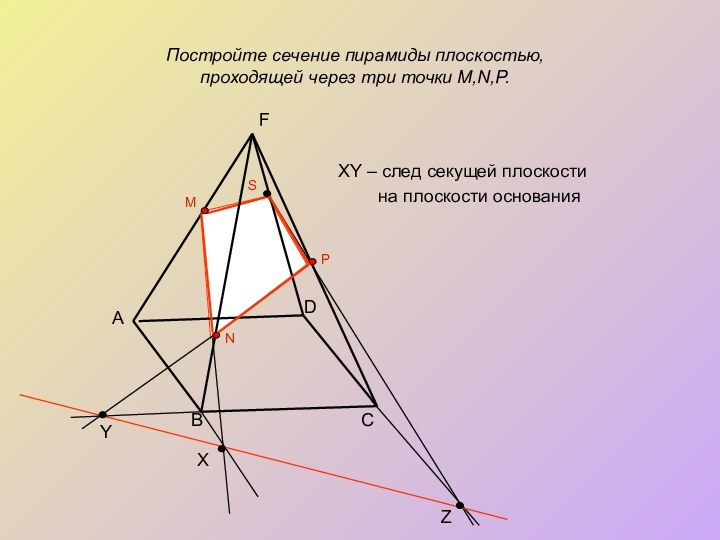
XY – след секущей плоскости
на плоскости основания
D
C
B
Z
Y
X
M
N
P
S
Постройте сечение пирамиды плоскостью,
проходящей через
три точки M,N,P.А
F