- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Геометрия архитектурной гармонии(9 класс)
Содержание
- 2. «Гармония является господствующей частью архитектуры»
- 3. Основные понятия«Архитектура»«Математическаягармония»«Золотое сечение»
- 4. Термин «золотое сечение» ввел в XVI
- 5. Понятие о золотом деленииввел в научный обиход
- 6. Отрезок можно разделить точкой С на две
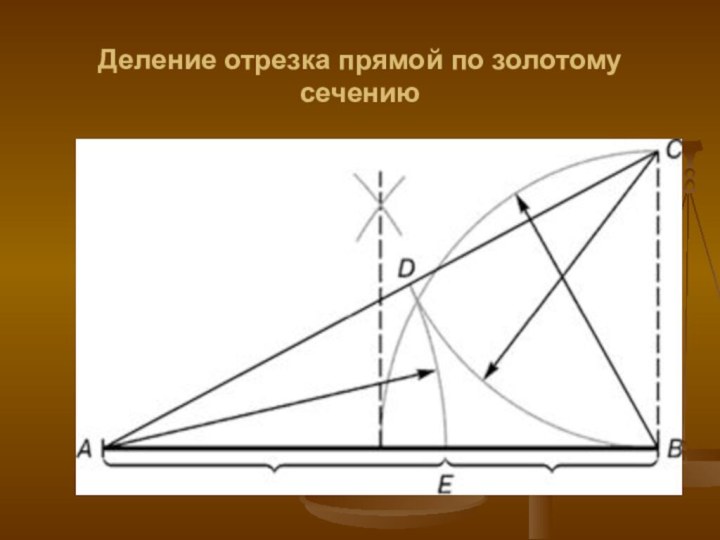
- 7. Деление отрезка прямой по золотому сечению
- 8. Исследования на уроках геометрии. Начертите на альбомном
- 9. Задание 2. Я предложил ученикам
- 10. Задание 3.Окружающие нас предметы дают примеры «золотого»
- 11. ПИРАМИДЫ –ОДНО ИЗ ЧУДЕС СВЕТАВсе на свете страшится времени,время страшится пирамид.Арабская пословица.
- 12. Пирамида фараона Хеопса. В истоках золотой
- 13. SMNADCB ∆ SMN является основным исходным элементом,
- 14. Длина
- 15. Прочность, польза, красота – формула архитектурного
- 16. В соотношениях многих частей Парфенона присутствует золотая
- 17. ГРЕЧЕСКИЙ ХРАМ БОГИНИ АРТЕМИДЫ
- 18. СОБОР НОТР-ДАМ ДЕ ПАРИ ВО
- 19. Пропорция – это математическая закономерность, прошедшая через
- 20. ЗДАНИЕ СЕНАТА
- 21. Известный русский архитектор М. Казаков в своем
- 22. ЕЩЕ ОДИН АРХИТЕКТУРНЫЙ ШЕДЕВР МОСКВЫ – ДОМ
- 24. АРХИТЕКТУРА СТУПИНО По фотографиям г. Ступино я
- 25. Дворец Культуры г, СтупиноАС DВАВ результате исследований
- 26. ВС:АС =1.65 Приближено к «золотому» сечению
- 27. Свято-троицкий Белопесоцкий монастырьМонастырь, расположенный на реке Ока,
- 28. Зимний Клуб.BADCЯ проверил , выполняется ли
- 29. Здание пенсионного фондаЗдание пенсионного фонда построено без
- 30. Ступинский многофункциональный центр
- 31. Я также проверил, соответствуют ли «золотому» сечению
- 32. В результате исследований объектов архитектуры города Ступино
- 33. В основном стандарты «Золотого» сечения» используются при строительстве или реставрации церквей и храмов.
- 35. Литература: 1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала
- 36. Скачать презентацию
- 37. Похожие презентации
«Гармония является господствующей частью архитектуры» В. Шеллинг



































Слайд 4
Термин «золотое сечение»
ввел в XVI веке
великий художник, ученый и изобретатель Леонардо да Винчи.
Слайд 5
Понятие о золотом делении
ввел в научный обиход
Пифагор, древнегреческий философ и математик (VI в. до н.э.)
Слайд 6
Отрезок можно разделить точкой С на две части
бесконечным множеством
способов, но говорят что точка С производит золотое
сечение отрезка АВ,если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка, т.е.
А С B
Деление отрезка
в «золотом» отношении
Слайд 8
Исследования на уроках геометрии.
Начертите на альбомном листе
любой прямоугольник, но желательно такой, какой вам больше нравится.
Найдите отношение ширины прямоугольника к его длине.Вывод: Результаты опыта среди учащихся 9 г класса показали, что у большинства отношение ширины к длине прямоугольника равно числу φ.
Задание 1.
Слайд 9
Задание 2.
Я предложил ученикам
класса отрезать от своего прямоугольника квадрат, сторона которого равна
меньшей стороне прямоугольника, и повторить вычисления. Мы снова получили золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, мы получали все меньшие и меньшие золотые прямоугольники
Слайд 10
Задание 3.
Окружающие нас предметы дают примеры «золотого» прямоугольника:
обложки многих книг, журналов, тетрадей, открытки, картины, крышки столов,
экраны телевизоров и т.д. близки по размерам к «золотому» прямоугольнику.Мы взяли наш учебник геометрии.
Нашли отношение ширины к длине.
Получившееся отношение φ =0,666...
«Золотой» прямоугольник.
Слайд 11
ПИРАМИДЫ –ОДНО ИЗ ЧУДЕС СВЕТА
Все на свете страшится
времени,
время страшится пирамид.
Арабская пословица.
Слайд 12
Пирамида фараона Хеопса
.
В истоках золотой пропорции лежат
пирамиды Древнего Египта – хранилища многих неразгаданных тайн, фантастические
фигуры из камня, устремленные к Солнцу.
Слайд 13
S
M
N
A
D
C
B
∆ SMN является основным исходным элементом, определяющим
главные пропорции пирамиды, в ее осевом сечении.
Отношение катетов
SM и MN равно отношению гипотенузы SN к катету SM. Причем SN: MN= φ.
Слайд 14
Длина грани
пирамиды в Гизе равна 783.3 фута (238.7 м), высота
пирамиды -484.4 фута (147.6 м). Длина грани, деленная на высоту, приводит к соотношениюφ =1.618.
Высота 484.4 фута соответствует 5813 дюймам (5-8-13) - это числа из последовательности Фибоначчи.
Конструкция пирамиды основана на пропорции
φ =1,618.
ПИРАМИДЫ В ЗОЛОТОМ СЕЧЕНИИ
Слайд 16
В соотношениях многих частей Парфенона присутствует золотая пропорция.
Говорят: «…у греческого храма нет размеров, у него есть
пропорции»Одним из красивейших
произведений
древнегреческой архитектуры
является Парфенон (V в. до н. э.).
Слайд 17 ГРЕЧЕСКИЙ ХРАМ БОГИНИ АРТЕМИДЫ в Эфесе -
третье чудо света
С
В
А
D
Проведя исследование
греческого храма богини Артемиды, я узнал, что отношение ширины храма к его высоте AB:DC= 1.65 .
Слайд 18
СОБОР НОТР-ДАМ ДЕ ПАРИ
ВО ФРАНЦИИ
В
A
D
С
Золотое сечение
видно и во Франции.
Собор Нотр -Дам де Пари
- самый величественный и самый популярный собор, памятник ранней готики .Отношение рёбер крыши слева и справа равно примерно DC:AB=0.65
Слайд 19 Пропорция – это математическая закономерность, прошедшая через душу
зодчего. Это поэзия числа и геометрии на архитектурном языке.
Слайд 20 ЗДАНИЕ СЕНАТА В
МОСКОВСКОМ КРЕМЛЕ
Не только в Зарубежных странах придерживались золотого сечения.
Здание сената в Московском Кремле сделано по всем стандартам золотого сечения , ведь отношение высоты крыла этого здания к его ширине равно DC:AB= 1.61 С
D
А
B
Слайд 21 Известный русский архитектор М. Казаков в своем творчестве
широко использовал “золотое» сечение
“Золотое» сечение можно обнаружить не только
в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова (Ленинский проспект, д. 5
Слайд 22
ЕЩЕ ОДИН АРХИТЕКТУРНЫЙ ШЕДЕВР МОСКВЫ – ДОМ ПАШКОВА
ОН ЯВЛЯЕТСЯ ОДНИМ ИЗ НАИБОЛЕЕ СОВЕРШЕННЫХ
ПРОИЗВЕДЕНИЙ АРХИТЕКТУРЫ В. БАЖЕНОВАНаружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г. AB:DC=1,6
А
D
С
B
Слайд 23
О своем
любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет
три предмета: красоту, спокойность и прочность здания... К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождем является рассудок”.
Слайд 24
АРХИТЕКТУРА СТУПИНО
По фотографиям г. Ступино я провел
математические расчеты с целью определения присутствия «золотого» сечения в
архитектуре данных культурных комплексов.
Слайд 25
Дворец Культуры г, Ступино
А
С
D
В
А
В результате исследований
выяснил,
что в соотношениях
многих частей
Дворца культуры
присутствует «золотая»
пропорция. Например отношение высоты колонны АВ к антаблементу ДС приблизительно равно AB:DC=1,6.
Слайд 26
ВС:АС =1.65
Приближено к «золотому» сечению
ЗДАНИЕ
ПО УЛ. АНДРОПОВА
Ступинская стоматологическая поликлинника
A
B
C
Слайд 27
Свято-троицкий Белопесоцкий монастырь
Монастырь, расположенный на реке Ока,
полностью построен с учетом стандартов «золотого» сечения.
Например: отношение
отрезков АВ:DC= 1.61A
C
B
D
Слайд 28
Зимний Клуб.
B
A
D
C
Я проверил , выполняется ли «золотая»
пропорция на примере кинотеатра «Зимнего клуба»:
отношение длины и высоты
арки перед входом в кинотеатр DC:АВ=2,2. «Золотого сечения я не обнаружил
Слайд 29
Здание пенсионного фонда
Здание пенсионного фонда построено без учета
законов «Золотого сечения». Отношение его длины к высоте
равно AB:DC=2.2A
B
D
C
Слайд 30
Ступинский многофункциональный центр (МФЦ)
Отношение длины карниза крыши к высоте до
нижней рамки примерно AB:DC=1,75.Здание МФЦ построено без учёта правил «золотого» сечения.
B
D
C
A
Слайд 31 Я также проверил, соответствуют ли «золотому» сечению ледовый
Дворец, цветочный магазин на бульваре Победы, многоэтажные дома, фонтан
Слайд 32
В результате исследований объектов архитектуры города Ступино пришел
к выводу, что не все рассматриваемые здания подчиняются
принципу «золотого» сечения. Многие здания, построенные в советское время и современные здания, формирующие лицо нашего города, тяготеют к законам красоты.
Слайд 33
В основном стандарты «Золотого» сечения» используются при строительстве
или реставрации церквей и храмов.
Слайд 34
ВЫВОД
Приобретенные нами знания о
золотых пропорциях убедили нас в том, Золотое сечение в архитектуре действительно является основополагающим принципом красоты, прочности, надежности.
Слайд 35
Литература:
1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в
школе», выпуск 7. Москва «Школа-Пресс», 1998год
2. А.В. Волошинов «Математика
и искусство», Москва, «Просвещение»,1992 ГОД3. Энциклопедический словарь юного математика Москва 1989 год.
4.А.В. Волошинов. Математика и искусство. М.: Просвещение. 2000.
5. И.М. Шевелёв, М.А. Марутаев, И.П. Шмелёв. Золотое сечение. М.: Стройиздат. 1990.
6. А.В. Иконников. Художественный язык архитектуры. М: Стройиздат. 1982.
7. http://www.zolotoe-sechenie.mn.ru
8.
9.
10. И.Ф.Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год.
11. DVD Tsarskoe selo Master Video, 2004
12. CD Microsoft Office at school