- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема невесты
Содержание
- 2. У математиков арабского Востока эта теорема получила
- 3. Пифагор-мыслитель, математик, философ.
- 4. Историческая справкаСуществует замечательное соотношение между гипотенузой и
- 5. Она была известна задолго
- 6. Пифагор 2523 года назад доказал теорему о
- 7. Сумма площадей квадратов, построенных на катетах прямоугольного
- 8. Картинка, иллюстрирующая теорему Пифагора, была ранее своеобразным
- 9. ВЕЛИКИЕ
- 10. Первая тайна заключается в таком множестве названий:
- 11. Вторая тайна – точно неустановленно количество доказательств
- 12. третья тайна – легенды о самом Пифагоре,
- 13. ОБЛАСТИ ПРИМЕНЕНИЯСтроительствоАстрономияМобильная связь
- 14. Теорема Пифагора всегда имела широкое применение
- 15. Мобильная связьКакую наибольшую высоту должна иметь антенна
- 16. В конце девятнадцатого века высказывались разнообразные предположения
- 17. 1.1 Мозаика «Квадрат, построенный на гипотенузе прямоугольного треугольника,
- 18. Дерево Пифагора— разновидность основанная на фигуре, известной
- 19. Одним из свойств дерева Пифагора является то,
- 20. Обдуваемое ветром дерево Пифагора
- 21. 1.2 Древнекитайское доказательство Математические
- 22. 1.3 Древнеиндийское доказательство Древней Индии заметили, что для
- 23. 1.4 Доказательство Евклида Доказательство Евклида приведено в предложении
- 24. Пусть ABC — данный прямоугольный с треугольник с прямым
- 26. Пифагор Самосский
- 27. «Теорема Пифагора. Эллас. 350 драхм».
- 28. Скачать презентацию
- 29. Похожие презентации
У математиков арабского Востока эта теорема получила название «теорема невесты» за сходство чертежа с бабочкой, что по-гречески называлось «нимфой». При переводе с греческого арабский переводчик, не обратив внимание на чертеж перевел слово «нимфа» как «невеста», а


























Слайд 4
Историческая справка
Существует замечательное соотношение между гипотенузой и катетами
прямоугольного треугольника, справедливость которого была доказана древнегреческим философом и
математиком Пифагором ( VI в. до н. э.).Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора.
Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.
Слайд 5
Она была известна задолго до
Пифагора. За 8 веков до н. э. эта теорема
была хорошо известна индийцам под названием «Правила веревки» и использовалась ими для построения алтарей, которые по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта.Теорема Пифагора имеет богатую историю.
Пифагор, не открыл эту теорему, а нашел ее доказательство, хотя доказательство самого Пифагора до нас не дошло.
Значение теоремы состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии и решить множество задач.
Слайд 6 Пифагор 2523 года назад доказал теорему о том,
что квадрат гипотенузы равен сумме квадратов катетов, соответствующий чертеж
был похож на штаны, но сам автор не обратил на это внимания т.к. в то время этот предмет не был еще изобретен и он сам ходил без штанов. ОДНАКО, в 1887 году после рождества христова, одна петербургская гимназистка, сильно интересовавшаяся штанами обратила на это внимание и в порыве энтузиазма дала новую формулировку старой теоремы "Пифагоровы штаны во все стороны равны".Слайд 7 Сумма площадей квадратов, построенных на катетах прямоугольного треугольника,
равна площади квадрата, построенного на его гипотенузе Именно так
выглядела классическая формулировка теоремы.
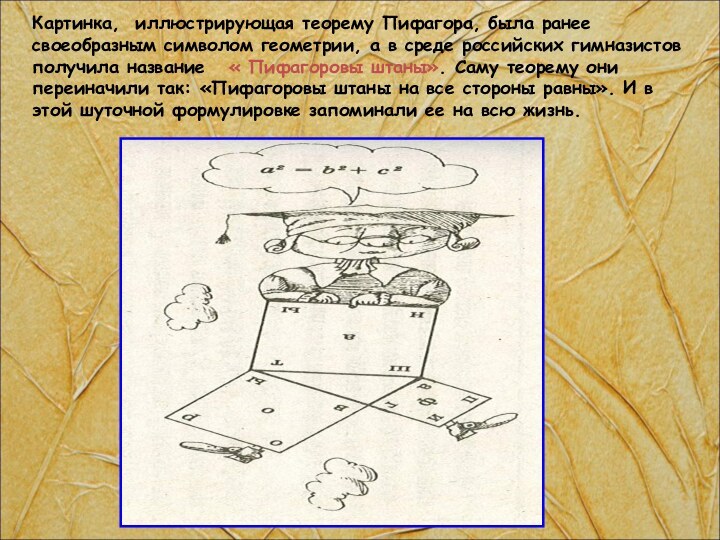
Слайд 8 Картинка, иллюстрирующая теорему Пифагора, была ранее своеобразным символом
геометрии, а в среде российских гимназистов получила название
« Пифагоровы штаны». Саму теорему они переиначили так: «Пифагоровы штаны на все стороны равны». И в этой шуточной формулировке запоминали ее на всю жизнь.Слайд 10 Первая тайна заключается в таком множестве названий: «теорема
бабочки», «т. невесты», «т. нимфы», « т. 100 быков»,
«бегство убогих», «мост ослов», «ветряная мельница». Думаю, что не найти другой теоремы, которая имела бы столько всевозможных названий!Слайд 11 Вторая тайна – точно неустановленно количество доказательств знаменитой
теоремы Пифагора. Существует более 350 доказательств этой теоремы, поэтому
она даже попала в Книгу рекордов Гиннеса! Но, конечно же, принципиально различных идей в этих доказательствах используется сравнительно немного.Слайд 12 третья тайна – легенды о самом Пифагоре, человеке,
который первым доказал эту теорему. Существует легенда, что когда
Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков. Также о гипнотических способностях учёного ходили легенды: будто он одним своим взглядом мог менять направление полёта птиц. А ещё рассказывали, что этого удивительного человека одновременно видели в разных городах, между которыми было несколько дней пути. И что ему якобы принадлежало «колесо фортуны», вращая которое, он не только предсказывал будущее, но и вмешивался, если это было необходимо, в ход событий.Слайд 14 Теорема Пифагора всегда имела широкое применение при решении
самых разнообразных геометрических задач. В зданиях готического и романского
стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон
Слайд 15
Мобильная связь
Какую наибольшую высоту должна иметь антенна мобильного
оператора, чтобы передачу можно было принимать в радиусе R=200
км? (радиус Земли равен 6380 км.)Решение:
Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB=OA+AB OB=r + x.
Используя теорему Пифагора, получим Ответ: 2,3 км.
Слайд 16 В конце девятнадцатого века высказывались разнообразные предположения о
существовании обитателей Марса подобных человеку. В шутку, хотя и
не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
Слайд 17
1.1 Мозаика
«Квадрат, построенный на гипотенузе
прямоугольного треугольника, равновелик
сумме квадратов, построенных на его катетах».
Простейшее доказательство теоремы
получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. Достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников {рис. 1), чтобы убедиться в справедливости теоремы. Например, для A ABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два. Теорема доказана.Слайд 18 Дерево Пифагора— разновидность основанная на фигуре, известной как
«Пифагоровы штаны».
ПифагорПифагор, доказывая свою знаменитую теоремуПифагор, доказывая свою знаменитую
теорему, построил фигуруПифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман (1891Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман (1891—1961Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку.Слайд 19 Одним из свойств дерева Пифагора является то, что,
если площадь первого квадрата равна единице, то на каждом
уровне сумма площадей квадратов тоже будет равна единице.Классическое дерево Пифагора
Слайд 21
1.2 Древнекитайское доказательство
Математические трактаты
Древнего Китая дошли до нас в редакции II в.
до н.э. Дело в том, что в 213 г. до н.э. китайский император Ши Хуанди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг. Так возникла тематика в девяти книгах» — главное из сохранившихся математике — астрономических сочинений в книге «Математики» помещен чертеж ,доказывающий теорему Пифагора. Ключ к этому доказательству подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, Ъ и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний — квадрат со стороной с, построенный на гипотенузе .Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника ,то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой — а2+Ь2, т.е. с2=а2+Ь2. Теорема доказана. При таком доказательстве построения внутри квадрата на гипотенузе, которые видны на древнекитайском чертеже ,не используются. По-видимому, древнекитайские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника отрезать и приложить гипотенузами к двум другим гипотенузам ,то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и Ь, т.е. с2=а2+Ь2.
Слайд 22
1.3 Древнеиндийское доказательство
Древней Индии заметили, что для доказательства
теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В
написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен чертеж с характерным для индийских доказательств, словом «смотри!». Как видим, прямоугольные треугольники уложены здесь гипотенузой наружу и квадрат с 2 перекладывается в «кресло невесты» а*a-b*b .Заметим, что частные случаи теоремы Пифагора (например, построение квадрата, площадь которого вдвое больше площади данного квадрата) встречаются в древнеиндийском трактате «Сульва сутра» (VII-V вв. до н.э.).
Слайд 23
1.4 Доказательство Евклида
Доказательство Евклида приведено в предложении 47
первой книги «Начал». На гипотенузе и катетах прямоугольного треугольника
ABC строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник ICEL — квадрату АС КС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе. В самом деле, затушеванные на рисунке треугольники ABD и BFC равны по двум сторонам и углу между ними: FB=AB, BC=BD и ∠FBC=d+∠ABC=∠ABD. Но SABD = 1/2 SBJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=l/2 SABFH (BF — общее основание, АВ — общая высота). Отсюда учитывая, что SABD=SFBC, имеем SBJLD= SABFH. Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что SiCEL=SACKG. Итак, SABFH+SACKG=SBJLD+SJCEL= SBCED, что и требовалось доказать. Доказательство Евклида в сравнении древнекитайским или древнеиндийским выглядит чрезмерно сложным. По этой причине его нередко называли «ходульным» и «надуманным». Но такое мнение поверхностно. Теорема Пифагора у Евклида является заключительным звеном в цепи предложений 1-й книги «Начал». Для того чтобы логически безупречно построить эту цепь, чтобы каждый шаг доказательства был основан на ранее доказанных предложениях, Евклиду нужен был именно выбранный им путь.
Слайд 24
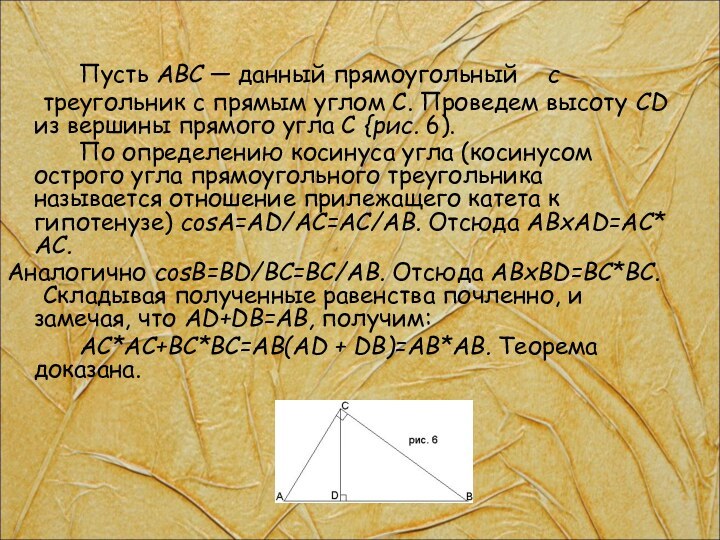
Пусть ABC — данный прямоугольный с
треугольник с прямым углом
С. Проведем высоту CD из вершины прямого угла С
{рис. 6).По определению косинуса угла (косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе) cosA=AD/AC=AC/AB. Отсюда ABxAD=AC* AC.
Аналогично cosB=BD/BC=BC/AB. Отсюда ABxBD=BC*BC. Складывая полученные равенства почленно, и замечая, что AD+DB=AB, получим:
AC*AC+BC*BC=AB(AD + DB)=AB*AB. Теорема доказана.