- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Аксиома параллельных прямых 7 кл.
Содержание
- 2. Совершенствование навыков решения задач на применение признаков параллельности прямых№ 202Дано:
- 3. Совершенствование навыков решения задач на применение признаков параллельности прямых№ 3Дано:
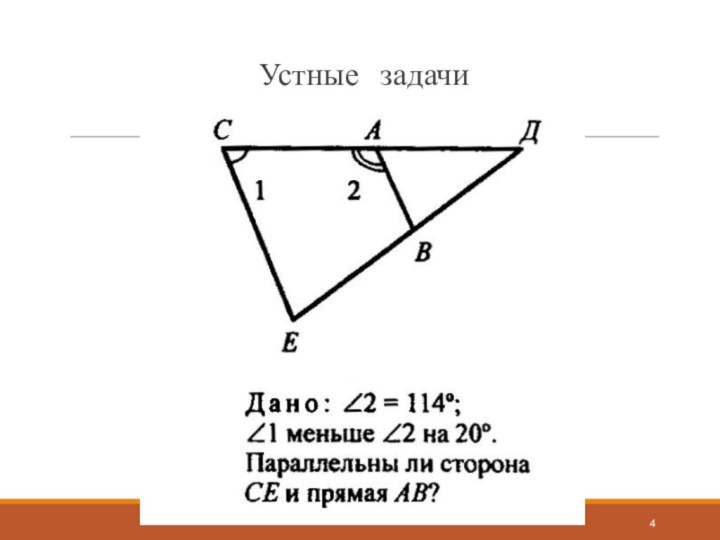
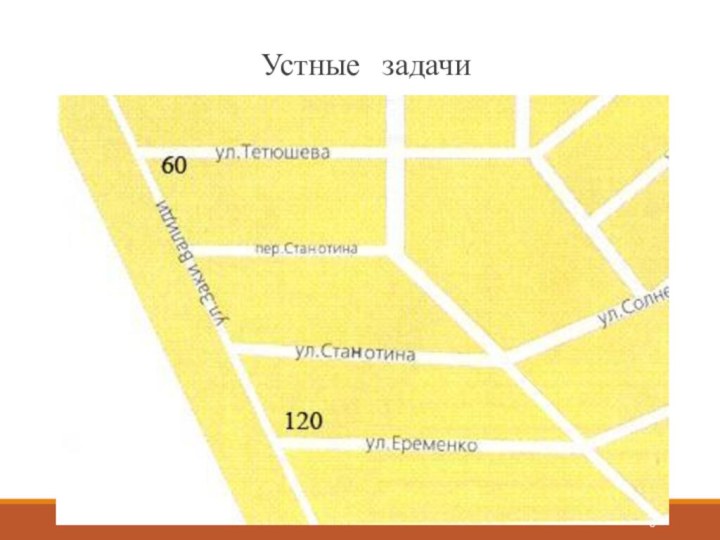
- 4. Устные задачи
- 5. Устные задачи
- 6. Аксио́ма – исходное утверждение, принимаемое истинным
- 7. Аксиомы ЕвклидаОт всякой точки до всякой точки
- 8. МbaАксиома параллельных прямыхчерез точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
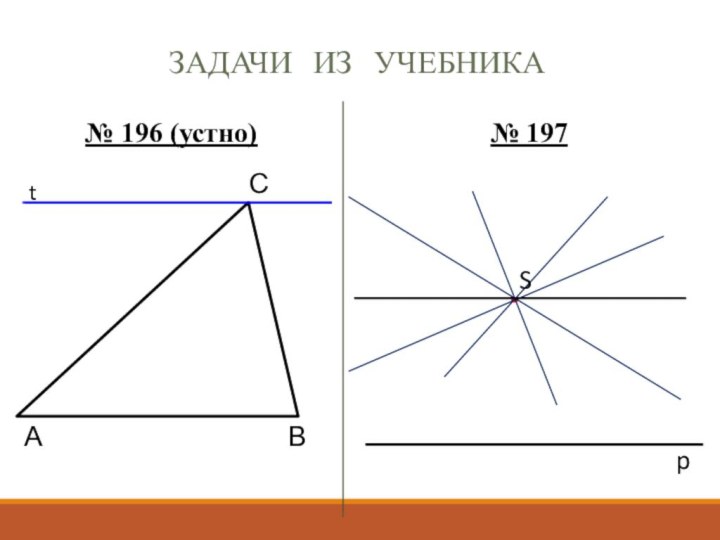
- 9. Задачи из учебника№ 196 (устно)АВСt№ 197pS
- 10. I Если прямая пересекает одну из двух
- 11. IIЕсли две прямые параллельны третьей прямой, то
- 12. № 198abpcKN1. a ıı b2. с пересекает
- 13. № 199АВСрСВ пересекает АВ, значит пересекает и
- 14. Отметить знаком «+» правильные утверждения
- 15. Проверочная работаВариант 11. «-»2. «-»3. «-»4. «+»5. «+»Вариант 21. «+»2. «+»3. «-»4. «-»5. «+»
- 16. Скачать презентацию
- 17. Похожие презентации










Слайд 3 Совершенствование навыков решения задач на применение признаков параллельности
прямых
№ 3
Дано:
и b?Слайд 6 Аксио́ма – исходное утверждение, принимаемое истинным без
доказательств, и которое в последующем служит «фундаментом» для построения
какой-либо теории, дисциплины.Теоре́ма – утверждение , для которого в рассматриваемой теории существует доказательство.
Следствие – утверждение, которое выводится из теорем и аксиом.
Аксиома, теорема и следствие:
Слайд 7
Аксиомы Евклида
От всякой точки до всякой точки можно
провести прямую.
Ограниченную прямую можно непрерывно продолжать по прямой.
Из всякого центра и всяким раствором может быть описан круг.
Все прямые углы равны между собой.
Если прямая, падающая на две прямые, образует внутренние односторонние углы, в сумме меньшие двух прямых, то продолженные неограниченно, эти две прямые встретятся с той стороны, где углы в сумме меньше двух прямых.
Слайд 8
М
b
a
Аксиома параллельных прямых
через точку, не лежащую на данной
прямой, проходит только одна прямая, параллельная данной
Слайд 10
I
Если прямая пересекает одну из двух параллельных
прямых, то она пересекает и другую.
М
b
a
c
N
Следствия из
Аксиомы параллельных прямых
Слайд 11
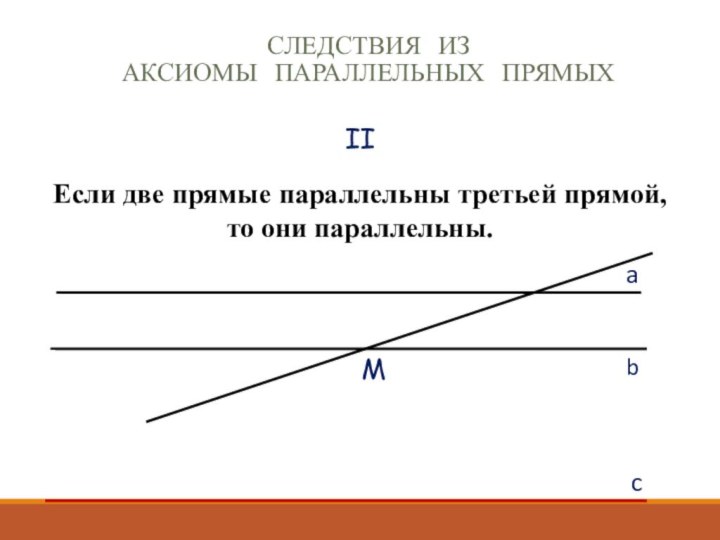
II
Если две прямые параллельны третьей прямой, то они
параллельны.
c
b
a
M
Следствия из
Аксиомы параллельных прямых
Слайд 12
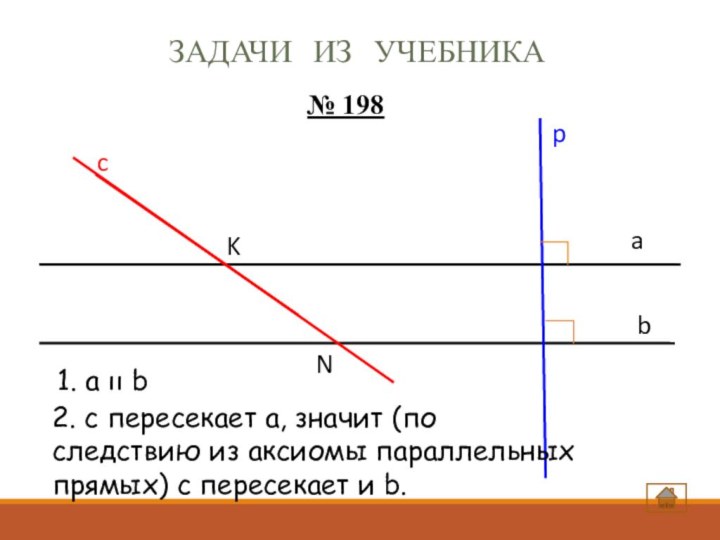
№ 198
a
b
p
c
K
N
1. a ıı b
2. с пересекает а,
значит (по следствию из аксиомы параллельных прямых) с пересекает
и b.Задачи из учебника
Слайд 13
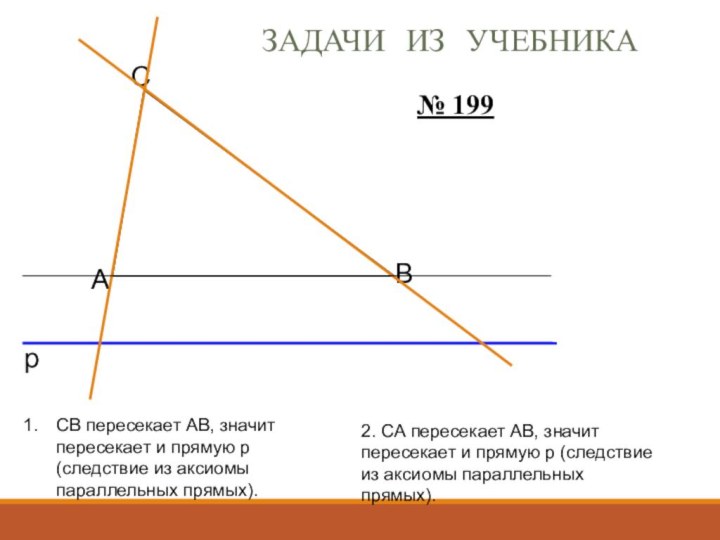
№ 199
А
В
С
р
СВ пересекает АВ, значит пересекает и прямую
р (следствие из аксиомы параллельных прямых).
2. СА пересекает АВ,
значит пересекает и прямую р (следствие из аксиомы параллельных прямых).Задачи из учебника
Слайд 14 Отметить знаком «+» правильные утверждения
и знаком
«-» - ошибочные.Вариант 1
1. Аксиомой называется
математическое утверждение о свойствах геометрических фигур, требующее доказательства.
2. Через любые две точки проходит прямая.
3. На любом луче от начала можно отложить отрезки, равные данному, причем сколько угодно много.
4.Через точку не лежащую на
данной прямой, проходит только одна прямая, параллельная данной.
5. Если две прямые параллельны третьей, то они параллельны между собой.
Вариант 2
1. Аксиомой называется
математическое утверждение о
свойствах геометрических фигур,
принимаемое без доказательства.
2. Через любые две точки проходит
прямая, и притом только одна.
3. Через точку, не лежащую на
данной прямой, проходят только
две прямые, параллельные
данной.
4. Если прямая пересекает одну из
двух параллельных прямых, то она
перпендикулярна другой прямой.
5. Если прямая пересекает одну из
двух параллельных прямых, то она
пересекает и другую.
Проверочная работа





























