- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тригонометрические формулы
Содержание
- 2. Цель урока Повторить и систематизировать изученный материалПодготовиться к контрольной работе
- 3. Задачи урокаПовторить определение синуса, косинуса, тангенса, котангенса
- 4. Ход урокаБлиц-опросЗакрепление знаний и уменийСамостоятельная работа (тест) Проверка самостоятельной работыЭто интересноИтог урока Домашнее задание
- 5. Блиц-опросСинусом угла α называется _____ точки, полученной
- 6. Блиц-опросСинусом угла α называется ордината точки, полученной
- 7. Оценка«5» - 12«4» - 10 – 11«3» - 7 – 9«2» - 0 – 6
- 8. Закрепление знаний и умений№546 1) дано: найти: ОТВЕТ: 3) дано: найти: ОТВЕТ:
- 9. Упростить выражениеОтвет: -2Ответ:1.2.
- 10. №555 1) Доказать:№557 Упростить выражение ОТВЕТ: № 564 1) Доказать:
- 11. вариант 11) Найдите значениеа) -2,5; б)
- 12. Проверка 1 вариант г) б) г) б) 2 вариант б) в) г) а)
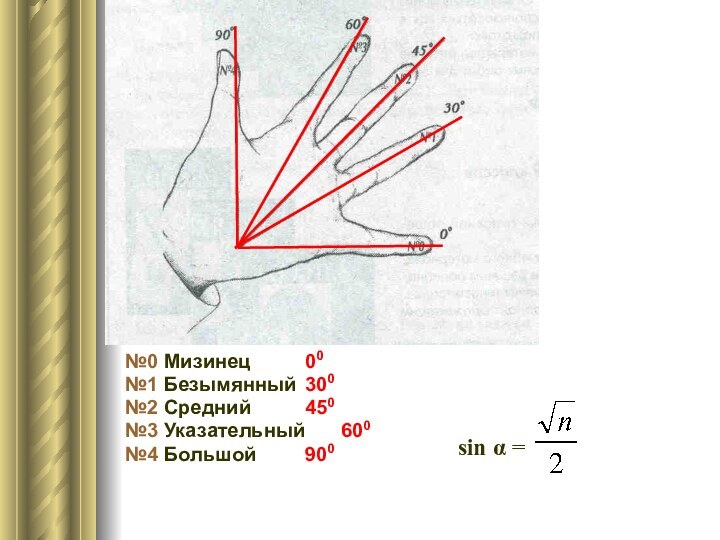
- 13. Это интересноТригонометрия в ладони
- 14. Зарождение тригонометрии относится к глубокой древности. Само
- 15. №0 Мизинец 00№1 Безымянный 300№2 Средний 450№3 Указательный 600№4 Большой 900
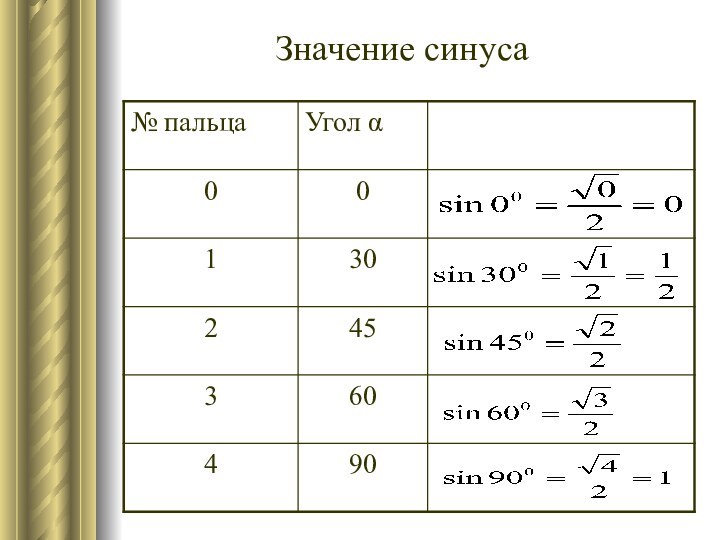
- 16. Значение синуса
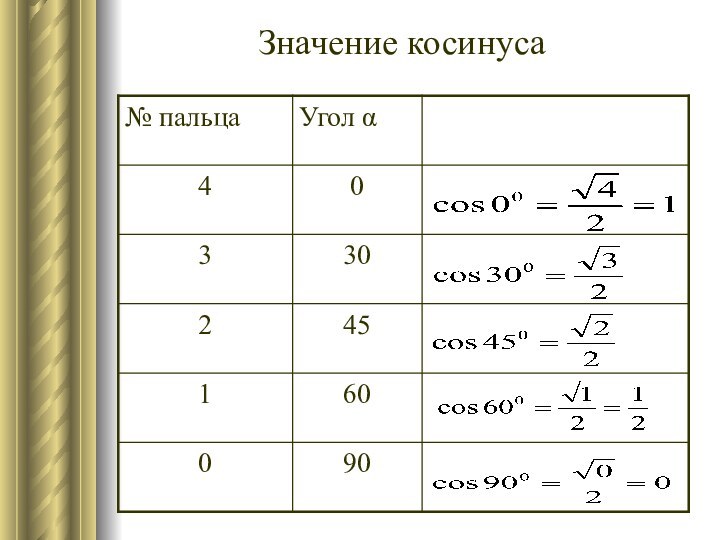
- 17. Значение косинуса
- 18. Домашнее заданиеПроверь себя стр. 166
- 19. Скачать презентацию
- 20. Похожие презентации
















Слайд 2
Цель урока
Повторить и систематизировать изученный материал
Подготовиться к контрольной
работе
Слайд 3
Задачи урока
Повторить определение синуса, косинуса, тангенса, котангенса числа
α;
Повторить формулы приведения, формулы двойного угла, формулы сложения;
Повторить основное
тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.Научить применять полученные знания при решении задач.
Слайд 4
Ход урока
Блиц-опрос
Закрепление знаний и умений
Самостоятельная работа (тест)
Проверка
самостоятельной работы
Это интересно
Итог урока
Домашнее задание
Слайд 5
Блиц-опрос
Синусом угла α называется _____ точки, полученной поворотом
точки______ вокруг начала координат на угол α
tg α
=sin2 α +cos2 α=
1+ tg2 α=
sin(-α)=
tg (-α) =
cos (α+β)=
sin (α-β)=
sin 2α=
tg (α+β)=
sin(π- α)=
cos ( + α)=
Косинусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
ctg α=
tg α∙ ctg α=
1+ ctg2 α=
cos (-α)=
ctg (-α) =
cos (α-β)=
sin (α+β)=
cos 2α=
tg 2α=
cos(π- α)=
sin ( + α)=
Слайд 6
Блиц-опрос
Синусом угла α называется ордината точки, полученной поворотом
точки (1;0) вокруг начала координат на угол α
tg
α =sin2 α +cos2 α = 1
1+ tg2 α =
sin(-α) = - sin α
tg (-α) = -tg α
cos (α+β) = cosα cosβ – sinα sinβ
sin (α-β) = sinα cosβ - cosα sinβ
sin 2α = 2sin αcos α
tg (α+β) =
sin(π- α) =sin α
cos ( + α) = -sinα
Косинусом угла α называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол α
ctg α=
tg α∙ ctg α = 1
1+ ctg2 α=
cos (-α) = cos α
ctg (-α) = -ctg α
cos (α-β)=cosα cosβ +sinα sinβ
sin (α+β)= sinα cosβ + cosα sinβ
cos 2α=cos2 α-sin2 α
tg 2α=
cos(π- α)= - cos α
sin ( + α)=-cos α
Слайд 11
вариант 1
1) Найдите значение
а) -2,5; б) 5,5; в)
-4,75; г) 3,25.
2) Дано:
Найдите значение:
а) ;б)
; в) ; г) . 3) Упростите выражение:
а) ;б) ;в) ;г) .
4) Упростите выражение:
а) ;б) ;
в) ;г)
вариант 2
1) Найдите значение
а) -3,5; б) 9,5; в) -0,5; г) 6,5.
2) Дано:
Найдите значение:
а) ; б) ; в) ; г)
3) Упростите выражение:
а) ; б) ;в) ;г)
4) Упростите выражение:
а) ; б) ;
в) ; г) .
Слайд 14 Зарождение тригонометрии относится к глубокой древности. Само название
«тригонометрия» греческого происхождения, обозначающее «измерение треугольников».
Гиппарх является автором
первых тригонометрических таблиц и одним из основоположников астрономии. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх (Hípparchos) (около 180—190 до н. э., Никея, — 125 до н. э., Родос), древнегреческий учёный.