Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Теорема о трех перпендикулярах (10 класс)

Содержание

Если две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна. aРасстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися
Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори, Мурманской Если две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую АНП-РМПовторение. Теорема о трех перпендикулярах.Прямая, проведенная в плоскости через основание наклонной перпендикулярно АНП-РМПовторение. Обратная теорема.Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, П-я 1АВИз точки М проведен перпендикуляр МВ к плоскости прямоугольника АВСD. Докажите, П-я 1DАЧерез вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная к плоскости ВЧерез вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его плоскости. ВЧерез вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его плоскости. Прямая ОК перпендикулярна к плоскости ромба АВСD, диагонали которого пересекаются в точке ВМАD№158.С60025 см П-РУглом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к Найти угол между наклонными и плоскостью (описать алгоритм построения). П-я Прямая ВD перпендикулярна к плоскости треугольника АВС. Известно, что ВD = Если прямая перпендикулярна к плоскости, то ее проекцией на эту плоскость является Если прямая параллельна плоскости, то ее проекцией на плоскость является прямая, параллельная AOИз точки А, удаленной от плоскости на расстояние d, проведены к
Слайды презентации

Слайд 2
Если две прямые скрещиваются, то через каждую из

Если две прямые скрещиваются, то через каждую из них проходит плоскость,

них проходит плоскость, параллельная другой прямой, и притом только

одна.

a

Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

b

Слайд 3 Расстояние между одной из скрещивающихся прямых и плоскостью,

Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую

проходящей через другую прямую параллельно первой, называется расстоянием между

скрещивающимися прямыми.



Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к этим прямым, называется их общим перпендикуляром.
На рисунке АВ – общий перпендикуляр.




Слайд 4 А
Н
П-Р


М

Повторение. Теорема о трех перпендикулярах.
Прямая, проведенная в плоскости

АНП-РМПовторение. Теорема о трех перпендикулярах.Прямая, проведенная в плоскости через основание наклонной

через основание наклонной перпендикулярно к ее проекции на эту

плоскость, перпендикулярна и к самой наклонной.

Н-я




Слайд 5 А
Н
П-Р


М

Повторение. Обратная теорема.
Прямая, проведенная в плоскости через основание

АНП-РМПовторение. Обратная теорема.Прямая, проведенная в плоскости через основание наклонной перпендикулярно к

наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Н-я




Слайд 6 П-я 1

А
В
Из точки М проведен перпендикуляр МВ к

П-я 1АВИз точки М проведен перпендикуляр МВ к плоскости прямоугольника АВСD.

плоскости прямоугольника АВСD. Докажите, что треугольники АМD и МСD

прямоугольные.

D

С



М







Н-я 1

Н-я 2

П-я 2



№147.

Слайд 7 П-я 1

D
А
Через вершину А прямоугольника АВСD проведена прямая

П-я 1DАЧерез вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная к

АК, перпендикулярная к плоскости прямоугольника. Известно, что КD =

6 см, КВ = 7 см, КС = 9 см. Найдите:
а) расстояние от точки К до плоскости прямоугольника АВСD; б) расстояние между прямыми АК и СD.

С

В



K







Н-я 1

Н-я 2

П-я 2



№150.

КА – искомое расстояние

?

АD – общий перпендикуляр
АD – искомое расстояние


Найдем другие прямые углы…

Слайд 8
В
Через вершину B квадрата АВСD проведена прямая ВF,

ВЧерез вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его

перпендикулярная к его плоскости. Найдите расстояния от точки F

до прямых, содержащих стороны и диагонали квадрата, если ВF = 8 дм, АВ = 4 дм.

D

С

№152.

4

1) Расстояние от точки F до прямой АВ?


2) Расстояние от точки F до прямой ВС?



3) Расстояние от точки F до прямой АD?

П-я 1



Н-я 1


Н-я 2

П-я 2




А


4) … от точки F до прямой DC?


Слайд 9
В
Через вершину B квадрата АВСD проведена прямая ВF,

ВЧерез вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его

перпендикулярная к его плоскости. Найдите расстояния от точки F

до прямых, содержащих стороны и диагонали квадрата, если ВF = 8 дм, АВ = 4 дм.

D

С

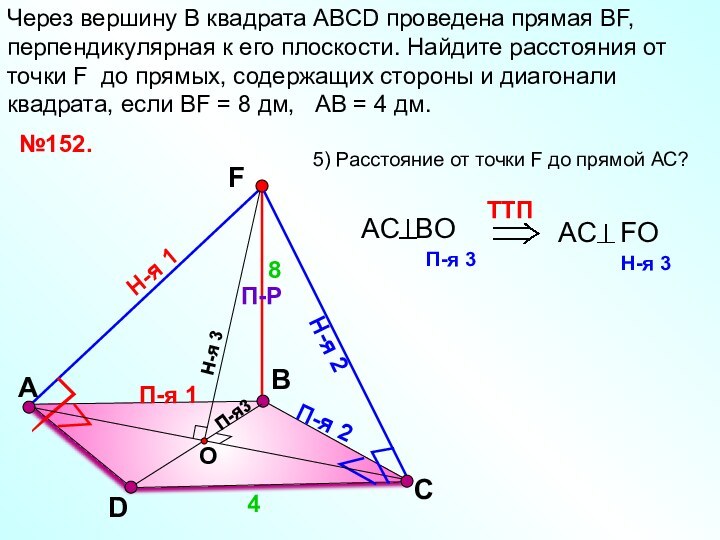
№152.

4


П-я 1



Н-я 1


Н-я 2

П-я 2







Н-я 3

П-я3

О

5) Расстояние от точки F до прямой АС?




А



Слайд 10


Прямая ОК перпендикулярна к плоскости ромба АВСD, диагонали

Прямая ОК перпендикулярна к плоскости ромба АВСD, диагонали которого пересекаются в

которого пересекаются в точке О. а) Докажите, что расстояние

от точки К до всех прямых содержащих стороны ромба, равны. б) Найдите это расстояние, если
ОК = 4,5 дм, АС = 6 дм, ВD = 8 дм.

А


К

O



D



С



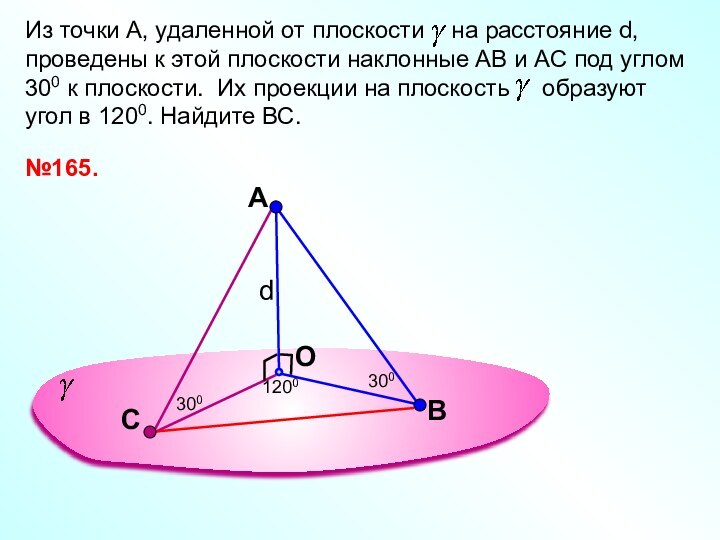
№157.

В






Слайд 11


В

М

А

D






№158.
С


600
25 см

ВМАD№158.С60025 см

Слайд 12 П-Р
Углом между прямой и плоскостью, пересекающей эту прямую

П-РУглом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной

и не перпендикулярной к ней, называется угол между прямой

и ее проекцией на плоскость.

Н-я


Слайд 13
Найти угол между наклонными и плоскостью
(описать алгоритм

Найти угол между наклонными и плоскостью (описать алгоритм построения).

построения).









Слайд 14


П-я
Прямая ВD перпендикулярна к плоскости треугольника АВС.

П-я Прямая ВD перпендикулярна к плоскости треугольника АВС. Известно, что ВD

Известно, что ВD = 9 см, АС = 10

см, ВС = ВА = 13 см. Найдите: а) расстояние от точки D до прямой АС;
б) площадь треугольника АСD.

А

С

В

№154 (дом).

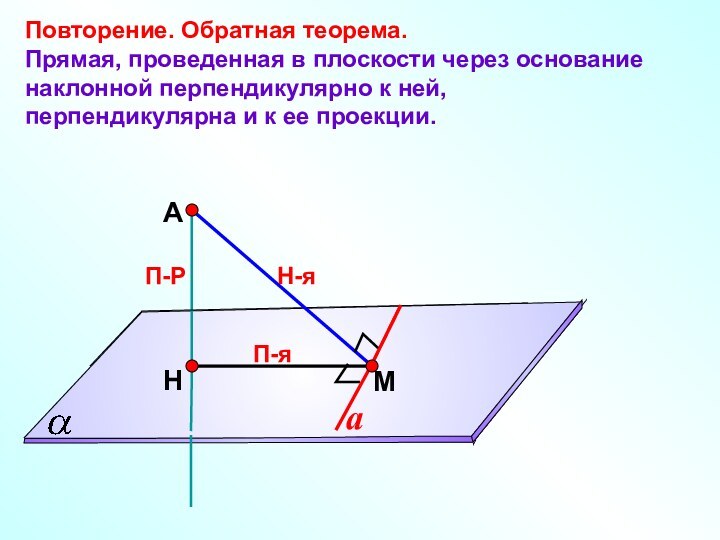
П-Р

Н-я

МD – искомое расстояние


Слайд 15 Если прямая перпендикулярна к плоскости, то ее проекцией

Если прямая перпендикулярна к плоскости, то ее проекцией на эту плоскость

на эту плоскость является точка пересечения этой прямой с

плоскостью. В таком случае угол между прямой и плоскостью считается равным 900.

Слайд 16 Если прямая параллельна плоскости, то ее проекцией на

Если прямая параллельна плоскости, то ее проекцией на плоскость является прямая,

плоскость является прямая, параллельная данной. В этом случае понятие

угла между прямой и плоскостью мы не вводим. (Иногда договариваются считать, что угол между параллельными прямой и плоскостью равен 00)

a

  • Имя файла: teorema-o-treh-perpendikulyarah-10-klass.pptx
  • Количество просмотров: 162
  • Количество скачиваний: 2
- Предыдущая Именительный падеж имён существительных
Следующая - Молдавия

Похожие презентации

Геометрические задачи на построение Геометрические задачи на построение 205
Презентация по математике на тему Луч и угол (7 класс) Презентация по математике на тему Луч и угол (7 класс) 154
Параллелепипед 5 класс Параллелепипед 5 класс 144
Презентация по геометрии на тему Параллельные прямые (7 класс) Презентация по геометрии на тему Параллельные прямые (7 класс) 153
Признаки равенства треугольников Признаки равенства треугольников 147
Некоторые свойства прямоугольного треугольника урок изучения нового материала 7 класс Некоторые свойства прямоугольного треугольника урок изучения нового материала 7 класс 166
Презентация к уроку геометрии т.Пифагора Презентация к уроку геометрии т.Пифагора 63
РОМБ РОМБ 127
Преобразования графиков функции Преобразования графиков функции 152
Презентация к уроку по геометрии Свойство биссектрисы и треугольника.Подобные треугольники 8 класс Презентация к уроку по геометрии Свойство биссектрисы и треугольника.Подобные треугольники 8 класс 180
Презентация по математике Признаки параллельности прямых Презентация по математике Признаки параллельности прямых 175
Геометрия и архитектура Геометрия и архитектура 232
Стереометрия. Задачи по готовым чертежам. Презентация Стереометрия. Задачи по готовым чертежам. Презентация 180
Тетраэдр, виды сечений и решение задач по тетраэдру Тетраэдр, виды сечений и решение задач по тетраэдру 146
Тетраэдр Параллелепипед Тетраэдр Параллелепипед 150
Измерение отрезков и углов Измерение отрезков и углов 223
Презентация по геометрии на тему Перпендикулярность прямой и плокости Презентация по геометрии на тему Перпендикулярность прямой и плокости 157
Круги Эйлера и их практическое применение Круги Эйлера и их практическое применение 166
Египетский треугольник Египетский треугольник 153
Презентация по геометрии на тему Геометрия в строительстве. Ученицы 9 класса. Презентация по геометрии на тему Геометрия в строительстве. Ученицы 9 класса. 240
Презентация к уроку геометрии Нахождение площадей нестандартных фигур 9 класс Презентация к уроку геометрии Нахождение площадей нестандартных фигур 9 класс 183
Презентация по теме Теорема об отношении площадей треугольников, имеющих по равному углу. Презентация по теме Теорема об отношении площадей треугольников, имеющих по равному углу. 196
Расстояние от точки до плоскости в пространстве Расстояние от точки до плоскости в пространстве 185
Презентация к уроку геометрии в 7 классе Конкурс веселых математиков Презентация к уроку геометрии в 7 классе Конкурс веселых математиков 157
Площади фигур геометрия Площади фигур геометрия 179
Теорема о трех перпендикулярах геометрия 10 класс Теорема о трех перпендикулярах геометрия 10 класс 183
Презентация по геометрии на тему Второй признак равенства треугольников (7 класс) Презентация по геометрии на тему Второй признак равенства треугольников (7 класс) 138
Презентация по математике на тему Фигуралардың теңдігі(7 класс) Презентация по математике на тему Фигуралардың теңдігі(7 класс) 254
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник 174
Определение и признак перпендикулярности плоскостей Определение и признак перпендикулярности плоскостей 191