- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Водородоподобные атомы
Содержание
- 2. Гипотеза о том, что вещества состоят из
- 3. МОДЕЛИ АТОМАРанние модели:1) Модель Томсона – “булочка
- 4. Опыт Резерфорда по рассеянию α-частицЭрнст Резерфорд
- 5. Альфа-частица образована 2-мя протонами и 2-мя нейтронами,
- 6. Резерфорд направил поток α-частиц на золотую фольгу
- 7. Резерфорд сделал вывод: Причиной рассеяния α-частицы является
- 8. Планетарная модель атома РезерфордаАтом представляет собой подобие
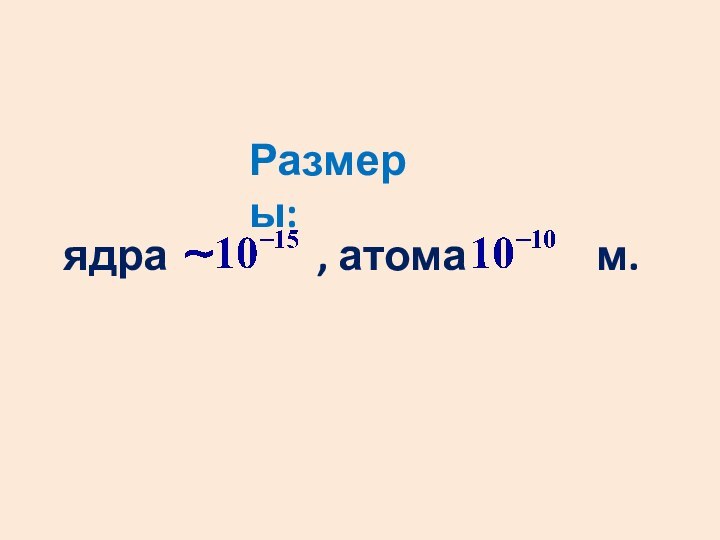
- 9. ядра
- 10. Неустойчивость атома РезерфордаСогласно классической электродинамике электрон при
- 11. Теория водородоподобного атома по БоруПри построении теории
- 12. Водородоподобный атом – это атом с одним
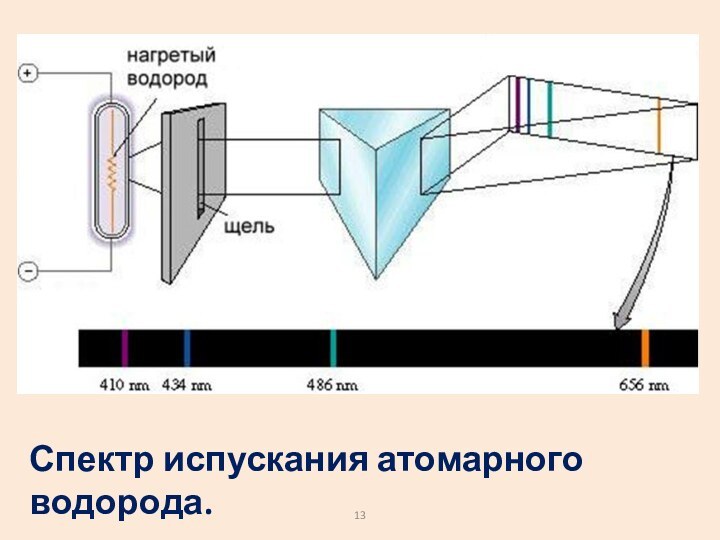
- 13. Спектр испускания атомарного водорода.
- 14. Спектр атома водорода образован сериями линий. Линии
- 15. Бальмер подобрал формулу для частот спектральных линий:
- 16. Постулаты БораАтом может находится только в особых
- 17. Второй постулат Бора (правило частот)При переходе атома
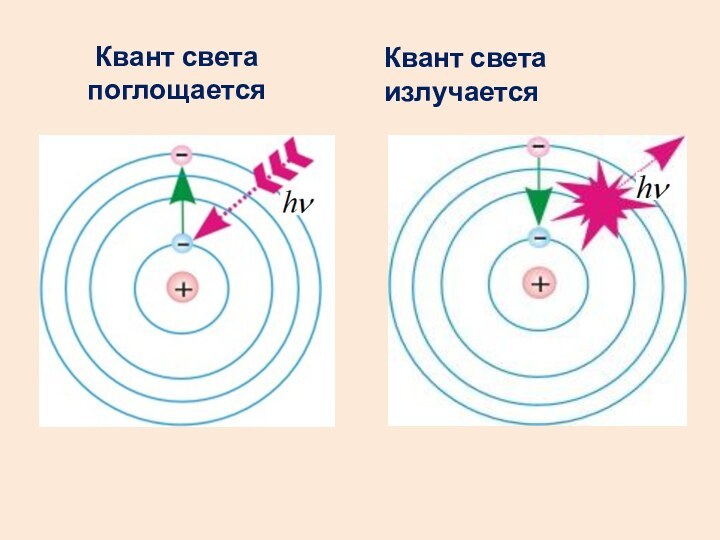
- 18. Квант света поглощаетсяКвант света излучается
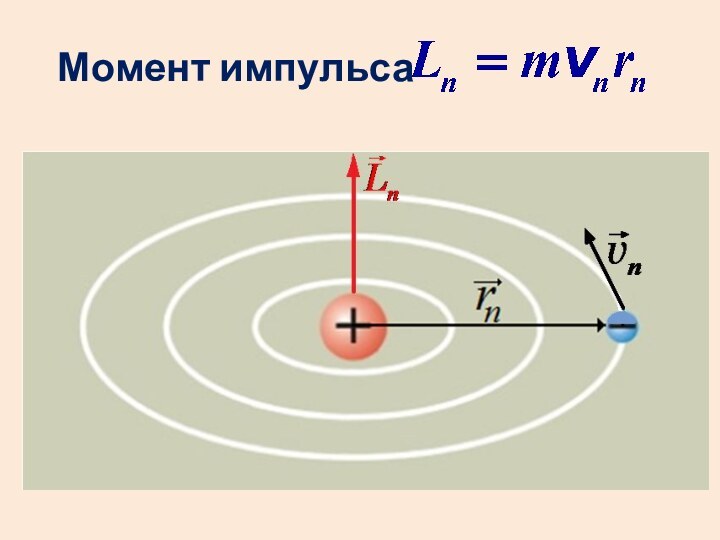
- 19. Третий постулат (квантование орбит)Момент импульса электрона в
- 20. Момент импульса
- 21. На электрон действует кулоновская сила. По 2-му закону Ньютона
- 22. Радиус ближайшей к ядру орбиты называют первым боровским радиусом.заряд ядра,
- 23. Полная энергия электрона в атоме:Энергия электрона на первой боровской орбите в атоме водорода:
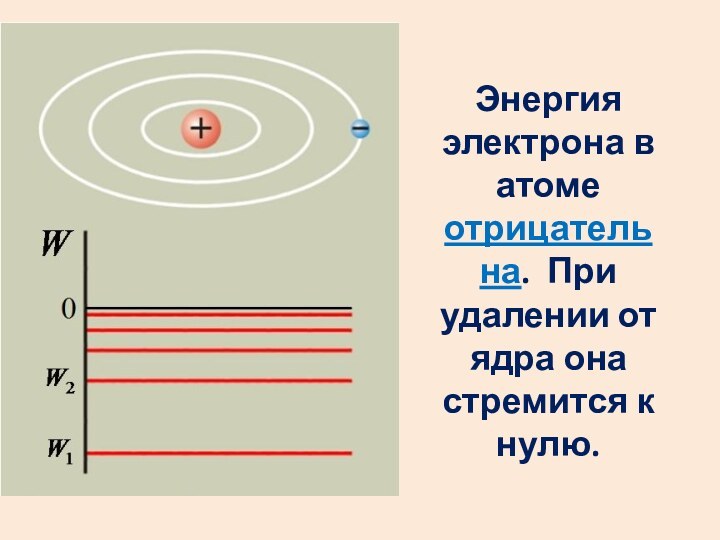
- 24. Энергия электрона в атоме отрицательна. При удалении от ядра она стремится к нулю.
- 25. Частота излучения при переходе с n-го на
- 26. Спектры излучения водорода
- 27. Спектры поглощения водорода
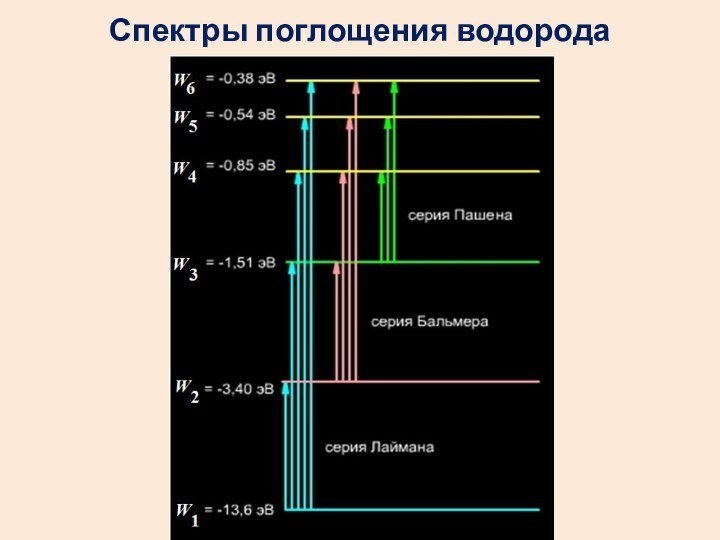
- 28. Для серииЛаймана m=1, n=2, 3, 4,….Бальмера m=2, n=3, 4, 5….Пашена m=3, n=4, 5, 6,….
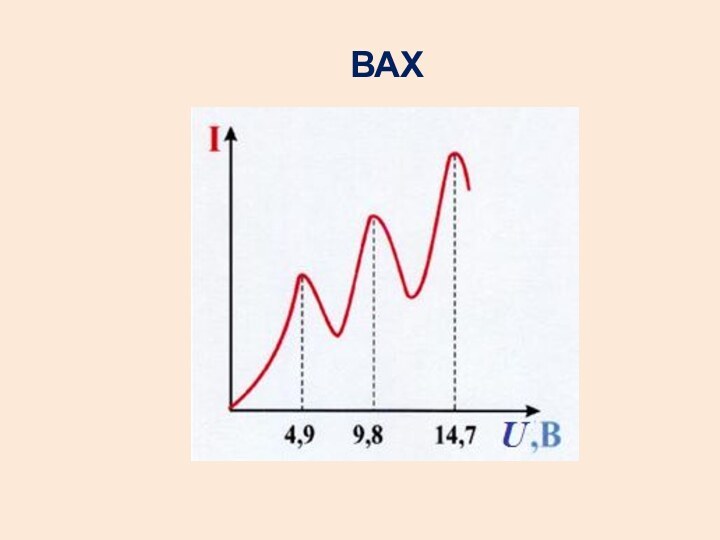
- 29. Опыт Франка и ГерцаКвантовые постулаты Бора нашли
- 30. Электроны, испускаемые катодом К, ускоряются в электрическом
- 31. ВАХ
- 33. Теория Бора дала не только качественное, но
- 34. Достоинства и недостатки теории БораДостоинства: 1. Объяснила
- 35. Квантовая теория атома
- 36. Электрон в атоме находится в потенциальной яме.
- 37. n=1, 2,… - главное квантовое число.Оно
- 38. Квантование момента импульса l = 0, 1,
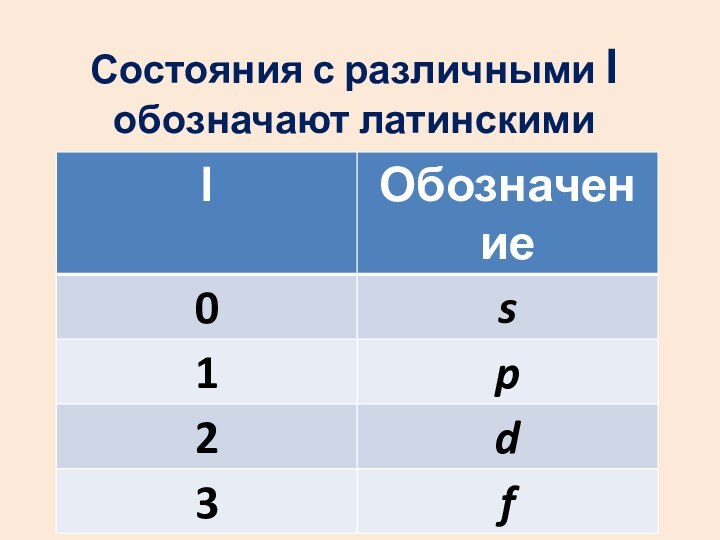
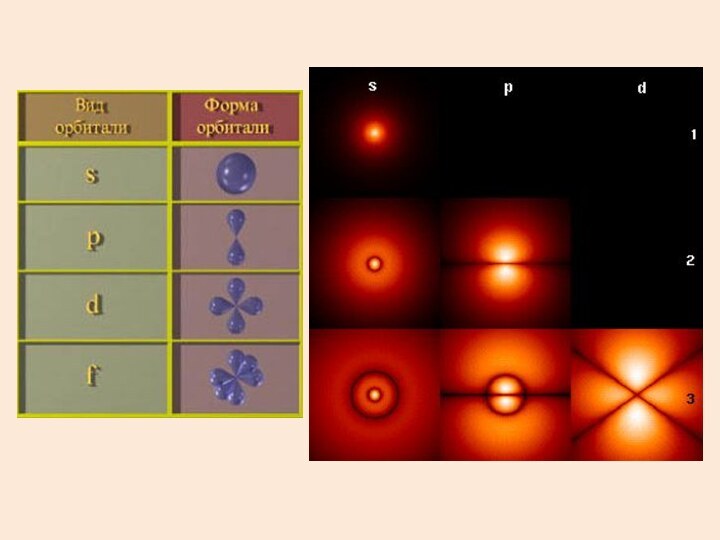
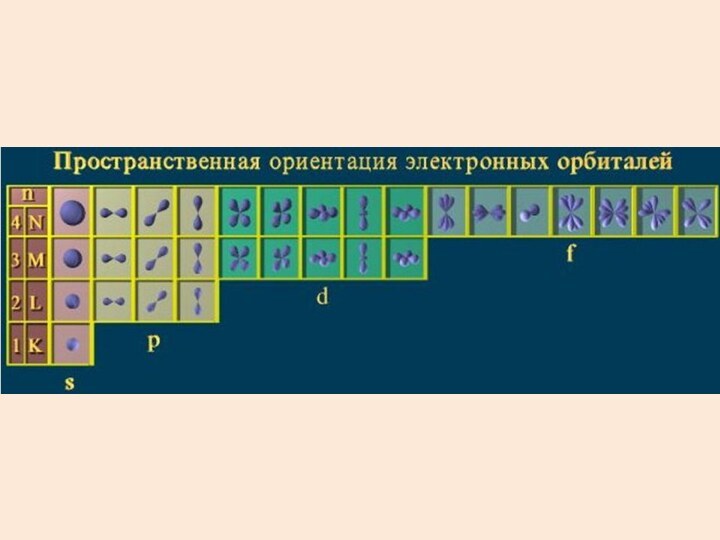
- 39. Состояния с различными l обозначают латинскими буквами
- 41. Выделим в пространстве какое-либо направление, например, направление
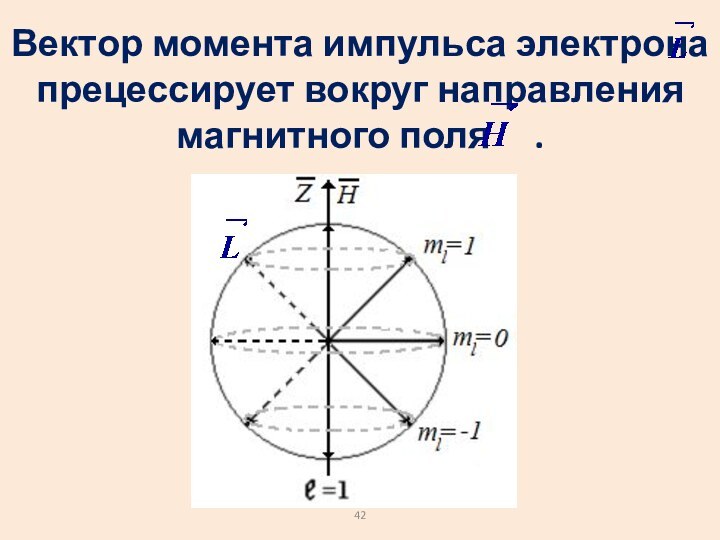
- 42. Вектор момента импульса электрона прецессирует вокруг направления магнитного поля .
- 43. Проекция момента импульса на направ-ление z имеет
- 45. Аналогично механическому моменту импульса квантуется орбитальный магнитный момент электрона:
- 46. Квантование спина Спин электрона
- 47. Собственный магнитный момент электрона:
- 48. Проекция спина электрона на направление магнитного поля
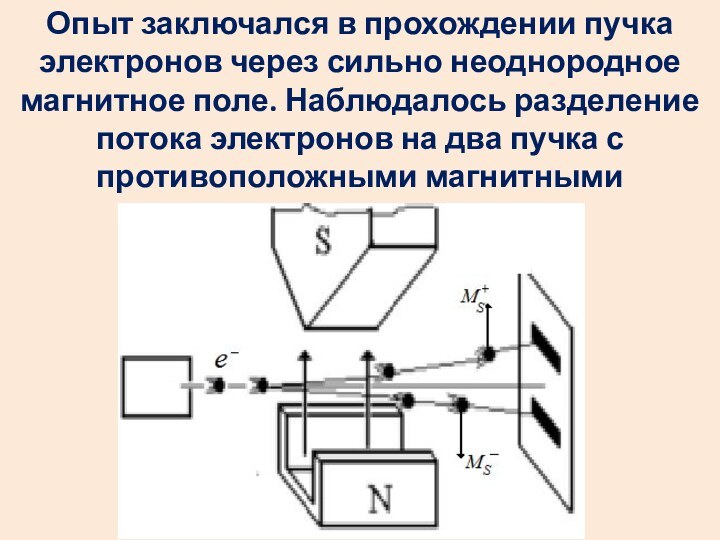
- 49. Квантование спина электрона экспериментально доказано опытами Штерна и Герлаха.
- 50. Опыт заключался в прохождении пучка электронов через
- 51. Вывод:Состояние электрона в атоме определяется набором 4-х
- 52. Число состояний на энергетичес-ком уровне с главным квантовым числом n:с учетом спина
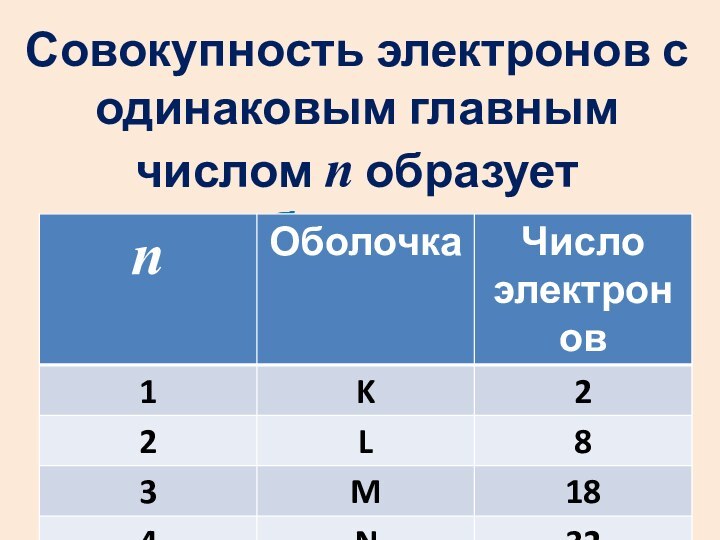
- 53. Совокупность электронов с одинаковым главным числом n образует оболочку.
- 54. Правила отбора: возможны лишь такие переходы между состояниями, при которых
- 55. Скачать презентацию
- 56. Похожие презентации
Гипотеза о том, что вещества состоят из атомов, впервые была высказана Левкиппом и Демокритом примерно в IV веке до н. э.





































Слайд 3
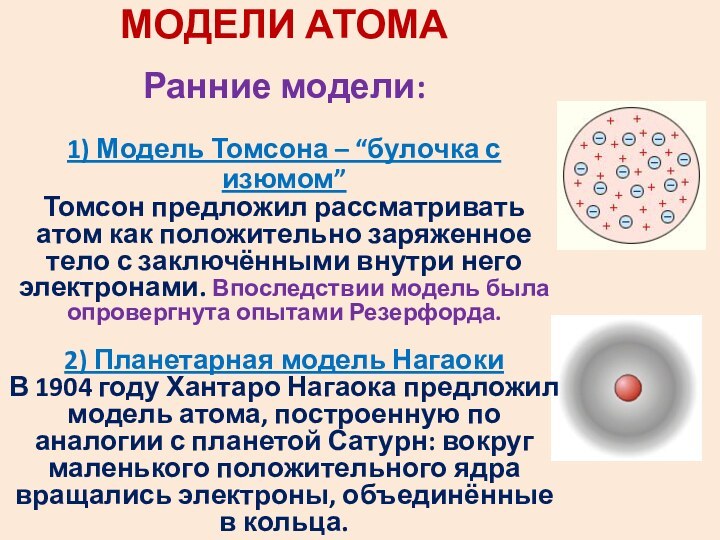
МОДЕЛИ АТОМА
Ранние модели:
1) Модель Томсона – “булочка с
изюмом”
Томсон предложил рассматривать атом как положительно заряженное тело
с заключёнными внутри него электронами. Впоследствии модель была опровергнута опытами Резерфорда. 2) Планетарная модель Нагаоки
В 1904 году Хантаро Нагаока предложил модель атома, построенную по аналогии с планетой Сатурн: вокруг маленького положительного ядра вращались электроны, объединённые в кольца.
Модель оказалось ошибочной, но послужила основой модели атома Резерфорда.
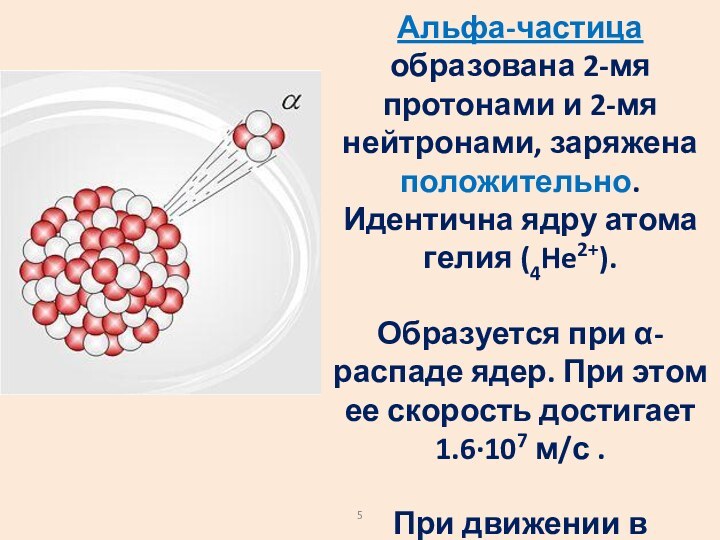
Слайд 5 Альфа-частица образована 2-мя протонами и 2-мя нейтронами, заряжена
положительно. Идентична ядру атома гелия (4He2+).
Образуется при α-распаде
ядер. При этом ее скорость достигает 1.6∙107 м/с . При движении в веществе α-частица создаёт сильную ионизацию и в результате быстро теряет энергию.
Слайд 6 Резерфорд направил поток α-частиц на золотую фольгу толщиной
около 0,1 мкм. Большинство частиц пролетели сквозь фольгу, но
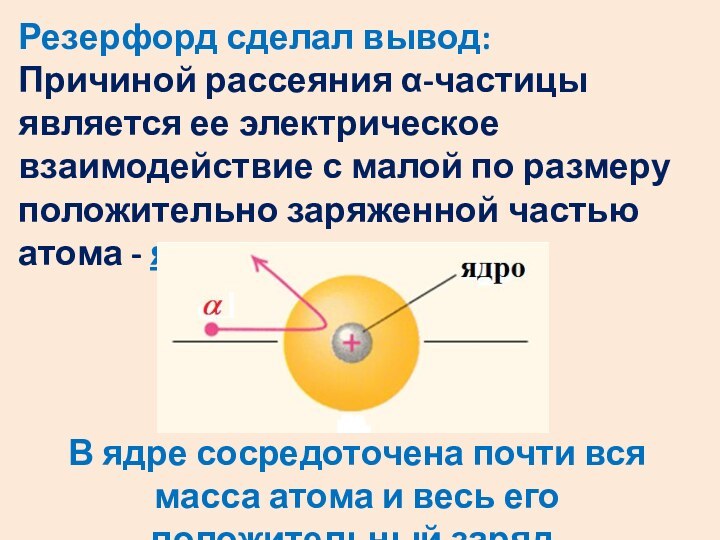
некоторые отклонились на очень большие углы вплоть до 180 град.Слайд 7 Резерфорд сделал вывод: Причиной рассеяния α-частицы является ее электрическое
взаимодействие с малой по размеру положительно заряженной частью атома
- ядром.В ядре сосредоточена почти вся масса атома и весь его положительный заряд.
Слайд 8
Планетарная модель атома Резерфорда
Атом представляет собой подобие планетной
системы, в которой электроны движутся по орбитам вокруг тяжёлого
положительно заряженного ядра..
Слайд 10
Неустойчивость атома Резерфорда
Согласно классической электродинамике электрон при движении
с центростреми-тельным ускорением должен излучать электромагнитные волны и терять
энергию. В итоге он упадёт на ядро.Для объяснения стабильности атомов Нильсу Бору пришлось ввести особые предположения – постулаты. Постулаты Бора показали, что для атома классическая механика неприменима.
Слайд 11
Теория водородоподобного атома по Бору
При построении теории Бор
опирался на опыт Резерфорда и данные по спектрам атомарных
газов. Согласно опыту эти спектры линейчатые.
Слайд 12
Водородоподобный атом – это атом с одним внешним
электроном: Na, K, Rb, Cs.
Спектр атома – это
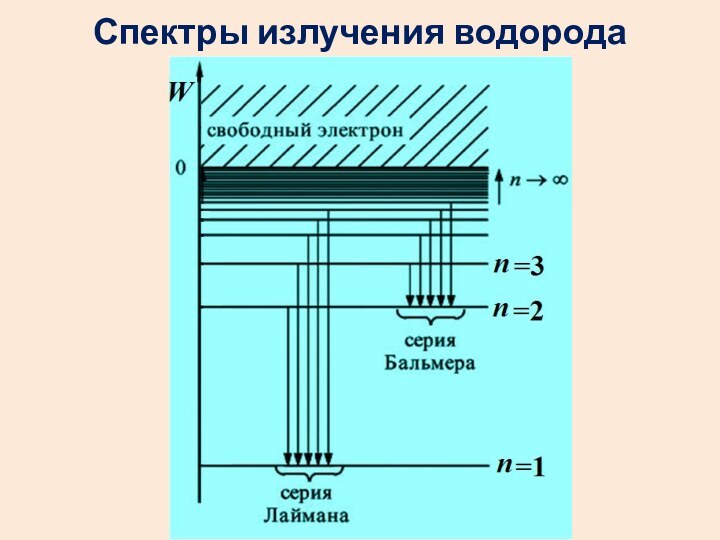
набор излучаемых или поглощаемых частот.Слайд 14 Спектр атома водорода образован сериями линий. Линии сгущаются
к высокочастотной границе серии.
В видимой области наблюдается
серия
Бальмера. Еще одна серия есть в УФ области. А в ИК диапазоне – много серий.
ИК
УФ
видимый свет
Серии: … Брэкета Пашена Бальмера Лаймана
Слайд 15
Бальмер подобрал формулу для частот спектральных линий:
Для
серии Бальмера m = 2, n = 3, 4, 5, ... .
Для серии Лаймана m = 1,
n = 2, 3, 4, ... . R - постоянная Ридберга
R = 3,3·1015 Гц.
Слайд 16
Постулаты Бора
Атом может находится только в особых стационарных
или квантовых состояниях, каждому из которых соответствует определенная энергия
Wn.В стационарных состояниях атом
не излучает.
Первый постулат Бора (постулат стационарных состояний)
Слайд 17
Второй постулат Бора (правило частот)
При переходе атома из
одного стационарного состояния с энергией Wn в другое с
энергией Wm излучается или поглощается квант, энергия которого равна разности энергий этих состояний.
Слайд 19
Третий постулат (квантование орбит)
Момент импульса электрона в атоме
принимает только дискретные значения, кратные постоянной Планка:
m
– масса электрона,vn – его скорость на орбите радиуса rn , n = 1, 2, 3 …
Слайд 23
Полная энергия электрона в атоме:
Энергия электрона на первой
боровской орбите в атоме водорода:
Слайд 25
Частота излучения при переходе с n-го
на m-й
уровень энергии:
R=3,3∙1015 Гц - частотная константа Ридберга, ее значение
совпало с угаданным БальмеромДлина волны :
R’=1,1∙107 м-1 - волновая константа Ридберга
Слайд 29
Опыт Франка и Герца
Квантовые постулаты Бора нашли экспериментальное
подтверждение в опыте Дж.Франка и Г. Герца.
Опыт заключался
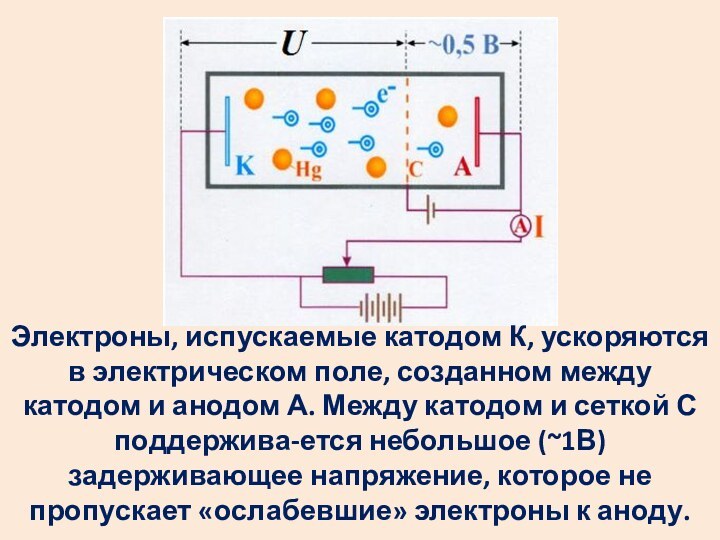
в пропускании электронного пучка через пары ртути. Слайд 30 Электроны, испускаемые катодом К, ускоряются в электрическом поле,
созданном между катодом и анодом А. Между катодом и
сеткой С поддержива-ется небольшое (~1В) задерживающее напряжение, которое не пропускает «ослабевшие» электроны к аноду.Слайд 33 Теория Бора дала не только качественное, но и
количественное описание атомных спектров, а также опытов Франка и
Герца.
Слайд 34
Достоинства и недостатки теории Бора
Достоинства:
1. Объяснила линейчатый
спектр атомов.
2. Предсказала значения частот.
3. Правильно определила размеры атома
водорода.4. Рассчитала константу Ридберга.
Недостатки:
1. Для объяснения квантовых явлений использовала не только квантовую, но и классическую физику.
2. Не смогла рассчитать интенсивность спектра излучения.
3. Не дает объяснений причин перехода между уровнями энергии
4. Не верна для многоэлектронных атомов (Не и т.п.)
Слайд 36 Электрон в атоме находится в потенциальной яме. Применим
к нему уравнение Шредингера
Решение уравнения дает дискретные значения энергии
совпадающие
с полученными Бором.
Слайд 37
n=1, 2,… - главное квантовое число.
Оно определяет
энергию электрона, степень его удаленности от ядра, размеры электронной
орбиты.
Слайд 38
Квантование момента импульса
l = 0, 1,
2, …, n-1 - орбитальное квантовое число.
Модуль момента импульса
электрона L принимает дискретные значения:Оно определяет размер и форму электронной орбиты.
Слайд 41 Выделим в пространстве какое-либо направление, например, направление магнитного
поля.
Проекция момента импульса электрона на это направление может
иметь только дискретные значения.Слайд 43 Проекция момента импульса на направ-ление z имеет дискретные
значения:
m – магнитное квантовое число
Оно задает ориентацию
орбиты в пространстве.Слайд 45 Аналогично механическому моменту импульса квантуется орбитальный магнитный момент
электрона:
Слайд 46
Квантование спина
Спин электрона –
это его собственный момент импульса.
Спин квантуется по закону:
спиновое
квантовое числоСлайд 48 Проекция спина электрона на направление магнитного поля может
принимать только одно из двух значений
магнитное спиновое квантовое число
Слайд 50 Опыт заключался в прохождении пучка электронов через сильно
неоднородное магнитное поле. Наблюдалось разделение потока электронов на два
пучка с противоположными магнитными моментами МS+ и МS-- .
Слайд 51
Вывод:
Состояние электрона в атоме определяется набором 4-х квантовых
чисел:
главного n, (n = 1, 2, 3,
…)орбитального l, (l = 0, 1, 2, … , n-1)
магнитного m, (m = - l, …-1, 0, 1, …, l)
спинового магнитного mS , (mS = -1/2, +1/2)