Презентация на тему Задачи на смеси и сплавы (7 класс)

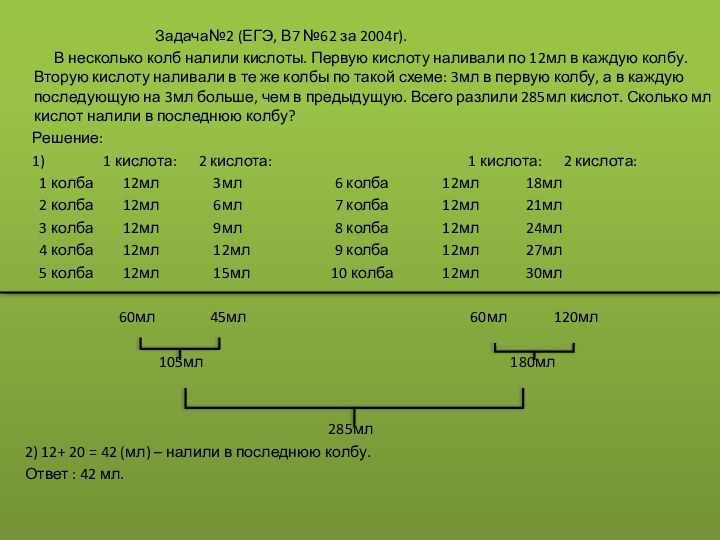
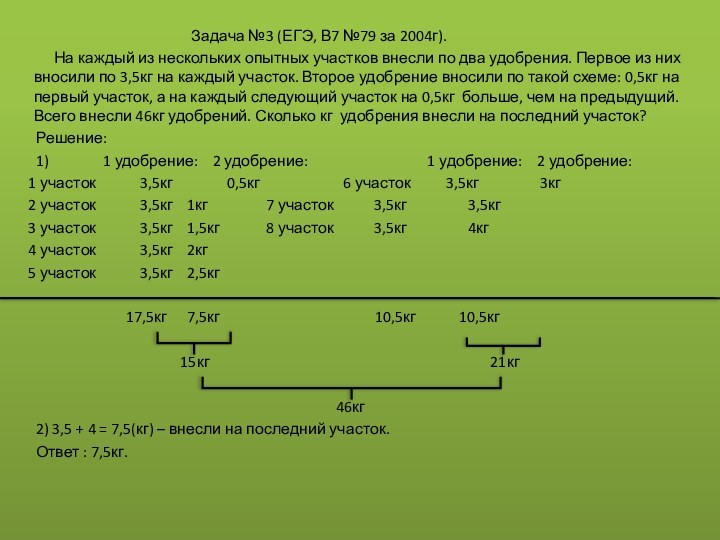
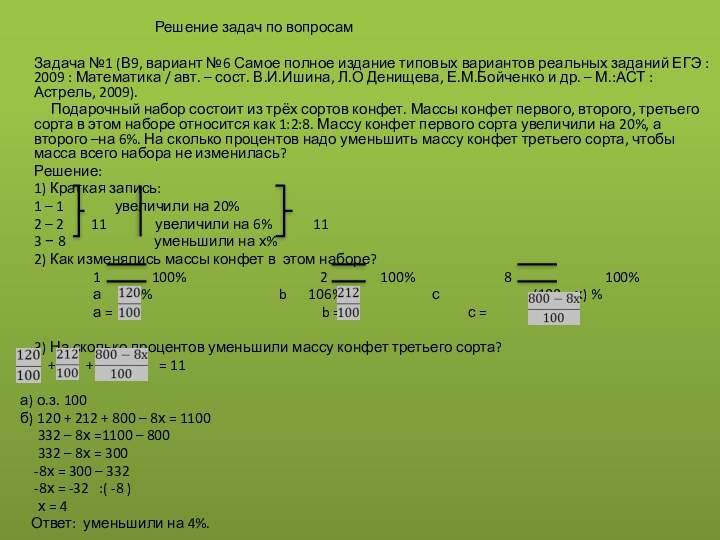
Историческая справка

Многие сплавы, которые содержат совсем незначительные добавки дорогих и редких металлов, приобретают значительную устойчивость к коррозии и прекрасные механические свойства. Например, добавки родия и иридия к платине так сильно повышают её твёрдость, что изделия из неё – лабораторная посуда, детали машин для получения стекловолокна – становится практически вечными. Другие сплавы настолько непохожи на металлы, из которых состоят, что люди долгое время считали их не смесями, а индивидуальными веществами. И лишь много позже сумели объяснить их состав и способ получения. Поэтому из металлов делают сплавы. В технике чаще всего используется именно сплавы, а не чистые металлы.
Наиболее продуктивной и интересной формой знакомства с биографическими и научными достижениями ученых является поиск информации и решения задач, составленных на основе исторического материала, фрагментов из сочинений ученых, биографического материала.

Решение задач на “растворы, смеси и

сплавы” являются хорошим накоплением опыта решения таких задач. В таких задачах прослеживается системный подход к ним и происходит успешная отработка и закрепление интеллектуальных умений, которые помогут нам решать задачи по физике и химии.
Данная работа относится к проблемно-исследовательскому разделу.







Цель работы научиться решать задачи на смеси и сплавы.

При решении задач на смеси и сплавы я использовала теоретические сведения о процентах, пропорциях и уравнениях.


Уравнением называют равенство, содержащее букву, значение которой надо найти.

Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения.

Решить уравнение значит найти все его корни (или убедиться, что это уравнение не имеет ни одного корня).

Пропорция

Пропорция – равенство двух отношений.

Основное свойство пропорции : произведение крайних членов пропорции равно произведению средних членов пропорции : ad=bc

задач на пропорцию
Задача №1 (ЕГЭ вариант №349

за 2003г.)
Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из -за дождей влажность смеси повысилась на 2%. Найдите массу привезённой смеси, если со клада было отправлено 400 кг.
Решение:
1) 100% - 18% =82% -концентрация сухого вещества
2) 400 кг 100%
х кг 82%

х = 40082:100 = 328(кг) – масса сухого вещества.
3) 18% + 2% = 20% - концентрация влаги.
4) 328 кг 80%
у кг 100%

у = 328100:80=410(кг)
Ответ: 410 кг.

Задача №2 : № 3 (ЕГЭ:

Математика: Контрол. измерит. материалы / Под ред. Ковалевой Г.С.. – М.: Просвещение, 2003):
Собрали 140 кг грибов, влажность которых составляла 98%. После подсушивания их влажность снизилась до 93%. Какова стала масса грибов после подсушивания?
Решение:
100% - 98% = 2% - концентрация сухого вещества
140 кг 100 %
х кг 2%

х = = (кг) – масса сухого вещества
100% - 93% = 7% - стала концентрация сухого вещества
кг 7 %
у кг 100%

у = = = 40 (кг) – масса сухих грибов

Ответ: 40 кг. 
 

Гипотеза
Можно ли задачи на смеси и сплавы решать другими способами.
 
 

Решение задач методом подбора:
Задача №1(ЕГЭ, В7 №76 за 1004г).
На каждый из нескольких опытных участков внесли по два удобрения. Первое из них вносили по 1кг на каждый участок. Второе удобрение вносили по следующей схеме: 200г на первый участок, а на каждый следующий участок на 200г больше, чем на предыдущий. Всего внесли 18кг удобрений. Сколько кг первого удобрения внесли на все участки?
Решение:
1) 1 удобрение: 2 удобрение: 1 удобрение: 2 удобрение:
1 участок 1кг 200г 6 участок 1кг 1200г
2 участок 1кг 400г 7 участок 1кг 1400г
3 участок 1кг 600г 8 участок 1кг 1600г
4 участок 1кг 800г 9 участок 1кг 1800г
5 участок 1кг 1000г

5кг 3кг 4кг 6кг

8кг 10кг


18кг
Ответ : 9кг первого удобрения внесли на все участки.

Задача№2 (ЕГЭ, В7 №62 за 2004г).
В несколько колб налили кислоты. Первую кислоту наливали по 12мл в каждую колбу. Вторую кислоту наливали в те же колбы по такой схеме: 3мл в первую колбу, а в каждую последующую на 3мл больше, чем в предыдущую. Всего разлили 285мл кислот. Сколько мл кислот налили в последнюю колбу?
Решение:
1) 1 кислота: 2 кислота: 1 кислота: 2 кислота:
1 колба 12мл 3мл 6 колба 12мл 18мл
2 колба 12мл 6мл 7 колба 12мл 21мл
3 колба 12мл 9мл 8 колба 12мл 24мл
4 колба 12мл 12мл 9 колба 12мл 27мл
5 колба 12мл 15мл 10 колба 12мл 30мл

60мл 45мл 60мл 120мл

105мл 180мл
 

285мл
2) 12+ 20 = 42 (мл) – налили в последнюю колбу.
Ответ : 42 мл.

Задача №3 (ЕГЭ, В7 №79 за 2004г).
На каждый из нескольких опытных участков внесли по два удобрения. Первое из них вносили по 3,5кг на каждый участок. Второе удобрение вносили по такой схеме: 0,5кг на первый участок, а на каждый следующий участок на 0,5кг больше, чем на предыдущий. Всего внесли 46кг удобрений. Сколько кг удобрения внесли на последний участок?
Решение:
1) 1 удобрение: 2 удобрение: 1 удобрение: 2 удобрение:
1 участок 3,5кг 0,5кг 6 участок 3,5кг 3кг
2 участок 3,5кг 1кг 7 участок 3,5кг 3,5кг
3 участок 3,5кг 1,5кг 8 участок 3,5кг 4кг
4 участок 3,5кг 2кг
5 участок 3,5кг 2,5кг

17,5кг 7,5кг 10,5кг 10,5кг

15кг 21кг

46кг
2) 3,5 + 4 = 7,5(кг) – внесли на последний участок.
Ответ : 7,5кг.

Решение задач на кратное сравнение

Задача №1 (7.29 (1) Алгебра: сб.заданий для подготовки к итоговой аттестации в 9кл./[Л.В.Кузнецова, С.Б.Суворова, Е.А.Бунимович и др.]. – М. : Просвещение, 2006.)
Влажность свежескошенной травы 60%, сена20%. Сколько сена получится из 1т свежескошенной травы?
Решение:
1) 100% - 60% = 40% −составляет сухое вещество.
2) 100% - 20% = 80% −стало составлять сухое вещество.
3) 80% : 40% = 2(р) –во столько раз сухое вещество увеличилось в сене.
4) 1000кг : 2 = 500(кг)
Ответ : 500кг сена.

Алгебра: сб.заданий для подготовки к итоговой аттестации в 9кл./[Л.В.Кузнецова,

С.Б.Суворова, Е.А.Бунимович и др.]. – М. : Просвещение, 2006.)
В свежих яблоках 80% воды, а в сушённых −20%. На сколько процентов уменьшится масса яблок при сушке?
Решение:
1) 100% - 80% = 20% −составляет сухое вещество.
2) 100% - 20% = 80% − стало составлять сухое вещество.
3) 80% : 20% = 4(р) –масса сухого вещества увеличилась в 4 раза, тогда масса яблок уменьшится в 4 раза.
4) 100% : 4 = 25% −составляли яблоки после сушки.
5) 100% - 25% = 75%
Ответ: на 75%.
 
 

Решение задач по вопросам

Задача №1 (В9, вариант №6 Самое полное издание типовых вариантов реальных заданий ЕГЭ : 2009 : Математика / авт. – сост. В.И.Ишина, Л.О Денищева, Е.М.Бойченко и др. – М.:АСТ : Астрель, 2009).
Подарочный набор состоит из трёх сортов конфет. Массы конфет первого, второго, третьего сорта в этом наборе относится как 1:2:8. Массу конфет первого сорта увеличили на 20%, а второго –на 6%. На сколько процентов надо уменьшить массу конфет третьего сорта, чтобы масса всего набора не изменилась?
Решение:
1) Краткая запись:
1 – 1 увеличили на 20%
2 – 2 11 увеличили на 6% 11
3 − 8 уменьшили на х%
2) Как изменялись массы конфет в этом наборе?
1 100% 2 100% 8 100%
а 120% b 106% с (100 – х) %
а = b = с =

3) На сколько процентов уменьшили массу конфет третьего сорта?
+ + = 11

а) о.з. 100
б) 120 + 212 + 800 – 8х = 1100
332 – 8х =1100 – 800
332 – 8х = 300
-8х = 300 – 332
-8х = -32 :( -8 )
х = 4
Ответ: уменьшили на 4%.

вариант №5 Самое полное издание типовых вариантов реальных заданий

ЕГЭ : 2009 : Математика / авт. – сост. В.И.Ишина, Л.О Денищева, Е.М.Бойченко и др. – М.:АСТ : Астрель, 2009).
Набор химических реактивов состоит из трёх веществ. Массы первого, второго и третьего веществ в этом наборе относятся 3: 7: 10. Массу первого вещества увеличили на 8%, а второго− на 4%. На сколько процентов надо уменьшить массу третьего вещества, чтобы масса всего набора не изменилась?
Решение:
1) Краткая запись:
1 – 3 увеличили на 8%
2 – 7 20 увеличили на 4% 20
3 – 10 уменьшили на х%
2) Как изменялись массы веществ в этом наборе?
3 100% 7 100% 10 100%
а 108% b 104% с (100 – х ) %
а = b = с =

3) На сколько процентов уменьшили массу третьего вещества?
+ + = 20

а) о.з. 100
б) 324 + 728 + 1000 – 10х = 2000
324 + 728 – 10х = 1000
1052 – 10х = 1000
-10х = 1000 – 1052
-10х = -52 : (- 10)
х = 5,2
Ответ : на 5,2% уменьшили массу третьего вещества.