Презентация на тему Общие сведения о системах счисления.

Содержание

2. Система счисления — совокупность правил записи чисел с помощью определенного набора символов.
3. зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные
4. В компьютере наиболее подходящей и надежной оказалась
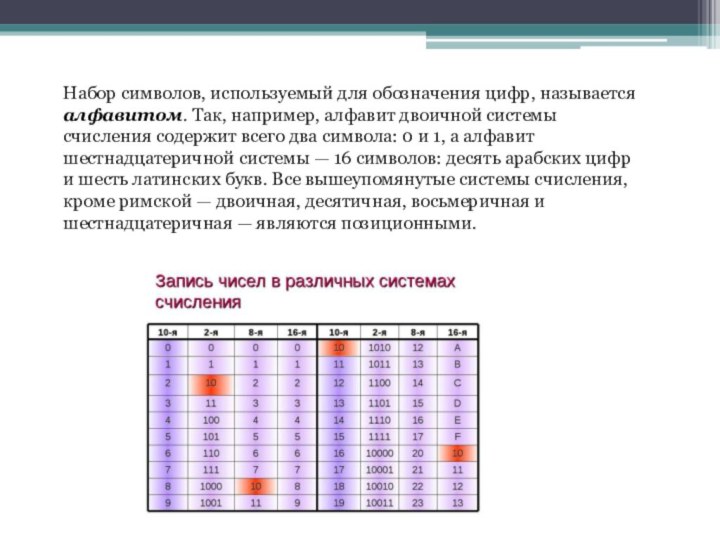
5. Набор символов, используемый для обозначения цифр, называется
6. В общем случае любое число N в
7. отрицательные значения индексов — для дробной части
8. Двоичная система счисления обладает такими же свойствами,
9. Для сравнения рассмотрим представление чисел в разных
10. Скачать презентацию
11. Похожие презентации

Система счисления — совокупность правил записи чисел с помощью определенного набора символов.

Главная
Информатика
Презентация Общие сведения о системах счисления.

Система счисления — совокупность правил записи чисел с помощью определенного набора символов.

зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные

В компьютере наиболее подходящей и надежной оказалась двоичная система счисления (р =

Набор символов, используемый для обозначения цифр, называется алфавитом. Так, например, алфавит двоичной

В общем случае любое число N в позиционной системе счисления можно представить

отрицательные значения индексов — для дробной части числа. С учетом этих обозначений

Двоичная система счисления обладает такими же свойствами, что и десятичная, только для

Для сравнения рассмотрим представление чисел в разных системах счисления как сумму слагаемых,

Презентация Общие сведения о системах счисления.

Слайды презентации

Слайд 2 Система счисления — совокупность правил записи чисел

с помощью определенного набора символов.

Слайд 3 зависимости от способа изображения чисел системы счисления делятся

на позиционные и непозиционные

Слайд 4 В компьютере наиболее подходящей и надежной оказалась двоичная

система счисления (р = 2), в которой для представления

чисел используются цифры 0 и 1. Кроме этого оказалось удобным использовать представление информации с помощью еще двух систем счисления: ♦ восьмеричной (р = 8, используемые цифры — 0, 1, 2, ..., 7); ♦ шестнадцатеричной (р = 16, используемые символы-цифры — 0, 1, 2... 9 и буквы — А, В, С, D, Е, F, заменяющие числа 10, 11, 12, 13, 14, 15 соответственно).

Слайд 5 Набор символов, используемый для обозначения цифр, называется алфавитом.

Набор символов, используемый для обозначения цифр, называется алфавитом. Так, например, алфавит

Так, например, алфавит двоичной системы счисления содержит всего два

символа: 0 и 1, а алфавит шестнадцатеричной системы — 16 символов: десять арабских цифр и шесть латинских букв. Все вышеупомянутые системы счисления, кроме римской — двоичная, десятичная, восьмеричная и шестнадцатеричная — являются позиционными.

Слайд 6 В общем случае любое число N в позиционной

В общем случае любое число N в позиционной системе счисления можно

системе счисления можно представить в следующем виде:
Np =

ak*pk + ak-1*pk-1 +...+ а1*р1 + a0*p0 + a-1*p-1 +...+ a-n*p-n
где p — основание системы счисления; k+1 — количество разрядов в целой части числа; n — количество разрядов в дробной части числа. Нижние индексы определяют местоположение цифры в числе (разряд):

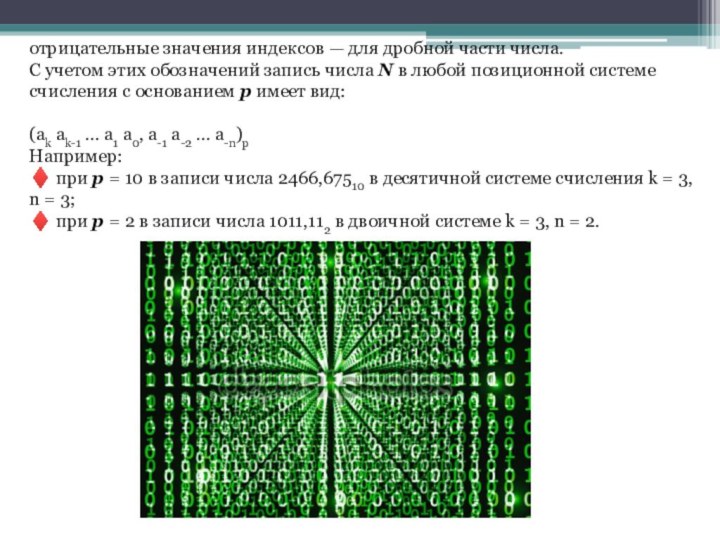
Слайд 7 отрицательные значения индексов — для дробной части числа.

отрицательные значения индексов — для дробной части числа. С учетом этих

С учетом этих обозначений запись числа N в любой

позиционной системе счисления с основанием р имеет вид: (ak ak-1 ... а1 a0, a-1 a-2 ... a-n)p
Например: ♦ при p = 10 в записи числа 2466,67510 в десятичной системе счисления k = 3, n = 3; ♦ при р = 2 в записи числа 1011,112 в двоичной системе k = 3, n = 2.

Слайд 8 Двоичная система счисления обладает такими же свойствами, что

Двоичная система счисления обладает такими же свойствами, что и десятичная, только

и десятичная, только для представления чисел используется не 10

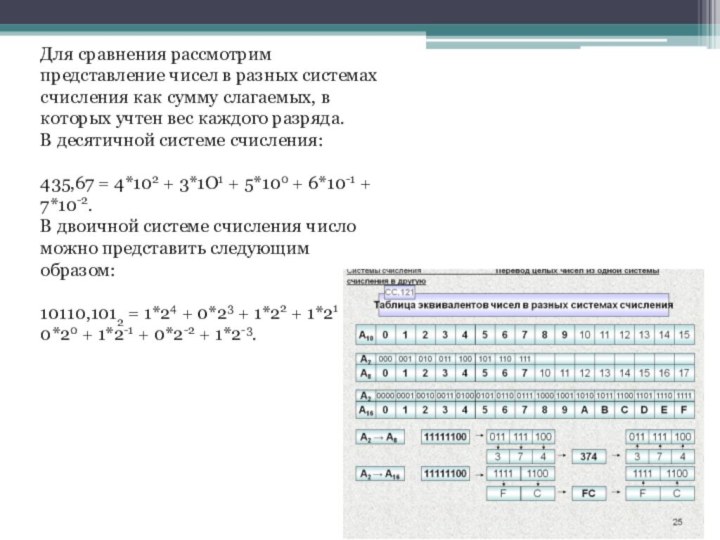
цифр, а всего две. Соответственно и разряд числа называют не десятичным, а двоичным. Основные правила выполнения арифметических действий соблюдаются точно так же, как и в десятичной системе счисления.

Слайд 9 Для сравнения рассмотрим представление чисел в разных системах

Для сравнения рассмотрим представление чисел в разных системах счисления как сумму

счисления как сумму слагаемых, в которых учтен вес каждого

разряда.
В десятичной системе счисления: 435,67 = 4*102 + 3*1О1 + 5*100 + 6*10-1 + 7*10-2.
В двоичной системе счисления число можно представить следующим образом: 10110,1012 = 1*24 + 0*23 + 1*22 + 1*21 + 0*20 + 1*2-1 + 0*2-2 + 1*2-3.