- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Системы счисления (9 класс)
Содержание
- 2. Система счисления – это знаковая система, в
- 3. В любой системе счисления цифры служат для
- 4. Виды систем счисленияУнарные системыНепозиционные системыПозиционные системы
- 5. Простейшая и самая древняя система – так
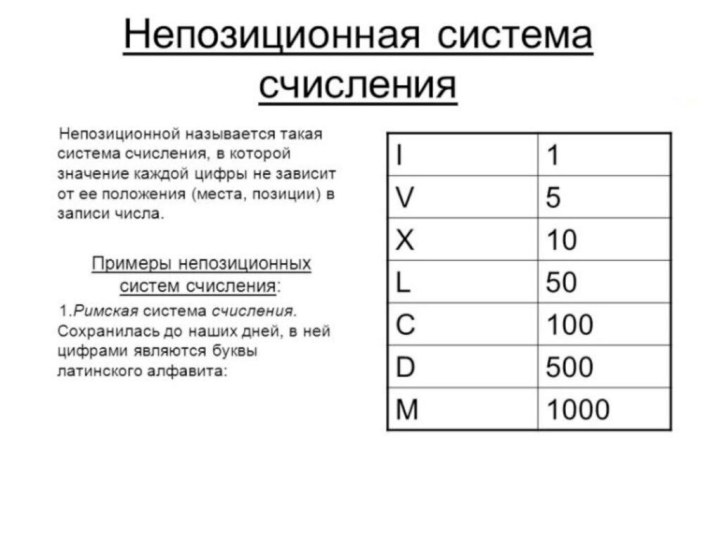
- 7. Система счисления называется непозиционной, если количественный эквивалент
- 9. Система счисления называется позиционной, если количественный эквивалент
- 10. В позиционной системе счисления основными понятиями являются
- 11. Количество цифр, составляющих алфавит, называется его мощностью.В позиционных
- 12. Виды систем счисленияВ компьютерах принято использовать 4 основные системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную.
- 13. Десятичная система счисления – в настоящее время
- 14. В вычислительных машинах используется двоичная система счисления,
- 15. В 16-теричной первые 10 цифр общие, а
- 16. Правила перевода чисел из одной системы счисления
- 17. 1100110112 101110110012 1010111010012 101111101111012 10001101102 11001001112 10111100010112 10011101000111012
- 18. Правило перевода из десятичной системы счисления в
- 19. Чтобы перевести число из двоичной системы в
- 20. Число 100101101112 перевести в восьмеричную и в шестнадцатеричную системы счисления.
- 21. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное
- 22. Скачать презентацию
- 23. Похожие презентации
Система счисления – это знаковая система, в которой приняты определённые правила записи чисел. Знаки, при помощи которых записываются числа называются цифрами, а их совокупность – алфавитом системы счисления.




















Слайд 3 В любой системе счисления цифры служат для обозначения
чисел, называемых узловыми;
остальные числа (алгоритмические) получаются в результате
каких-либо операций из узловых чисел.Слайд 5 Простейшая и самая древняя система – так называемая
унарная система счисления. В ней для записи любых чисел
используется всего один символ – палочка, узелок, зарубка, камушек.Слайд 7 Система счисления называется непозиционной, если количественный эквивалент цифры
в числе не зависит от её положения в записи
числа.Слайд 9 Система счисления называется позиционной, если количественный эквивалент цифры
в числе зависит от её положения в записи числа.
Слайд 10 В позиционной системе счисления основными понятиями являются понятие
алфавита и основания системы счисления.
Алфавитом системы счисления называется совокупность всех
цифр.Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: 7810, 11000102, AF1216 и т. д.
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Слайд 11
Количество цифр, составляющих алфавит, называется его мощностью.
В позиционных системах
счисления один и тот же числовой знак (цифра) в
записи числа имеет различные значения в зависимости от того места(разряда), где он расположен. Разряд - номер позиции в числе. Нумеруются справа налево, начиная с нуля.Пример. Число 618410 запишется в форме многочлена следующим образом:
618410 = 6*10 3 +1*10 2 +8*10 1 +4*10 0
Слайд 12
Виды систем счисления
В компьютерах принято использовать 4 основные
системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную.
Слайд 13 Десятичная система счисления – в настоящее время наиболее
известная и используемая. Древнее изображение десятичных цифр не случайно:
каждая цифра обозначает число по количеству углов в ней. Например, 0 - углов нет, 1 - один угол, 2 - два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
Слайд 14 В вычислительных машинах используется двоичная система счисления, её
основание - число 2. Для записи чисел в этой
системе используют только две цифры - 0 и 1. Двоичная система счисления была придумана математиками и философами задолго до появления компьютеров, еще в ХVII - ХIХ веках.Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной - восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр.
Слайд 15
В 16-теричной первые 10 цифр общие, а дальше
используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному
числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост.Слайд 16 Правила перевода чисел из одной системы счисления в
другую
При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в
десятичную надо это число представить в виде суммы степеней основания его системы счисления.Числа 101001102 , 7038 , 23FA116 перевести в десятичную систему счисления.
101001102=1*27+0*26+1*25+0*24+0*23+1*22+1*21+0*20=128+32+4+2=16610
7038=7*82+0*81+3*80=448+3=44710
23FA116=2*164+3*163+15*162+10*161+1*160=131072+12288+3840+160+1=147361
Слайд 17
1100110112
101110110012
1010111010012
101111101111012
10001101102
11001001112
10111100010112
10011101000111012
Слайд 18 Правило перевода из десятичной системы счисления в систему
с основанием q:
Последовательно выполнять деление исходного числа и получаемых
частных на q до тех пор, пока не получим частное, меньшее делителя.Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
Слайд 19
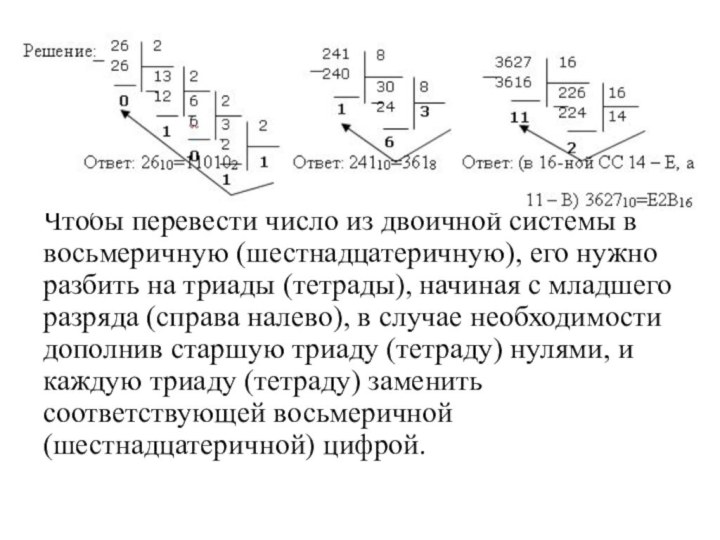
Чтобы перевести число из двоичной системы в восьмеричную
(шестнадцатеричную), его нужно разбить на триады (тетрады), начиная с
младшего разряда (справа налево), в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду (тетраду) заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.Слайд 21 Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо
каждую цифру заменить эквивалентной ей двоичной триадой (тетрадой).
Числа 7268 и
74С16 перевести в двоичную систему счисления.7268= 111 010 1102
74С16 = 0111 0100 11002 (при записи числа первый 0 не пишется)