Слайд 2
В математике рекурсия
имеет отношение к методу определения функций и числовых
рядов: рекурсивно заданная функция определяет своё значение через обращение к себе самой
с другими аргументами.
Конечная рекурсивная функция.
Здесь каждое следующее рекурсивное обращение делается с аргументом, меньшим на единицу. Поскольку n, по определению, целое неотрицательное число, через n рекурсивных обращений вычисление функции гарантированно придёт к частному случаю , на котором рекурсия прекратится.
Слайд 3
В математике рекурсия
Бесконечная рекурсивная функция.
Примером может служить один
из вариантов разложения числа Эйлера:
Подобным образом могут задаваться бесконечные ряды,
бесконечные непрерывные дроби и так далее.
Слайд 6
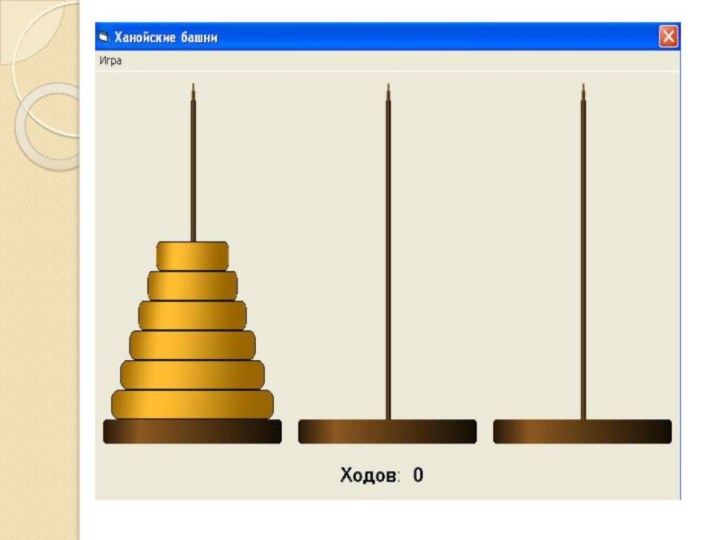
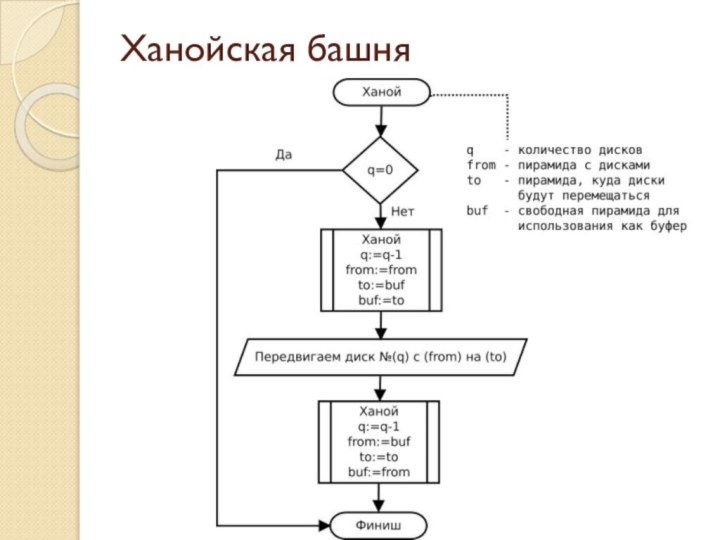
Ханойская башня
//n – количество дисков
//a, b, c –
номера штырьков. Перекладывание производится со штырька a,
//на штырек
b при вспомогательном штырьке c.
procedure Hanoi(n, a, b, c: integer);
begin
if n > 1 then
begin
Hanoi(n-1, a, c, b);
writeln(a, ' -> ', b);
Hanoi(n-1, c, b, a);
end else
writeln(a, ' -> ', b);
end;
Слайд 7
В программировании рекурсия —
вызов функции (процедуры) из неё же самой, непосредственно (простая
рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция А вызывает
функцию В, а функция А — функцию В .
Количество вложенных вызовов функции или процедуры называется глубиной рекурсии. Рекурсивная программа позволяет описать повторяющееся или даже потенциально бесконечное вычисление, причём без явных повторений частей программы и использования циклов.
Слайд 8
Структурно рекурсивная функция на верхнем уровне всегда представляет
собой команду ветвления (выбор одной из двух или более
альтернатив в зависимости от условия (условий), которое в данном случае уместно назвать «условием прекращения рекурсии»), имеющей две или более альтернативные ветви, из которых хотя бы одна является рекурсивной и хотя бы одна — терминальной. Рекурсивная ветвь выполняется, когда условие прекращения рекурсии ложно, и содержит хотя бы один рекурсивный вызов — прямой или опосредованный вызов функцией самой себя.
Слайд 9
Пример рекурсивной процедуры:
procedure Rec(a: integer);
begin
if a>0 then
Rec(a-1);
writeln(a);
end;
Слайд 10
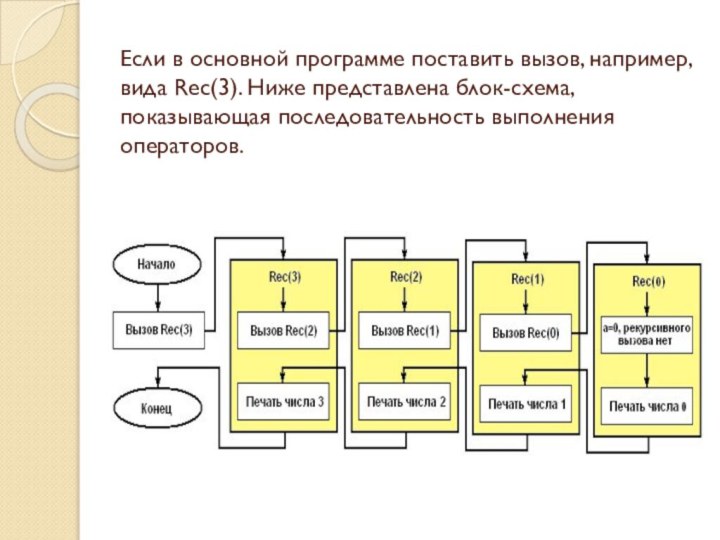
Если в основной программе поставить вызов, например, вида
Rec(3). Ниже представлена блок-схема, показывающая последовательность выполнения операторов.
Слайд 11
Процедура Rec вызывается с параметром a = 3.
В ней содержится вызов процедуры Rec с параметром a
= 2. Предыдущий вызов еще не завершился, поэтому можете представить себе, что создается еще одна процедура и до окончания ее работы первая свою работу не заканчивает. Процесс вызова заканчивается, когда параметр a = 0. В этот момент одновременно выполняются 4 экземпляра процедуры. Количество одновременно выполняемых процедур называют глубиной рекурсии.
Четвертая вызванная процедура (Rec(0)) напечатает число 0 и закончит свою работу. После этого управление возвращается к процедуре, которая ее вызвала (Rec(1)) и печатается число 1. И так далее пока не завершатся все процедуры. Результатом исходного вызова будет печать четырех чисел: 0, 1, 2, 3.
Слайд 12
В качестве самостоятельного упражнения подумайте, что получится при
вызове Rec(4). Также подумайте, что получится при вызове описанной
ниже процедуры Rec2(4), где операторы поменялись местами.
procedure Rec2(a: integer);
begin
writeln(a);
if a>0 then
Rec2(a-1);
end;
Обратите внимание, что в приведенных примерах рекурсивный вызов стоит внутри условного оператора. Это необходимое условие для того, чтобы рекурсия когда-нибудь закончилась. Также обратите внимание, что сама себя процедура вызывает с другим параметром, не таким, с каким была вызвана она сама. Если в процедуре не используются глобальные переменные, то это также необходимо, чтобы рекурсия не продолжалась до бесконечности.