Презентация на тему по информатике на тему Основы алгоритмитизации

задачи.

Слово «алгоритм» происходит от Algorithmi – латинской формы написания

имени великого среднеазиатского математика IX века Мухаммеда–аль–Хорезми (787 – 850), который сформулировал правила выполнения арифметических действий.

Налить в кастрюлю воду.
Включить плиту.
Поставить кастрюлю на плиту.
Ждать, пока вода закипит.
Засыпать в кастрюлю крупу.
Посолить.
Варить 10 минут.
Выключить плиту.

Пример 1

Пример 2

Пример 3

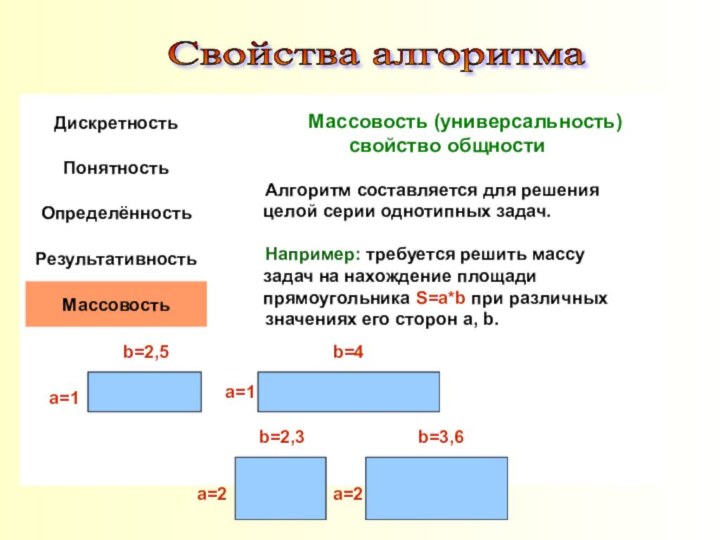
Определение алгоритма

задачи.
Встретить Красную шапочку.
Спросить ее, куда она идет.
Добежать до домика

бабушки.
Съесть бабушку.
Лечь в бабушкину кровать.
Дождаться прихода Красной шапочки.
Ответить на вопросы Красной шапочки.
Попытаться съесть Красную шапочку.

Пример 1

Пример 2

Пример 3

Определение алгоритма

примеры алгоритмов:
кулинарный рецепт;
инструкция по сборке машинки из
деталей детского конструктора;
инструкция

по использованию
стиральной машины;
«алгоритм покупки хлеба»;
и т.д.

Пример 1

Пример 2

Пример 3

Определение алгоритма

команда «Умножить» не будет понята и выполнена исполнителем.
Исполнители алгоритма

Исполнитель – это человек или устройство, для управления которым составлен алгоритм. В качестве исполнителей часто выступают животные. (на арене цирка)
Система команд исполнителя (СКИ) – это набор действий, т.е. команд, которые умеет выполнять исполнитель.
Если алгоритм составлен для исполнителя правильно, то он достигает поставленной цели.

быть разбит на последовательность отдельно выполняемых шагов.

Пример:
Алгоритм приготовления блюда
быстрого

питания:
Шаг 1. Высыпать в емкость содержимое пакетика.
Шаг 2. Налить в емкость 200 мл горячей воды.
Шаг 3. Тщательно перемешать.

Дискретность

Понятность

Определённость

Результативность

Массовость

Свойства алгоритма

Блок-схема

только команды, входящие в СКИ.

У каждого исполнителя имеется
свой

перечень команд, которые
он может исполнить.
СКИ – система команд
исполнителя
Пример:
Инженер может выполнить
свою работу. Повар не может
выполнить работу инженера,
даже если ему дана подробная
инструкция.

Дискретность

Понятность

Определённость

Результативность

Массовость

Свойства алгоритма

чёткое однозначное действие исполнителя.

Пример неточной команды:
«Рецепт» для исполнителя
повара,

команда: «Положить
несколько ложек сахара».
Непонятно, сколько ложек, каких
ложек (столовых, чайных).
Каждый повар может понять это
по-разному, и результаты будут
разными.
Правильно:
«Положить 4 столовые ложки сахара»
«Налить 1 стакан молока»

Массовость

Свойства алгоритма

число шагов.

Бесконечно исполняемый
алгоритм не может привести к
результату.

Пример

бесконечной команды:
Маршрут «Кольцо». Команда:
«Ехать по кольцевой дороге,
пока она не закончится».

Массовость

Свойства алгоритма

составляется для решения целой серии однотипных задач.

Например: требуется решить

массу задач на нахождение площади прямоугольника S=a*b при различных
значениях его сторон a, b.

Дискретность

Понятность

Определённость

Результативность

Массовость

Свойства алгоритма

a=1

b=2,5

a=1

b=4

a=2

a=2

b=2,3

b=3,6

– термины, псевдокоды
На графическом языке – блок-схема
На языке программирования
Способы

записи алгоритмов

графической записи алгоритмов установлен государственный стандарт. Причём любое действие

изображается с помощью геометрических фигур или блоков, связанных между собой стрелками.

Начало, конец алгоритма

Ввод (вывод) данных

Начало цикла (повторение)

Выбор способа решения

Вывод результатов на принтер

на 3
Задание:
Составить для исполнителя алгоритм в виде блок-схемы получения

числа 24 из числа 3.

Алгоритм, в котором команды записываются в строго четкой последовательности, называют линейным.

Пояснение: начальное значение А=3, дальше значение А будет меняться, т.к. выполняется вычислительное действие, поэтому записано:
A:=A*2 (знак «:=» присвоить вычислительное действие,
«*» - умножить)

Блок-схема

Расчёт

(1777-855)
придумал алгоритм быстрого сложения чисел
от 1 до

100.
(Количество чисел должно быть чётным числом)
Алгоритм (на естественном языке)
Подсчитать количество чисел в последовательности от 1 до 100. (100)
Найти количество пар чисел. (100/2=50)
Сложить первое и последнее числа. (1+100=101)
Умножить количество полученных пар чисел на получившуюся сумму. (50*101=5050)

начало

N1=1;
Nk=100;
K=100

P:=K/2

S:=N1+Nk

конец

S:=P*S

S

Блок-схема

Расчёт

Пояснение: знак «*» - умножить, «/» - разделить.

!