- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по информатике. Программирование. Приближенные методы решения уравнений. Метод простой итерации.
Содержание
- 2. Вопросы для повторения:Что значит решить уравнение f(x)=0? Дайте определение корня уравнения?Объясните геометрический смысл корня?
- 4. Вопросы для повторения:В каких случаях мы прибегаем
- 6. Вопросы для повторения:Теорема 1 о существовании корня
- 7. Вопросы для повторения:Из каких этапов состоит процесс
- 8. ПОСТАНОВКА ЗАДАЧИ:Пусть дано уравнение f(x) =0,
- 9. ПОСТАНОВКА ЗАДАЧИ:Возможны два случая: 1. Последовательность
- 10. Теорема о сходимости итерационного процессаПусть на
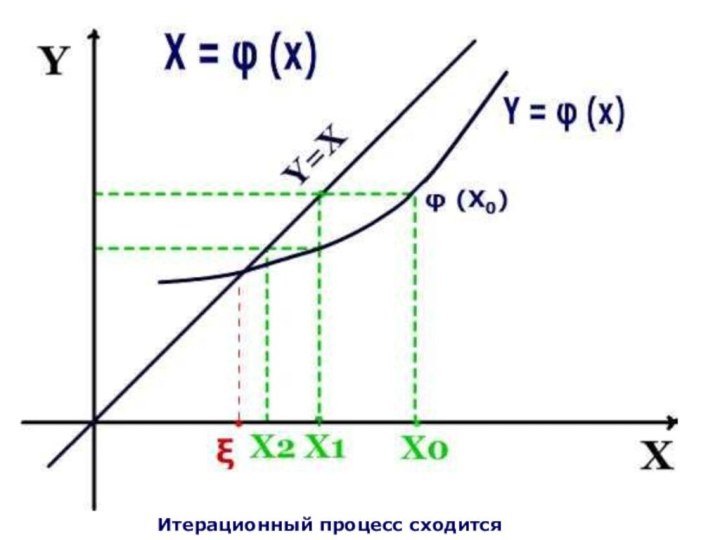
- 11. Итерационный процесс сходится
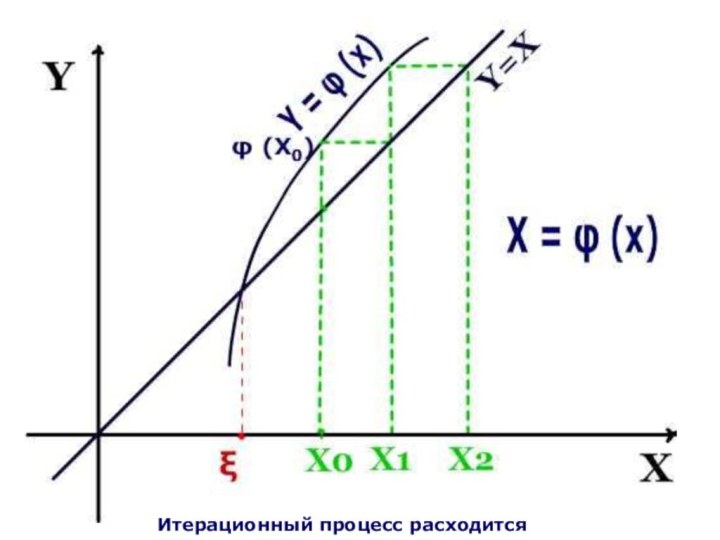
- 12. Итерационный процесс расходится
- 13. Точность приближенияПусть ξ точное значение корня уравнения
- 14. Замечание:Уравнение f(X) =0 привести к виду
- 15. Описание данных в программеVar
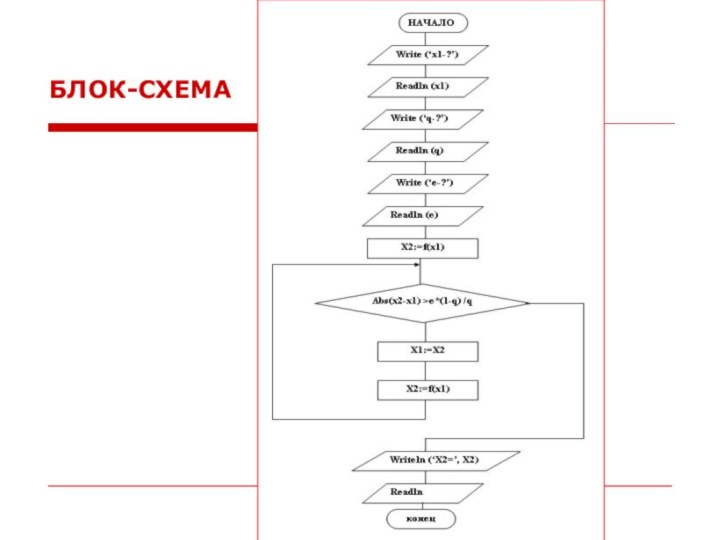
- 16. БЛОК-СХЕМА
- 17. ДАННЫЕ ДЛЯ ТЕСТИРОВАНИЯ
- 18. Скачать презентацию
- 19. Похожие презентации
Вопросы для повторения:Что значит решить уравнение f(x)=0? Дайте определение корня уравнения?Объясните геометрический смысл корня?







![Презентация по информатике. Программирование. Приближенные методы решения уравнений. Метод простой итерации. Теорема о сходимости итерационного процессаПусть на отрезке [a,b] имеется единственный](/img/tmb/7/616139/ab1e8a3c5721188443b66231a46303e0-720x.jpg)





Слайд 2
Вопросы
для повторения:
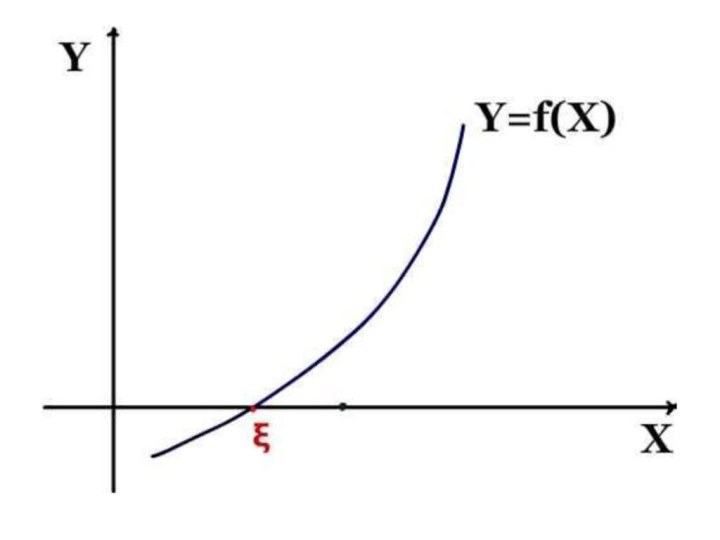
Что значит решить уравнение f(x)=0?
Дайте определение
корня уравнения?
Слайд 4
Вопросы
для повторения:
В каких случаях мы прибегаем к численным
методам решения уравнений?
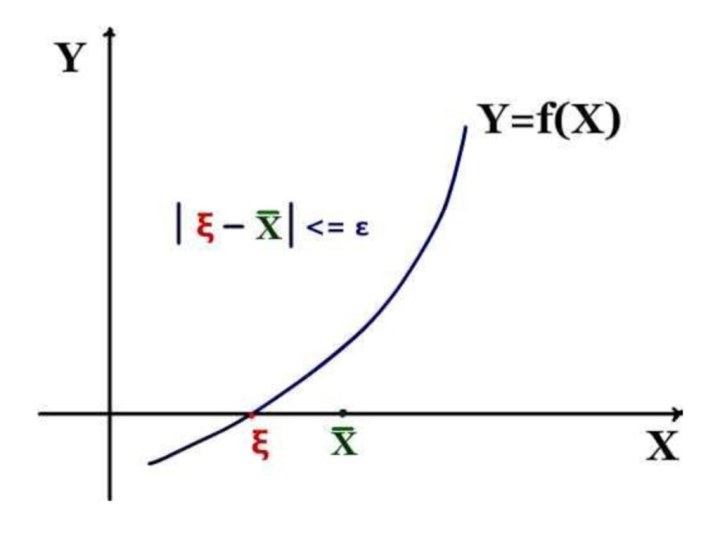
Что значит корень вычислен с заданной
степенью точности ε ?
Слайд 6
Вопросы
для повторения:
Теорема 1 о существовании корня на отрезке?
Необходимое условие существования корня.
Теорема 2 о существовании корня
на отрезке? Необходимое и достаточное условие существования корня. Теорема 3 о существовании корня на отрезке?
Слайд 7
Вопросы
для повторения:
Из каких этапов состоит процесс нахождения корней
приближенными (численными) методами?
Что значит отделить корни?
Когда корень
считается отделённым на отрезке?
Слайд 8
ПОСТАНОВКА
ЗАДАЧИ:
Пусть дано уравнение f(x) =0, где f(x)
- непрерывная функция.
Требуется определить вещественный корень этого уравнения,
заключенный на отрезке [a,b].Заменим уравнение f(x) =0
равносильным ему уравнением X = φ (x) (1)
Выберем каким-либо способом X0 є [a,b]
и подставим его в правую часть уравнения (1); тогда получим X1= φ (X0)
Затем это значение X1 подставим снова в правую часть уравнения (1) и получим X2= φ (X1)
Повторяя этот процесс, получим последовательность чисел Xn= φ (Xn-1)
Слайд 9
ПОСТАНОВКА
ЗАДАЧИ:
Возможны два случая:
1. Последовательность X0, X1,
X2, …, Xn, … сходится, т.е. имеет предел, и
тогда этот предел будет корнем уравненияf(x) =0;
lim Xn =ξ n → ∞
2. Последовательность X0, X1, X2, …, Xn, … расходится, т.е. не имеет предела.
Слайд 10
Теорема
о сходимости итерационного процесса
Пусть на отрезке [a,b]
имеется единственный корень уравнения X = φ (X).
Если
во всех точках этого отрезка производная φ ’(X) удовлетворяет неравенству |φ ’ (X)| <=q <1Если при этом выполняется условие a<=φ (X)<=b , то итерационный процесс сходится, а за первое приближение можно взять любое число из отрезка [a,b].
Последнее условие означает, что все приближения X0, X1, X2, …, Xn, … находятся на отрезке [a,b].
Чем меньше |φ ’ (X)|, тем лучше сходится итерационный процесс.
Слайд 13
Точность
приближения
Пусть ξ точное значение корня уравнения X =
φ (X) ,
а число q определяется из соотношения
|φ
’ (X)| <=q <1
(Практически q можно получить как верхнюю границу модуля производной | φ’ (x)| при X є [a,b]) Тогда справедливо соотношение
| ξ – Xn |<=q/(1-q) |Xn- Xn-1|
Если поставить условие, что истинное значение корня должно отличаться от приближенного значения на величину ε , т. е. | ξ – Xn |<= ε , то приближения
X0, X1, X2, …, Xn, … надо вычислять до тех пор, пока не будет выполнено неравенство:
q/(1-q) |Xn- Xn-1| <= ε
или |Xn- Xn-1|<= ε (1-q)/q